北师大版八年级数学下册 图形的平移与旋转回顾与思考_(2)（教案）

图形的平移与旋转 回顾与思考

【学习任务分析】

（一）知识与技能

1．复习平移、旋转与中心对称的概念和性质。掌握坐标系中平移、对称的坐标特征。

2．灵活运用平移、旋转与中心对称的概念和性质解决相关图形问题。

（二）过程与方法

经历复习本章的知识，培养梳理知识的能力，核心知识的理解是关键。

（三）情感、态度与价值观

1．经历对生活中的典型图案进行观察、分析、欣赏等过程，进一步发展空间观念、增强审美意识。

2．通过学生之间的交流、讨论、培养学生的合作精神。

【教学重点】

理解平移、旋转与中心对称的概念和性质。掌握坐标系中平移、对称的坐标特征。

【教学难点】

灵活运用平移、旋转与中心对称的概念和性质解决相关图形问题。

【教学过程】

分为以下几个环节：回顾知识、探究学习、应用提升、总结归纳。

（一）回顾知识

1． 知识点归纳：

（1）平移的概念：在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做图形的平移。

平移的性质：平移不改变图形的形状和大小；图形经过平移，连接各组对应点所得的线段互相平行且相等。

（2）旋转的概念：把一个图形绕一个定点转动一定的角度，这样的图形运动叫做旋转，这个定点叫做旋转中心，旋转的角度叫做旋转角。

旋转的性质：旋转前、后的图形全等；对应点到旋转中心的距离相等；每一对对应点与旋转中心的连线所成的角彼此相等。

（3）中心对称：如果把一个图形绕着某一点旋转180°，能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做它们的对称中心。

中心对称图形：把一个图形绕某个点旋转180°，如果旋转后的图形与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。

性质：成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分。

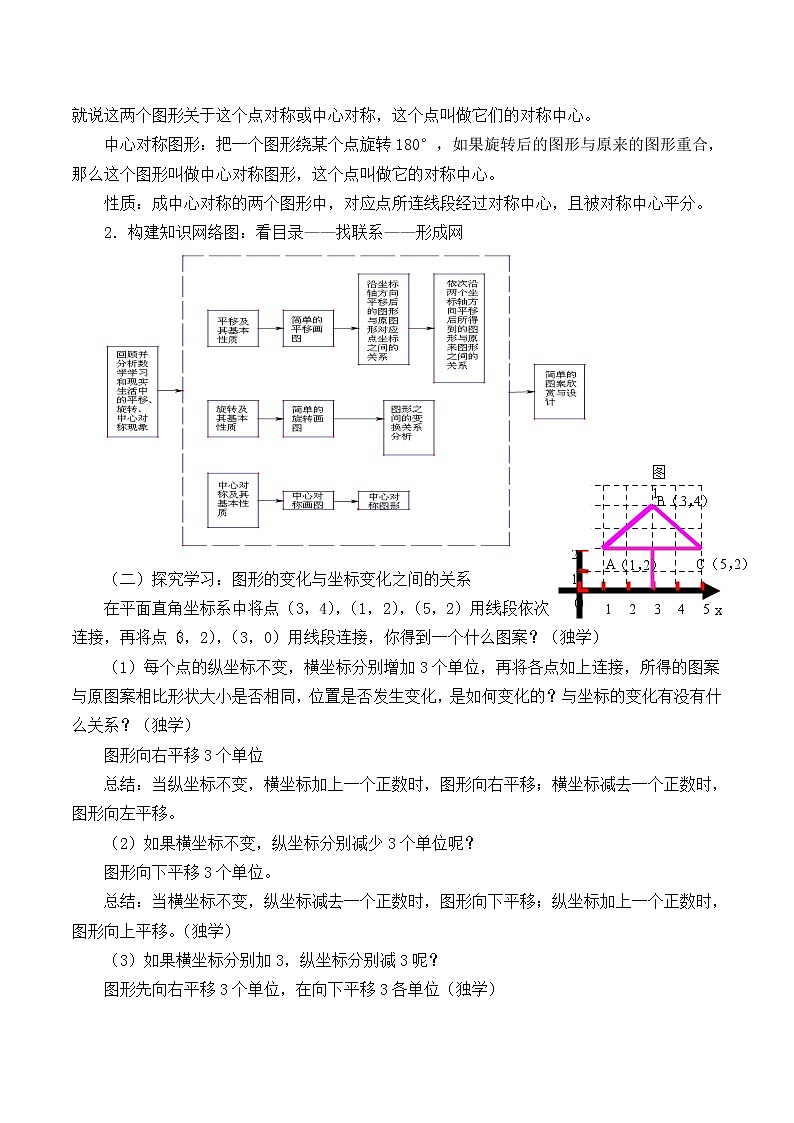
2．构建知识网络图：看目录——找联系——形成网

（二）探究学习：图形的变化与坐标变化之间的关系

在平面直角坐标系中将点（3，4），（1，2），（5，2）用线段依次连接，再将点（3，2），（3，0）用线段连接，你得到一个什么图案？（独学）

（1）每个点的纵坐标不变，横坐标分别增加3个单位，再将各点如上连接，所得的图案与原图案相比形状大小是否相同，位置是否发生变化，是如何变化的？与坐标的变化有没有什么关系？（独学）

图形向右平移3个单位

总结：当纵坐标不变，横坐标加上一个正数时，图形向右平移；横坐标减去一个正数时，图形向左平移。

（2）如果横坐标不变，纵坐标分别减少3个单位呢？

图形向下平移3个单位。

总结：当横坐标不变，纵坐标减去一个正数时，图形向下平移；纵坐标加上一个正数时，图形向上平移。（独学）

（3）如果横坐标分别加3，纵坐标分别减3呢？

图形先向右平移3个单位，在向下平移3各单位（独学）

能否看成一次平移呢？（群学）

平移的方向是由点（3，4）到点（6，1）的方向，距离是3√2。

（4）如果横坐标不变，纵坐标分别乘-1呢？

横坐标不变，纵坐标相反，则图形关于x轴对称

（5）如果纵坐标不变，横坐标分别乘-1呢？

 纵坐标不变，横坐标相反，则图形关于y轴对称。

（6）如果横、纵坐标分别乘-1呢？

关于原点中心对称。

（三）应用提升：旋转在几何证明中的应用

在正ΔABC中，P为ΔABC内一点，将ΔABP绕A点按逆时针方向旋转600，使得AB与AC重合。经过这样旋转变化，将图（1-1-a）中的PA、PB、PC三条线段集中于图（1-1-b）中的一个ΔP'CP中，请确定ΔP'AP的形状           。

例1、如图：设P是等边ΔABC内的一点，PA=3， PB=4，PC=5，∠APB的度数是________。

（四）巩固练习

1．中考链接（2014宜宾）在平面直角坐标系中，讲点A(-1，2)向右平移3个单位得到点B，则点B关于原点对称点C的的坐标是          。

2．P是正方形内一点，将△ ABP绕点B顺时针方向旋转至与△CBP′重合，若PB=3，求PP′的长。

（五）总结归纳

图形的轴对称、平移、旋转是几何中的重要概念，应用轴对称、平移、旋转解题也是一种极为重要的数学思想方法，适当地应用轴对称、平移、旋转等方法，将那些分散、远离的条件从图形的某一部分转移到适当的新的位置上，集中、汇集已知条件和求证结论，发现、拓展解题思路，构造基础三角形、平行四边形，进行计算与证明。

【作业布置】

课后练习

【教学反思】