资料中包含下列文件,点击文件名可预览资料内容





当前文件暂不支持在线预览,请下载使用
还剩19页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学八年级下册 1.3.1 《线段的垂直平分线(1)》课件+分层练习(含答案解析)
展开
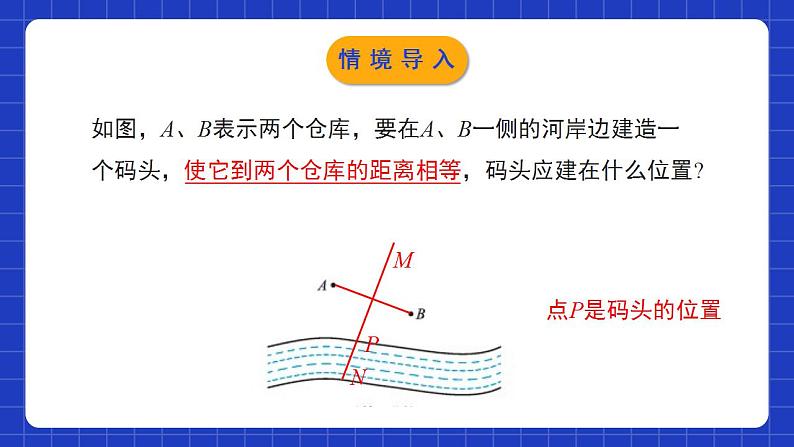
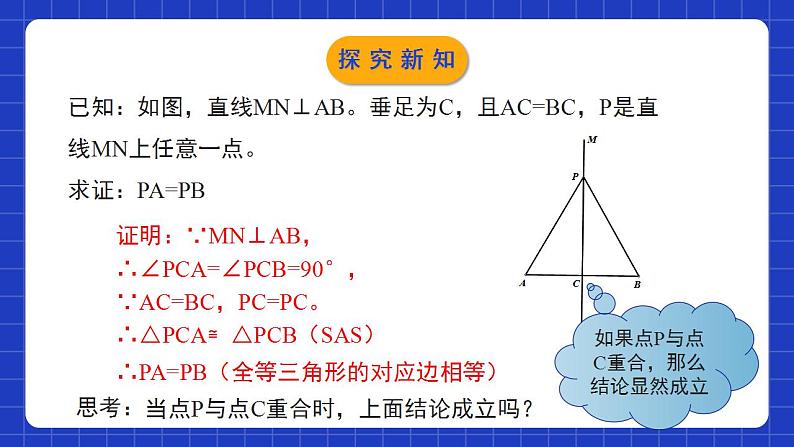
1.3.1线段的垂直平分线(1)学习目标经历利用逻辑推理验证线段垂直平分线的性质及判定的过程,使学生理解逻辑证明的重要性。0102利用线段垂直平分线的性质及判定解决实际问题,培养学生解决问题的能力。(1)线段是轴对称图形吗?它的对称轴是什么?垂直且平分一条线段的直线叫作这条线段的垂直平分线. 线段是轴对称图形,线段的垂直平分线是它的对称轴.(2)什么叫线段的垂直平分线?情境导入如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置? PNM点P是码头的位置情境导入线段垂直平分线的性质 如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.P1A ____P1BP2A ____ P2BP3A ____ P3B===探究新知猜想:点P1,P2,P3,… 到点A 与点B 的距离分别相等. 线段垂直平分线上的点到这条线段两个端点的距离相等.由此你能得到什么结论?探究新知已知:如图,直线MN⊥AB。垂足为C,且AC=BC,P是直线MN上任意一点。求证:PA=PB证明:∵MN⊥AB,∴∠PCA=∠PCB=90°,∵AC=BC,PC=PC。∴△PCA≌△PCB(SAS)∴PA=PB(全等三角形的对应边相等)思考:当点P与点C重合时,上面结论成立吗?如果点P与点C重合,那么结论显然成立探究新知归纳总结线段垂直平分线的性质定理:PABMCN线段垂直平分线上的点到这条线段两个端点的距离相等.条件:点在线段的垂直平分线上;结论:这个点到线段两端点的距离相等.几何语言:∵MN⊥AB,AC=BC,点P在MN上, ∴PA=PB. 作用:可用来证明两线段相等.探究新知解:AB=AC=CE,AB+BD=DE.理由如下:∵AD⊥BC,BD=DC, ∴AB=AC.∵点C在AE的垂直平分线上, ∴AC=CE.∴AB=AC=CE,AB+BD=CE+DC=DE,即AB+BD=DE.例:如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上, AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?探究新知线段垂直平分线的判定1.经过线段的中点,并且垂直于这条线段的直线是线段的垂直平分线。2.思考:线段的垂直平分线有哪些判定方法?(定义判定)你能写出垂直平分线性质定理的逆命题吗??性质定理的逆命题?探究新知性质定理(原命题):如果一个点是线段垂直平分线上的点,那么这个点到这条线段两个端点的距离相等。逆命题:如果一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上。这个逆命题是真命题吗?你能证明它吗?探究新知已知:线段AB和点P,PA=PB,求证:点P在线段AB的垂直平分线上.证明:①若点P在线段AB上,则点P为线段AB中点,结论显然成立.②若点P不在AB上,取AB中点M,连接PM .∵PA=PB,AM=BM,∴PM⊥AB(等腰三角形三线合一).综上所述,原命题成立.探究新知归纳总结到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.线段垂直平分线的判定定理:条件:点到线段两端点距离相等;结论:点在线段垂直平分线上.几何语言:∵PA=PB, ∴点P在线段AB的垂直平分线上.作用:①作线段的垂直平分线的依据; ②可用来证线段垂直、相等.探究新知定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理:到一条条线段两个端点距离相等的点,在这条线段的垂直平分线上.互为逆定理综上:线段的垂直平分线是到线段两个端点距离相等的所有点的集合.探究新知例2:已知:如图△ABC中,AB=AC,O是△ABC内一点,且OB=OC.求证:直线AO垂直平分线段BC.证明:∵AB=AC, ∴A在线段BC的垂直平分线(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).同理,点O在线段BC的垂直平分线.∴直线AO是线段BC的垂直平分线(两点确定一条直线).探究新知例2:已知:如图△ABC中,AB=AC,O是△ABC内一点,且OB=OC.求证:直线AO垂直平分线段BC.证明:延长AO交BC于点D,∵AB=AC, AO=AO, OB=OC ,∴△ABO≌△ACO(SSS).∴∠BAO=∠CAO,∵AB=AC,∴AO⊥BC.∵OB=OC ,OD=OD ,∴RT△DBO≌RT△DCO(HL).∴BD=CD.∴直线AO垂直平分线段BC.探究新知1.如图,直线PO与AB交于点O,PA=PB,则下列结论中正确的是( )A.AO=BOB.PO⊥ABC.PO是AB的垂直平分线D.P点在AB的垂直平分线上D随堂练习2.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D.若ED=5,则CE的长为( )A.7B.8C.10D.12C随堂练习3.如图,AB=AD,则添加一个条件_________,即可得到AC是BD的垂直平分线.CB=CD随堂练习4.如图,CD是AB的垂直平分线,垂足为D.(1)AD=________,∠ADC=________°,AC=________;(2)若AD=3,AC=5,则△ABC的周长为________.BD90BC16随堂练习5.如图,AB是线段CD的垂直平分线,E,F是AB上的两点.求证:∠ECF=∠EDF.证明:∵E,F是线段CD的垂直平分线AB上两点∴EC=ED,FC=FD∴∠ECD=∠EDC,∠FCD=∠FDC∴∠ECD+∠FCD=∠EDC+∠FDC,即∠ECF=∠EDF随堂练习6.如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F,连接AF,求∠AFC的度数.解:∵AB=AC,∠BAC=120°,∴∠B=∠C=(180°-120°)÷2=30°.∵EF垂直平分AB,∴BF=AF.∴∠BAF=∠B=30°.∵∠AFC为△ABF的外角,∴∠AFC=∠BAF+∠B=30°+30°=60°.随堂练习7.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线分别交AB、AC于点D、E.求∠EBC的度数.解:∵AB=AC,∠A=40°,∴∠ABC=∠C=(180°-40°)÷2=70°.∵DE垂直平分AB,∴AE=BE.∴∠ABE=∠A=40°.∴∠EBC=∠ABC-∠ABE=70°-40°=30°.随堂练习8.如图,在Rt△ABC中,∠C=90°,∠A=15°,MN垂直平分AB,交AB于点M,交AC于点N,AN=8,连接BN.(1)求∠BNC的度数;(2)求BC的长.解:(1)∵MN垂直平分AB,∴AN=BN.∴∠ABN=∠A.∵∠A=15°,∴∠ABN=15°.∵∠BNC是△ABN的外角,∴∠BNC=∠ABN+∠A=15°+15°=30°.随堂练习8.如图,在Rt△ABC中,∠C=90°,∠A=15°,MN垂直平分AB,交AB于点M,交AC于点N,AN=8,连接BN.(1)求∠BNC的度数;(2)求BC的长.随堂练习1.经过线段的中点,并且垂直于这条线段的直线是线段的垂直平分线。2.到一条线段两个端点距离相等的点, 在这条线段的垂直平分线上。1.垂直、平分2.线段垂直平分线上的点到这条线段两端的距离相等。线段的垂直平分线性质判定课堂小结课程结束
相关资料
更多









