第1章 解直角三角形 章末复习与小结 浙教版九年级数学下册教学课件

这是一份第1章 解直角三角形 章末复习与小结 浙教版九年级数学下册教学课件，共25页。

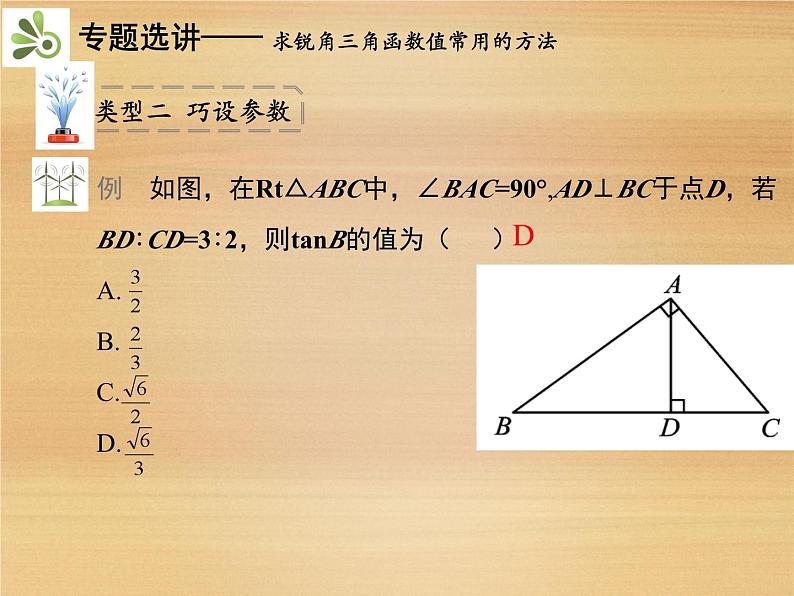
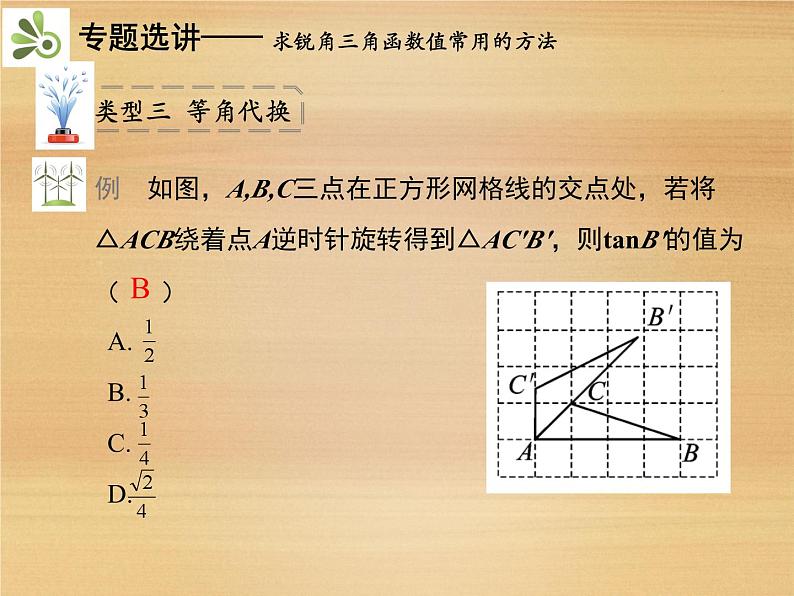
直角三角形中的边角关系锐角三角函数解直角三角形实际问题方法专题15 求锐角三角函数值常用的方法 P144方法专题16 巧用锐角三角函数解决实际问题 P154解：∵在Rt△ABC中，∴AC=12,DBBCA解：延长HF交CD于点N，延长FH交AB于点M，由题意可得MB=HG=FE=ND=1.6 m，HF=GE=8 m，MF=BE，HN=GD，MN=BD=24 m.∵AB=CD，∴AB-BM=CD-ND，即AM=CN.答：教学楼AB的高度约为13.3 m.设AM=CN=x m.在Rt△AFM中，∠AFM=45°,∴MF=AM=x m.在Rt△CNH中，∠CHN=30°，∵HF=MF+HN-MN=8 m，解得x≈11.7，∴AM≈11.7 m.∴AB=AM+BM=11.7+1.6=13.3（m）.20C（1分）（2分）（3分）（4分）解：（1）过点A作AE⊥BC于点E．∴CE=AC·cosC=1，在Rt△ABE中，∴BE=3AE=3.∴BC=BE+CE=3+1=4.（6分）（8分）（2）∵AD是△ABC的中线，∴DE=CD-CE=2-1=1.∵AE=1,∴DE=AE.又∵AE⊥BC，∴∠ADC=45°，