


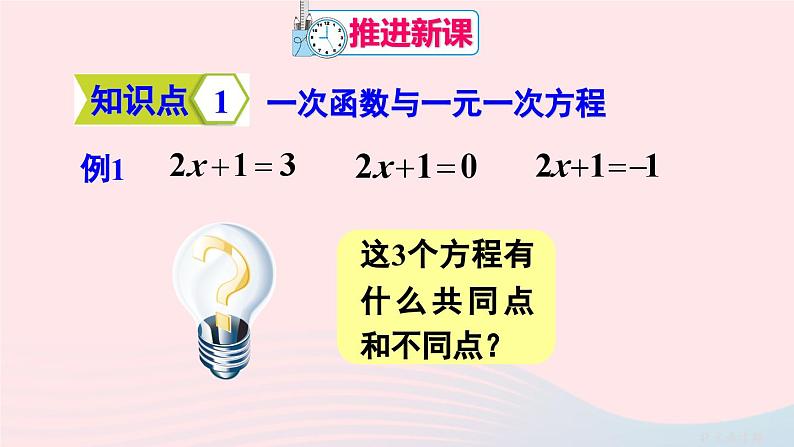



初中数学人教版八年级下册19.2.3一次函数与方程、不等式背景图ppt课件
展开数学知识之间是相互联系的,一次函数知识并不是孤立的,其实它与以前我们学过的有关知识有密切联系.今天我们来探讨一次函数与方程、不等式之间的联系.
(1)会从函数的角度看方程(组)解的意义.
(2)会从函数的角度看不等式的解集的意义.
(3)会将函数问题转化为解方程(组)或不等式(组)问题.
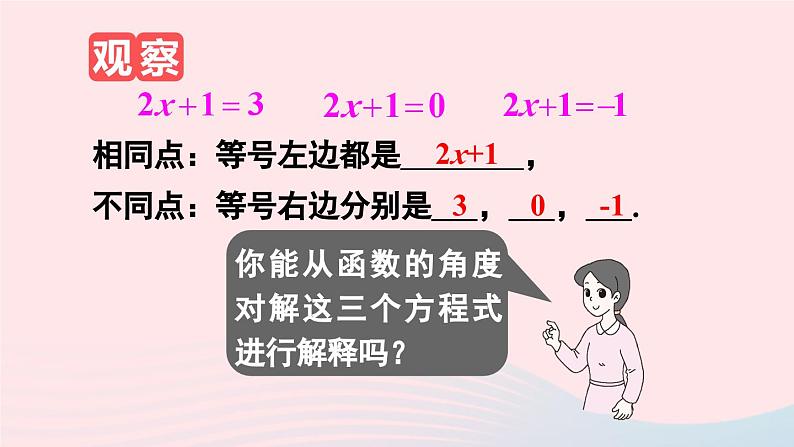
相同点:等号左边都是 ,
不同点:等号右边分别是 , , .
从函数的角度看,解这三个方程
方程2x+1=3的解是: ;即当 时,函数y=2x+1的值为3,也就是 ;
方程2x+1=-1的解是: ;即当 时,函数y=2x+1的值为-1,也就是 .
方程2x+1=0的解是: ;即当 时,函数y=2x+1的值为0,也就是 ;
从函数的角度看,解这3个方程相当于在一次函数y=2x+1的函数值分别为3,0,-1时,求自变量x的值.
因为任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0)的形式,所以解一元一次方程相当于在某个一次函数y=ax+b(a≠0)的函数值为0时,求自变量x的值.
1.直线y=2x+b与x轴的交点坐标为(2,0),则关于x的方程2x+b=0的解是x= .
2.若直线y=kx+6与两坐标轴所围成的面积是24,求常数k的值.
解:设直线y=kx+6与x轴和y轴分别交于点A、B.
令x=0,得y= 6,
相同点:不等号左边都是 ,
不同点:不等号右边分别是 , , .
不等式3x+2>2的解是: ;即当 时,函数 ;
不等式3x+2<-1的解是: ;即当 时,函数 .
不等式3x+2<0的解是: ;即当 时,函数 ;
从函数的角度看,解这3个不等式相当于在一次函数y=3x+2的函数值分别满足大于2、小于0、小于-1的点时,求自变量x的取值范围.
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.
在直角坐标系中,直线y=kx+3(k≠0)过点(2,2),且与x轴、y轴分别交于A、B两点,求不等式kx+3≤0的解集.
解:∵直线y=kx+3(k≠0)过点(2,2),
∴不等式kx+3≤0的解集为x≥6.
例3 1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系;
(1)气球上升时间满足 .
1号气球的函数解析式为 ;
2号气球的函数解析式为 .
(2)在某个时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
(2)在某个时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.则只需求出x和y的值.
容易想到解二元一次方程组:
这就是说,当上升20min时,两个气球都位于海拔25m的高度.
一般地,因为每个含有未知数x和y的二元一次方程,都可以改写为( )的形式,所以每个这样的方程都对应一个一次函数,于是也对应 .这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解.
从“数”的角度看:解二元一次方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少; 从“形”的角度看:解二元一次方程组,相当于确定两条直线的交点坐标.因此,我们可以用画一次函数图象的方法得到方程组的解.
考虑下面两种移动电话计费方式:
用函数方法解答何时两种计费方式费用相等.
解:设通话时间为x分,若按“方式一”计费方式,则收取费用y=30+0.3x;若按“方式二”计费方式收取费用,则收取费用y=0.4x.在同一直角坐标系中分别画出这两个函数的图象,如下图:
所以两图象交于点(300,120),
当x=300时,30+0.3x=0.4x,
即当一个月内通话时间等于300分钟时,选择两种计费方式费用相等.
误 区 诊 断
已知直线y=-2x-1与直线y=3x+m相交于第三象限,求m得取值范围.
错因分析:两条直线相交于第三象限并不代表直线y=kx+b中的b<0.应先求出用含m的式子表示的交点坐标,再求m的取值范围.
1.已知直线y=ax-b的图象如图所示,则关于x的方程ax-b=0的解为x= ,当x=0时,y= .
4.函数y=2x+6的图象如图,利用图象:
(1)求方程2x+6=0的解;
由图象可得:图象过点(-3,0).∴方程2x+6=0的解为x=-3;
(2)求不等式2x+6>0的解集;
由图象可得:当x>-3时,函数y=2x+6的图象在x轴上方.∴不等式2x+6>0的解集为x>-3;
(3)若-1≤y≤3,求x的取值范围.
由图象可得:函数图象过F(-1.5,3),G(-3.5,-1)两点,当-3.5≤x≤-1.5时,函数y=2x+6的函数值满足-1≤y≤3,∴x的取值范围是-3.5≤x≤-1.5.
5.已知一次函数y=kx+b(k、b为常数,且k≠0)的图象(如图①).
(1)方程kx+b=0的解为 ,不等式kx+b<4的解集为 ;
(3)在(2)的条件下,比较mx与kx+b的大小(直接写出结果).
解:当x<1时,kx+b>mx;当x=1时,kx+b=mx;当x>1时,kx+b<mx.
一次函数与方程、不等式
1.解一元一次方程:相当于在某个一次函数y=ax+b(a≠0)的函数值为0时,求自变量x的值.
2.解一元一次不等式:相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.
3.解二元一次方程组:从“数”的角度看相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少; 从“形”的角度看相当于确定两条直线的交点坐标.
请你根据图中图象所提供的信息解答下面问题:
(1)分别写出a1、a2中变量y随x变化而变化的情况;
a1:y随x的增大而增大;a2:y随x的增大而减小;
(2)求出一个二元一次方程组,使它满足图象中的两条直线的位置.
求满足图象中的两条直线的位置的一个二元一次方程组,即为求直线a1、a2的解析式.
人教版八年级下册19.2.2 一次函数习题课件ppt: 这是一份人教版八年级下册19.2.2 一次函数习题课件ppt,共22页。PPT课件主要包含了x>3,1求k的值等内容,欢迎下载使用。
数学八年级下册19.2.3一次函数与方程、不等式背景图ppt课件: 这是一份数学八年级下册19.2.3一次函数与方程、不等式背景图ppt课件,共24页。PPT课件主要包含了学习目标,小于-1,大于2,小于0,y3x+2,新知探究,从“数”的角度看,从“形”的角度看,取值范围,大于0等内容,欢迎下载使用。
人教版八年级下册19.2.3一次函数与方程、不等式课文配套ppt课件: 这是一份人教版八年级下册19.2.3一次函数与方程、不等式课文配套ppt课件,共9页。PPT课件主要包含了合并得2x4,化系数为1得x2,创设情境,y2x-4,y3x+2,y-1,B20,A06,∴图象位于x轴上方,∴图象位于x轴下方等内容,欢迎下载使用。












