












- 19.2.3《一次函数图象与性质》课件+教案+同步练习 课件 58 次下载
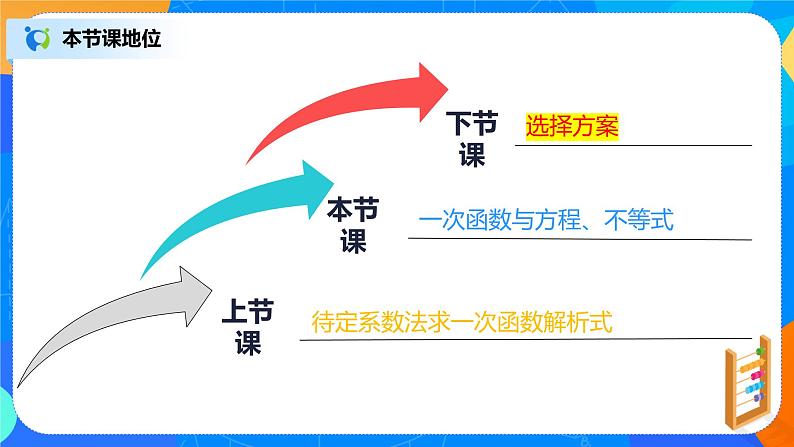
- 19.2.4《待定系数法求一次函数解析式》课件+教案+同步练习 课件 54 次下载
- 19.3《课题学习—选择方案》课件+教案+同步练习3 课件 44 次下载
- 19.4《章末复习》课件+教案+同步练习 课件 61 次下载
- 20.1.1《平均数概念》课件+教案+同步练习 课件 41 次下载
初中数学人教版八年级下册19.2.3一次函数与方程、不等式优质课课件ppt
展开待定系数法求一次函数解析式有理数
一次函数与方程、不等式
会从函数的角度看方程(组)的解(解集)的意义
会从函数的角度看不等式解集的意义
会将函数问题转化为解方程(组)或不等式(组)问题
会从函数的角度看方程或不等式的解的意义
(1)解方程5x+10=0。
(2)当自变量x为何值时,函数y=5x+10的值为0?
解:(1)5x+10=05x=-10x=-2
(2)当y=0时,即: 5x+10=05x=-10x=-2
前面我们学习了一次函数.实际上一次函数是两个变量之间符合一定关系的一种互相对应,互相依存。它与我们前面学过的一元一次方程、一元一次不等式、二元一次方程组有着必然的联系。从这节课开始,我们就学习用函数的观点去看待方程(组)与不等式,并充分利用函数图象的直观性,形象地看待方程(组)与不等式的求解问题。
1.解方程2x+20=0.
2.当x为何值时,函数y=2x+20的值为0?
当x=-10时,函数y=2x+20的值为0.
3.画出函数y=2x+20的图象,并确定它与x轴的交点坐标.
④问题① ②有何关系? ① ③呢?
从数上看, ① ②两个问题实际上是同一个问题.
① ③方程的解是直线与x轴交点的横坐标.
①解方程2x+20=0
②当x为何值时,函数y=2x+20的值为0?
③画出函数y=2x+20的图象,并确定它与x轴的交点坐标;
版块1、从函数的角度看一元一次方程
思考1:下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?(1)2x+1=3; (2)2x+1=0; (3)2x+1=-1.
方程2x+1=3的解是: ;即当 时,函数y=2x+1的值为3,也就是 ;
方程2x+1=-1的解是: ;即当 时,函数y=2x+1的值为-1,也就是 .
方程2x+1=0的解是: ;即当 时,函数y=2x+1的值为0,也就是 ;
思考1:下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看: 解一元一次方程 kx +b =c 就是求当函数(y=kx +b)值为c 时对应的自变量的值.
因为任何一个以x为求知数的一元一次方程都可以变形为y=ax+b(a≠0)的形式,所以解一元一次方程相当于在某个一次函数ax+b=0的函数值为 时,求 的值.
一次函数与一元一次方程的关系
求一元一次方程 kx+b=0的解.
一次函数y= kx+b中y=0时x的值.
求一元一次方程 kx+b=0的解.
求直线y= kx+b与 x 轴交点的横坐标.
例2、直线y=2x+b与x轴的交点坐标为(-5,0),则关于x的方程2x+b=0的解是x= .
例1 、直线y=-x+2与x轴交点坐标为(____,_____),这说明方程-x+2=0的解是x=_____.
版块2、从函数的角度看一元一次不等式
思考2:下面3个不等式有什么共同点和不同点?你能从函数的角度对解这3个不等式进行解释吗?(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
相同点:不等号左边都是 ,
不同点:不等号右边分别是 , , .
从函数的角度看,解这三个方程
不等式3x+2>2的解是: ;即当 _ 时,函数 ;
不等式3x+2<-1的解是______________;即当 时,函数 .
不等式3x+2<0的解是: ;即当 时,函数 ;
不等式kx+b>c的解集就是使函数y =kx+b 的函数值大于c的对应的自变量取值范围; 不等式kx+b<c的解集就是使函数y =kx+b 的函数值小于c的对应的自变量取值范围.
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.
求kx+b>0(或<0)(k≠0)的解集
y=kx+b的值大于(或小于)0时,x的取值范围
求kx+b>0(或<0)(k≠0)的解集
确定直线y=kx+b在x轴上方(或下方)的图象所对应的x取值范围
一次函数与一元一次不等式的关系
例3、画出函数y=-3x+6的图象,结合图象求:(1)不等式-3x+6>0 和-3x+6<0的解集;(2)当x取何值时,y<3?
解:(1)由图象可知,不等式-3x+6>0 的解集是x<2;不等式 -3x+6<0的解集x>2;
(2)由图象可知,当x>1时,y<3.
例4、如图,已知直线y=kx+b与x轴交于点(- 4,0),则当y>0时,x的取值范围是_________
1、直线y=ax+b在坐标系中的位置如图,则方程ax+b=0的解是χ=________
2、已知直线y=ax-b的图象如图所示,则关于x的方程ax-b=0的解为x= ,当x=0时,y= .
3、已知函数 y=x-5 , 当x____时,y>0;当 x____时,y<0。4、已知一次函数 y=kx+b的图象如图所示,则不等式 kx+b>0的解集是( )A.x>-2 B.x<-2C.x>-1 D.x<-1
5、已知直线 y=2x+k 与 x 轴的交点为 (-2,0),则关于x的不等式 2x+k<0 的解集是 ( )A. x>-2 B. x≥-2 C. x<-2 D. x≤-2
6、函数y=2x+6的图象如图,利用图象:
(1)求方程2x+6=0的解;
由图象可得:图象过点(-3,0).∴方程2x+6=0的解为x=-3;
(2)求不等式2x+6>0的解集;
由图象可得:当x>-3时,函数y=2x+6的图象在x轴上方.∴不等式2x+6>0的解集为x>-3;
(3)若-1≤y≤3,求x的取值范围.
由图象可得:函数图象过F(1.5,3),G(-3.5,-1)两点,当-3.5≤x≤-1.5时,函数y=2x+6的函数值满足-1≤y≤3,∴x的取值范围是-3.5≤x≤-1.5.
1.解一元一次方程:相当于在某个一次函数y=ax+b(a≠0)的函数值为0时,求自变量x的值.
2.解一元一次不等式:相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.
初中数学人教版八年级下册19.2.2 一次函数一等奖ppt课件: 这是一份初中数学人教版八年级下册19.2.2 一次函数一等奖ppt课件,共41页。PPT课件主要包含了谁对呢,情景引入,探究新知,解这3个方程,求自变量x的值,y2x+1,的横坐标分别为多少,看它们,yax+b,为9时自变量的值等内容,欢迎下载使用。
人教版八年级下册19.2.2 一次函数一等奖习题课件ppt: 这是一份人教版八年级下册19.2.2 一次函数一等奖习题课件ppt,文件包含1923《一次函数与方程不等式》课件pptx、192《习题》课件pptx、1923《一次函数与方程不等式》导学案doc、1923《一次函数与方程不等式》教案doc等4份课件配套教学资源,其中PPT共66页, 欢迎下载使用。
人教版八年级下册19.2.2 一次函数一等奖课件ppt: 这是一份人教版八年级下册19.2.2 一次函数一等奖课件ppt,文件包含1923一次函数与方程不等式pptx、1923一次函数与方程不等式导学案doc、1923一次函数与方程不等式教案doc等3份课件配套教学资源,其中PPT共42页, 欢迎下载使用。














