数学九年级下册29.1 投影课后复习题

这是一份数学九年级下册29.1 投影课后复习题，共5页。试卷主要包含了1 投影，CBCBB　6等内容，欢迎下载使用。
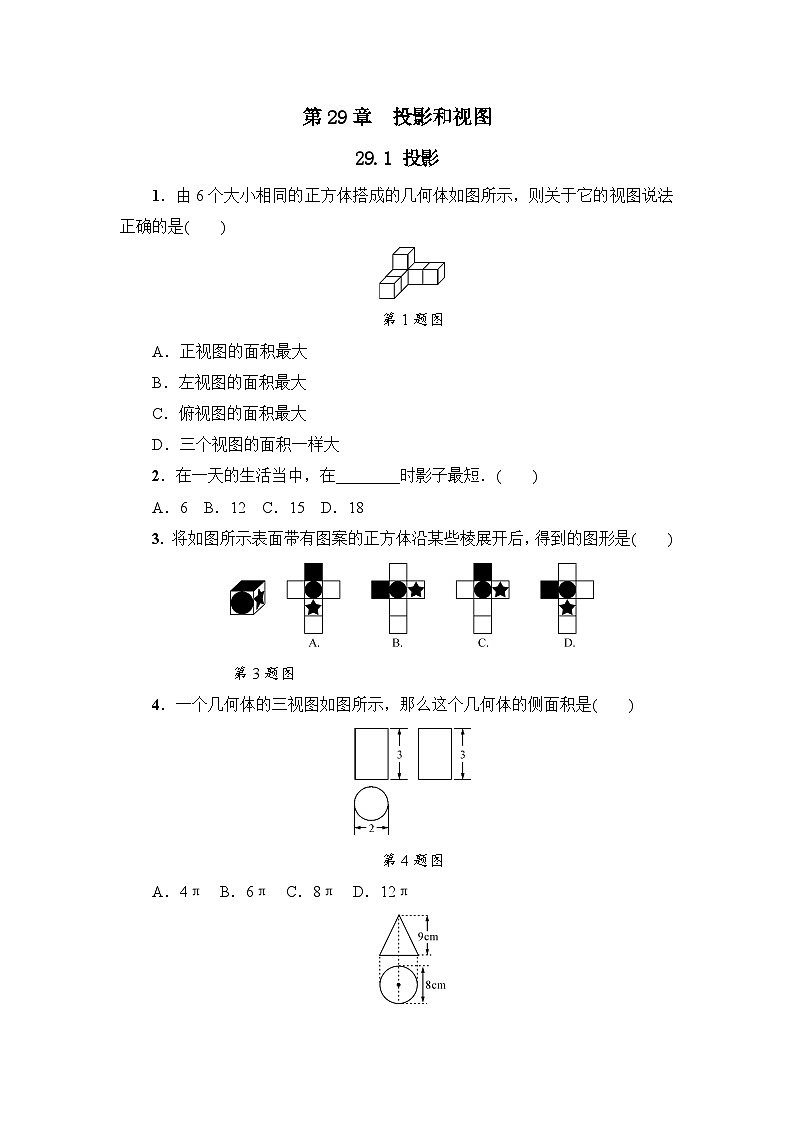
1．由6个大小相同的正方体搭成的几何体如图所示，则关于它的视图说法正确的是( )
第1题图
A．正视图的面积最大
B．左视图的面积最大
C．俯视图的面积最大
D．三个视图的面积一样大
2．在一天的生活当中，在________时影子最短．( )
A．6 B．12 C．15 D．18
3. 将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是( )
第3题图
4．一个几何体的三视图如图所示，那么这个几何体的侧面积是( )
第4题图
A．4π B．6π C．8π D．12π
第5题图
5．如图是一个立体图形的二视图，根据图示的数据求出这个立体图形的体积是( )
A．24πcm3
B．48πcm3
C．72πcm3
D．192πcm3
6．我们常说的三种视图是指_______________________ _______。
7．请写出三种视图都相同的两种几何体：___________________ _____。
8．小明的身高是1.6米，他的影长是2米，同一时刻古塔的影长是18米， 则古塔的高是________米．
9．某同学想利用影子长度测量操场上旗杆的高度，在某一时刻，他测得自己影子长为0.8m，立即去测量旗杆的影子长为5m，已知他的身高为1.6m，则旗杆的高度为________m.
10．如图为住宅区内的两幢楼，它们的高AB＝CD＝30m，两楼之间的距离AC＝24m，现需了解甲楼对乙楼的采光的影响情况，当太阳光与水平线的夹角为30°时，求甲楼的影子在乙楼上有多高？(精确到0.1m，eq \r(2)≈1.41，eq \r(3)≈1.73)
第10题图
11．如图，太阳光线与地面成60°角，一棵倾斜的大树在地面上所成的角为30°，这时测得大树在地面上的影长约为10m，试求此大树的长约是多少？(得数保留整数)
第11题图
12．如图，一电线杆AB的影子分别落在地上和墙上，某一时刻，小明竖起1m高的直杆，量得其影长为0.5m，此时，他又量得电线杆AB落在地上的影子BD长3m，落在墙上的影子CD的高为2m，小明用这些数据很快算出了电线杆AB的高，请你计算，电线杆AB的高为________．
第12题图
13．从卫生纸的包装纸上得到以下资料：两层300格，每格11.4cm×11cm，如图甲．用尺量出整卷卫生纸的半径(R)与纸筒内芯的半径(r)，分别为5.8cm和2.3cm，如图乙．那么该两层卫生纸的厚度约为多少cm？(π取3.14，结果精确到0.001cm)
第13题图
14．问题背景：在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：
甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm.
乙组：如图2，测得学校旗杆的影长为900cm.
丙组：如图3，测得校园景灯(灯罩视为球体，灯杆为圆柱体，其粗细忽略不计)的高度为200cm，影长为156cm.
第14题图
任务要求：
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度；
(2)如图3，设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息，求景灯灯罩的半径(友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562＋2082＝2602)．
答案
1—5.CBCBB 6. 主视图、俯视图、左视图 7. 球、正方体 8. 14.4 9. 10 10.
第10题图
设甲楼的影子在乙楼上的最高点为E，作EF⊥AB于F，在Rt△BFE中，∵∠BFE＝90°，∠BEF＝30°，∴BF＝eq \f(1,2)BE，根据勾股定理，得BF2＋EF2＝BE2，∴BF2＋242＝4BF2，即BF＝8eq \r(3)≈13.8m，∴CE＝AF＝AB－BF＝16.2(m)． 11. 过B作BM⊥AC于M，∵∠A＝30°，∠CBE＝60°，故∠ACB＝30°，∴BM＝eq \f(1,2)AB＝5，而BC＝AB＝10，∴AM＝5eq \r(3)，AC＝10eq \r(3)≈17m. 12. 8 m 13. 设两层卫生纸的厚度为xcm.11.4×11×x×300＝π(5.82－2.32)×11，37620x＝π(33.64－5.29)×11，x≈0.026. 答：两层卫生纸的厚度约为0.026cm. 14. (1)由题意可知：∠BAC＝∠EDF＝90°，∠BCA＝∠EFD.∴△ABC∽△DEF.∴eq \f(AB,DE)＝eq \f(AC,DF)，即eq \f(80,DE)＝eq \f(60,900).∴DE＝1200(cm)．所以，学校旗杆的高度是12m. (2)与(1)类似得：eq \f(AB,GN)＝eq \f(AC,GH)，即eq \f(80,GN)＝eq \f(60,156).∴GN＝208.在Rt△NGH中，根据勾股定理得：NH2＝1562＋2082＝2602.∴NH＝260.设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH.则∠OMN＝∠HGN＝90°，又∠ONM＝∠HNG.∴△OMN∽△HGN.∴eq \f(OM,HG)＝eq \f(ON,HN).又ON＝OK＋KN＝OK＋(GN－GK)＝r＋8.∴eq \f(r,156)＝eq \f(r＋8,260)，解得：r＝12.所以，景灯灯罩的半径是12cm.