初中人教版21.1 一元二次方程教学ppt课件

这是一份初中人教版21.1 一元二次方程教学ppt课件，共19页。PPT课件主要包含了条件∆≥0等内容，欢迎下载使用。

学习目标1）掌握一元二次方程根与系数的关系。2）利用一元二次方程根与系数的关系进行简单计算。重点掌握一元二次方程根与系数的关系。难点利用一元二次方程根与系数的关系进行简单计算。
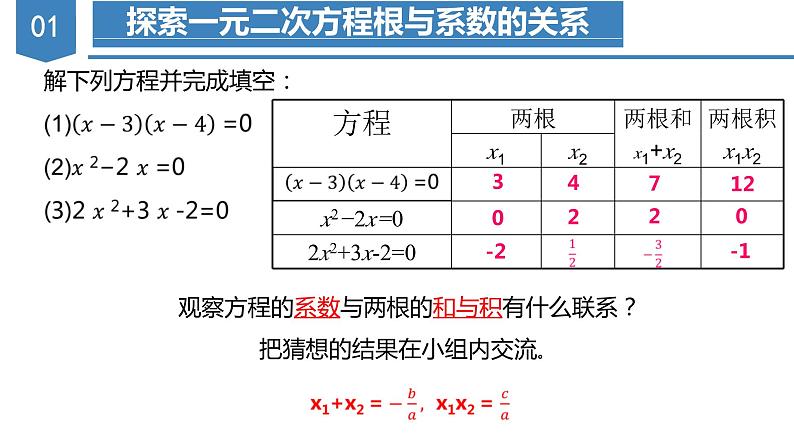
解下列方程并完成填空：
观察方程的系数与两根的和与积有什么联系？把猜想的结果在小组内交流。
根据两个多项式相等的规定，得
（考查一元二次方程根与系数的关系）
注意：1)必须先求证Δ ≥0才可以使用韦达定理 2)先把方程化为一般式，才能使用韦达定理
变式1-1 小明说：“一元二次方程x2+x+2=0中，两根之和为-1，两根之积为2。”你觉得他说的对吗？
不存在，一元二次方程x2+x+2=0中b2-4ac<0，方程无实数根。
（已知一元二次方程一个根求另一个根）
典例2 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1，则另一个解为（　　）A．1 B．﹣3C．3 D．4
【详解】设方程的另一个解为x1，根据题意得：﹣1+x1=2，解得：x1=3，故选C．
变式2-1 已知方程x2-(k+1)x+3k=0的一个根是2 ,求它的另一个根及k的值。
（利用根与系数的关系进行计算）
解：由根与系数的关系得x1+x2=-k,x1.x2=k+2，而x12+ x22 = 4 即(x1+ x2)2 -2x1x2=4 ∴k2- 2(k+2）=4 解得：k=4或k=－2 ∵ △= k2-4k-8 当k=4时， △＜0 当k=-2时，△＞0 ∴ k=-2
变式3-2 若一个矩形的长和宽是一元二次方程 x²-10x+20=0的两根，求这个矩形的周长和面积？
（利用根与系数的关系求解未知数的值）
（利用根与系数的关系进行计算）（提高）
变式5-1 若α，β是方程x2+2x﹣2005=0的两个实数根，则α2+3α+β的值为（　　）A．2005 B．2003C．﹣2005 D．4010
【详解】α,β是方程x2+2x−2005=0的两个实数根，则有α+β=−2.α是方程x2+2x−2005=0的根,得α2+2α−2005=0,即：α2+2α=2005.所以α2+3α+β=α2+2α+(α+β)=α2+2α−2=2005−2=2003，故选B.
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2，那么
根与系数的关系（韦达定理）