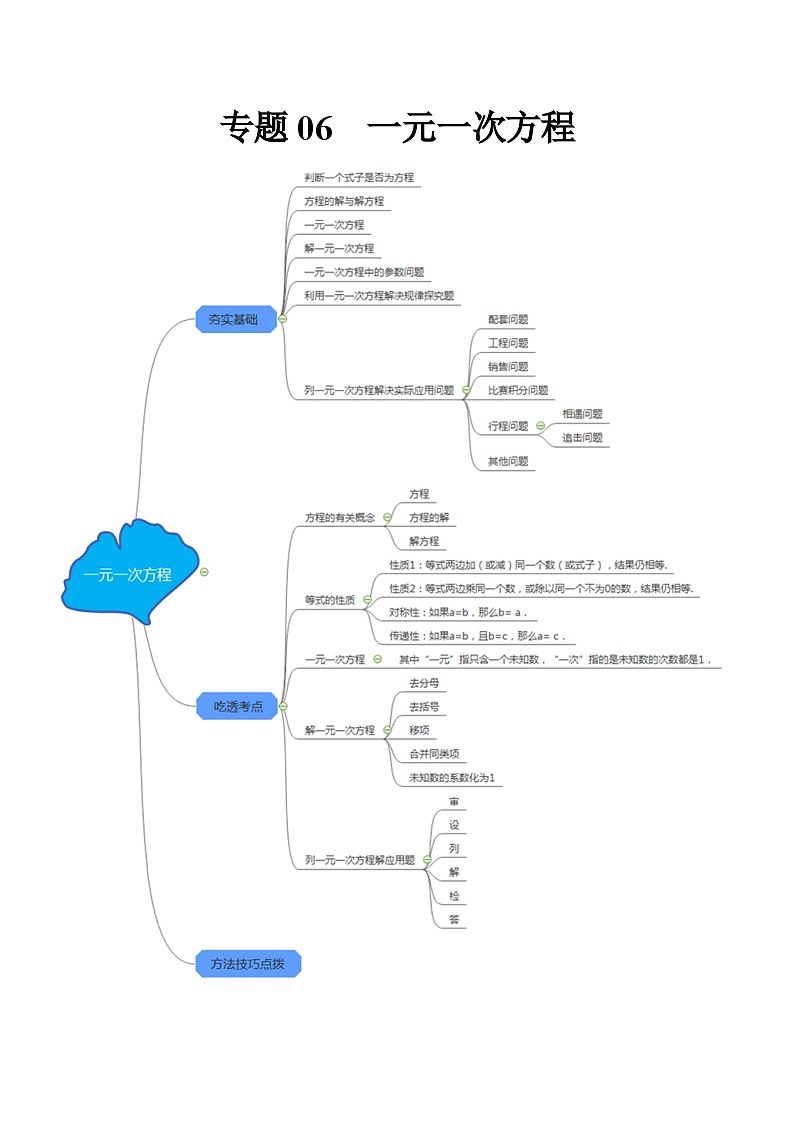
专题06 一元一次方程（夯实基础、考点分析）--2024年中考数学一轮复习（全国通用）

这是一份专题06 一元一次方程（夯实基础、考点分析）--2024年中考数学一轮复习（全国通用），共30页。试卷主要包含了方程的有关概念，等式的性质，一元一次方程，解一元一次方程的一般步骤，利用一元一次方程解决规律探究题，列一元一次方程解决实际应用问题等内容，欢迎下载使用。
夯实基础
1．方程的有关概念
（1）方程
含有未知数的等式叫做方程．
（2）方程的解
使方程中等号左右两边相等的未知数的值，叫做方程的解，只含有一个未知数的方程的解，也叫做方程的根．
（3）解方程
求方程解的过程，叫做解方程．
2．等式的性质
（1）等式的性质1：等式两边加（或减）同一个数（或式子），结果仍相等．
如果a=b，那么a±c= b±c．
（2）等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等．
如果a=b，那么ac= bc；如果a=b（c≠0），那么=．
（3）等式除了以上两条性质外，还有其他的一些性质：
①对称性：等式的左、右两边交换位置，所得的结果仍是等式．如果a=b，那么b= a．
②传递性：如果a=b，且b=c，那么a= c．等式的传递性，习惯上也称作是等量代换．
3．一元一次方程
只含有一个未知数，并且未知数的最高次数是1，这样的整式方程叫做一元一次方程．
（1）其中“一元”指只含一个未知数，“一次”指的是未知数的次数都是1．
（2）ax+b=0（a≠0）通常叫做关于x的一元一次方程的标准形式，其中，只有一个未知项ax，一个常数项b，方程右边是0．
4．解一元一次方程的一般步骤
去分母→去括号→移项→合并同类项→未知数的系数化为1
（1）去分母
①去分母的概念：一元一次方程中如果有分母，在方程的两边同时乘所有分母的最小公倍数，将分母去掉，这一变形过程叫做去分母．
②去分母的依据：等式的性质2，方程两边同时乘以各分母的最小公倍数．
③去分母的目的：使方程中不含分母，便于运算和变形 ．
④注意：在去分母的过程中，不能漏乘某些不含分母的项；分子是多项式时要加括号．
⑤若分母是小数（或分数），可先利用分数的基本性质，将分子、分母同时扩大若干倍，注意要加括号，此时，不是去分母，不能把方程其余的项也扩大若干倍．
（2）去括号
①去括号的概念：把方程中含有的括号去掉的过程叫做去括号．
②去括号的依据：分配律——．
③去括号的法则：将括号外的因数连同它前面的符号看成一个整体，按照分配律与括号内各项相乘．括号外的因数是正数，去括号后各项符号与原括号内相应的各项符号相同；括号外的因数是负数，去括号后各项符号与原括号内相应的各项符号相反．
④去括号的顺序：对于多重括号的，可以先去小括号，再去中括号，若有大括号，最后去大括号，或由外向内去括号，有时也可用去分母的方法去括号．
（3）移项
把等式一边的某项变号后移到另一边，叫做移项．
（4）合并同类项
把方程中含有的同类项合并，使方程变得简单，更接近于“x=a”的形式，合并时要牢记合并同类项的法则：同类项的系数相加，字母及字母的指数不变．
①合并同类项的实质是系数的合并，字母及其指数都不变．
②含不同未知数的项不能合并．
③系数是负数时，合并时注意不能丢了负号．
（5）未知数的系数化为1
将形如ax=b（a≠0）的方程化为x=的形式．
5．列一元一次方程解应用题的一般步骤
审：审题，分析题目中已知什么，求什么，明确各数量之间的关系；
设：用x来表示题目中的一个未知数，其他的未知数用含x的整式来表示；
列：寻找相等关系（有的由题目给出，有的由该问题所涉及的等量关系给出），列方程．根据题目中的等量关系列出方程；
解：解出所列出方程，求出未知数的值；
检：检验方程的解是否符合问题的实际意义；
答：写出答案．
▲列一元一次方程解应用题的关键是：寻找相等关系．
吃透考点
1．判断一个式子是否为方程：
（1）只需看两点：一是等式；二是含有未知数，二者缺一不可．
（2）不看未知数的个数，也不看未知数的次数．
（3）未知数可以是x，也可以是其他字母，如：y，s，t，v等．
（4）若题中有“××是关于**的方程”的条件，则字母**就是未知数，其他字母要当做已知数对待，这种方程也称为含字母参数的方程．
2．方程的解与解方程
（1）使方程左右两边相等的未知数的值可以不止一个，即方程的解可以有多个．
（2）方程的解和解方程是不同的概念，方程的解是求得的结果，解方程是求解的过程，要区别开．解方程的目的就是求出方程的解．
3．一元一次方程
（1）其中“一元”指只含一个未知数，“一次”指的是未知数的次数都是1．
（2）ax+b=0（a≠0）通常叫做关于x的一元一次方程的标准形式，其中，只有一个未知项ax，一个常数项b，方程右边是0．
4．解一元一次方程
（1）一般步骤：去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x=a形式转化．
（2）若方程中有的分母不是整数，可以先把分母化为整数，再根据等式的性质去分母；解一元一次方程的五个步骤不是一成不变的，要根据方程的特点和需要灵活选用；解完方程后，最好把求得的解分别代入原方程的左边和右边，看两边的值是否相等．
（3）在解类似于“ax+bx=c”的方程时，将方程左边，按合并同类项的方法并为一项即（a+b）x=c．使方程逐渐转化为ax=b的最简形式体现化归思想．
（4）解一元一次方程时先观察方程的形式和特点，若有分母一般先去分母；若既有分母又有括号，且括号外的项在乘括号内各项后能消去分母，就先去括号．将ax=b系数化为1时，要准确计算，一弄清求x时，方程两边除以的是a还是b，尤其a为分数时；二要准确判断符号，a、b同号x为正，a、b异号x为负．
5．一元一次方程中的参数问题
利用方程的解求方程中字母的值时，若两个方程中只有一个方程含有字母，则可以先求出不含字母的方程的解，再根据两个方程的解之间的关系求出另一个方程的解，进而求出字母的值；若两个方程都含有字母，则可以分别求出这两个方程的解（用字母参数表示），然后根据两个方程的解之间的关系列出新的方程，求解即可得到字母的值．
6．利用一元一次方程解决规律探究题
数字中的规律探究题一般是通过观察与猜想、类比与分析、探索与归纳题目所给的已知条件，发现题目中数字的规律．解决这类题的思路是找到相邻数字之间的关系，设数列中其中一个数为x，用x表示出相关各数，然后根据题中的相等关系列方程求解．有时设出的未知数不一定是数列中的数，也有可能是正整数n，要根据具体问题而定．
7．列一元一次方程解决实际应用问题
（1）配套问题
配套问题找准要配套物品之间的数量关系，根据它们的等量关系列出方程解答．
①配套问题常见的是“1：n”型，即1个甲种零件和n个乙种零件配成一个物件．但也有“n：m”型（n，m均不为1），后者在寻找相等关系、列方程时更容易出错．
②在解决配套问题时，为避免倍数乘错对象，可以先根据题目描述，将配套方式写成A：B=m：n的形式，然后利用外项之积=内项之积，化为An=Bm的形式．
（2）工程问题
工程问题的主要关系：工作总量=工作时间×工作效率．
①工程问题中的工作总量有两种情况：一种是具体的数量；另一种是看作总体“1”，此时工作效率=．
②几个人合作的工作效率等于各个人单独工作效率之和．
③工作总量=各部分工作量之和．
（3）销售问题
销售问题一般涉及打折、进价、原价、售价、利润、利润率等基本量及其关系．销售问题经常用到以下基本等量关系：
①利润=售价－进价．
②利润率=．
③售价=原价．
④售价=进价×（1＋利润率）．
（4）比赛积分问题
①有些比赛只有胜、负之分，如篮球比赛；有些比赛有胜、负、平之分，如足球比赛中的小组循环赛．
②涉及比赛的关键词：比赛场数、胜场数、平场数、负场数、胜场积分、平场积分、负场积分、总积分等．
③根据比赛积分规则，可得相等关系：某队的比赛总积分=该队的胜场积分（+该队的平场积分）+该队的负场积分．
④解决比赛积分问题时，首先要找出已知量和未知量以及题中涉及的等量关系，再根据等量关系列出方程．
⑤体育比赛中，每两个队之间进行一场比赛的赛制叫做单循环比赛．每两个队之间进行两场比赛的赛制叫做双循环比赛．
（5）行程问题
行程问题常用的相等关系：路程=速度×时间． 行程问题又分相遇问题、追及问题等．
①相遇问题
A．特点：相向而行
B．等量关系：双方所走路程之和=全部路程．
C．相遇问题中等量关系的寻找方法
▲从时间考虑：两人同时出发，相遇时两人所用时间相等．
▲从路程考虑：沿直线运动时，两人相向而行，相遇时两人所走路程之和等于全程；沿圆周运动时，两人由同一地点相背而行，第一次相遇时两人所走的路程之和为圆周长．
▲从速度考虑：两人相向而行，他们的相对速度等于他们的速度之和．
②追及问题中等量关系的寻找方法
▲从时间考虑：若同时出发，追及时两人所用的时间相等．
▲从路程考虑：沿直线运动时，两人所走路程之差等于需要赶上的距离；沿圆周运动时，两人所走路程之差等于一个圆周长（从同时、同向、同一地点出发）．
▲从速度考虑：两人的相对速度等于他们的速度之差．
考点1 方程的定义
【例1】（2023春•德城区校级月考）下列
①；
②；
③；
④；
⑤；
⑥，其中是方程的有
A．1个B．2个C．3个D．4个
【答案】
【解答】解：①、④是方程，共有2个，
故选：．
【变式练1】（2022秋•绵阳期末）下列所给条件，不能列出方程的是
A．某数比它的平方小6B．某数加上3，再乘以2等于14
C．某数与它的的差D．某数的3倍与7的和等于29
【答案】
【解答】解：设某数为，
、，是方程，故本选项错误；
、，是方程，故本选项错误；
、，不是方程，故本选项正确；
、，是方程，故本选项错误．
故选：．
【变式练2】（2023春•宛城区校级月考）在①；②；③④中方程有 个．
A．1B．2C．3D．4
【答案】
【解答】解：①，没有“”，不是方程；
②，没有未知数，不是方程；
③，是方程；
④，是方程．
故选：．
【变式练3】（2023春•太康县期中）在下列各式中：
①；
②；
③；
④；
⑤；
⑥；
⑦．
其中是方程的有 个．
A．3B．4C．5D．6
【答案】
【解答】解：①，是方程；
②，是方程；
③，是代数式，不是方程；
④，是不等式，不是方程；
⑤，是不等式，不是方程；
⑥，是等式，不是方程；
⑦，是方程；
所以是方程的有①②⑦共3个．
故选：．
【变式练4】（2023春•朝阳区期中）下列各式中，属于方程的是
A．B．C．D．
【答案】
【解答】解：、不含未知数，不是方程，不符合题意；
、不是等式，故不是方程，不符合题意；
、不是等式，故不是方程，不符合题意；
、是含有未知数的等式，是方程，符合题意．
故选：．
【变式练5】（2023春•南安市期中）下列各式中，不是方程的是
A．B．C．D．
【答案】
【解答】解：根据方程的定义可知，、、都是方程，不是方程，
故选：．
考点2 方程的解
【例2】（2023•东河区模拟）如果方程的解是，那么
A．B．C．D．
【解答】解：依题意，得
，
则，
所以．
故选：．
【变式练1】（2023春•蒸湘区期末）若是方程的解，则的值是
A．B．4C．D．8
【解答】解：
把代入方程
可得：，
解得：，
故选：．
【变式练2】（2022秋•长垣市期末）已知是关于的方程的一个解，则的值是
A．B．C．D．
【答案】
【解答】解：把代入方程得：，
解得：．
故选：．
【变式练3】（2022秋•裕华区期末）方程★，★处被盖住了一个数字，已知方程的解是，那么★处的数字是
A．1B．2C．3D．4
【解答】解：将代入方程，得：★，
解得：★，
即★处的数字是1，
故选：．
【变式练4】（2022秋•港南区期末）已知是方程的解，则的值是
A．2B．3C．7D．8
【答案】
【解答】解：把 代入方程，
得：，
解得：，
故选：．
【变式练5】（2022秋•玉林期末）若方程的解为，则的值为
A．10B．C．D．
【答案】
【解答】解：依题意，得
，即，
解得，．
故选：．
考点3 等式的性质
【例3】（2023•沙坪坝区校级开学）下列等式变形，错误的是
A．若，则B．若，则
C．若，则D．若，则
【答案】
【解答】解：．，
，故本选项不符合题意；
．，
，故本选项不符合题意；
．，
，故本选项不符合题意；
．当时，由不能推出，故本选项符合题意．
故选：．
【变式练1】（2023•衢江区三模）已知，下列等式不一定成立的是
A．B．C．D．
【答案】
【解答】解：，
，
故不符合题意，
，
，
故不符合题意；
，
，
故不符合题意；
，
当时不成立，故符合题意，
故选：．
【变式练2】（2023•泗县二模）若，，为互不相等的实数，且，则下列结论正确的是
A．B．C．D．
【答案】
【解答】解：，
，
．
故选：．
【变式练3】（2023•锡林浩特市三模）设、、是实数，正确的是
A．若，则B．若，则
C．若，则D．若，则
【答案】
【解答】解：．若，则，故该选项错误，不符合题意；
．若，则，故该选项正确，符合题意；
．若且，则，故该选项错误，不符合题意；
．若，则，故该选项错误，不符合题意；
故选：．
【变式练4】（2023•顺德区校级三模）下列等式变形中，不正确的是
A．若，则B．若，则
C．若，则D．若，则
【答案】
【解答】解：．，，故本选项不符合题意；
．，，，故本选项符合题意；
．，，故本选项不符合题意；
．，，故本选项不符合题意；
故选：．
【变式练5】（2023•岳麓区校级三模）下列变形中，正确的是
A．若，则B．若，则
C．若，则D．若，则
【答案】
【解答】解：．若，则，故错误，本选项不符合题意；
．若，则，故错误，本选项不符合题意；
．当时，若，则，故错误，本选项不符合题意；
．若，则，故正确，本选项符合题意．
故选：．
考点4 一元一次方程的定义
【例4】（2023•西乡塘区校级二模）下列方程中，是一元一次方程的是
A．B．C．D．
【答案】
【解答】解：．方程是二元一次方程，不是一元一次方程，故本选项不符合题意；
．方程是一元二次方程，不是一元一次方程，故本选项不符合题意；
．方程是一元一次方程，故本选项符合题意；
．方程是分式方程，不是一元一次方程，故本选项不符合题意；
故选：．
【变式练1】（2023•武威一模）若方程是关于的一元一次方程，则 ．
【答案】2023．
【解答】解：方程是关于的一元一次方程，
，
解得：，
．
故答案为：2023．
【变式练2】（2023•九江一模）已知是关于的一元一次方程，则值为 ．
【答案】．
【解答】解：根据一元一次方程的定义得到且，
由原方程，得解得，
，
，
解得．
故答案为：．
【变式练3】（2023•攀枝花模拟）已知方程．当 时，方程为一元一次方程；当 时，方程为二元一次方程．
【解答】解：由于方程未说明是否关于、的方程，所以要参考是否关于，或者关于的一元一次方程；
当且时，方程为关于的一元一次方程，解得；
当且时，方程为二元一次方程，解得．
故答案为：，1．
【变式练4】（2022•定远县模拟）方程是关于的一元一次方程，那么的值是
A．0B．7C．8D．10
【答案】
【解答】解：方程是关于的一元一次方程，
且，
解得：，
故选：．
【变式练5】（2021•饶平县校级模拟）已知方程是关于的一元一次方程，则的值是 ．
【答案】．
【解答】解：由一元一次方程的特点得，
解得：．
故答案为：．
考点5 一元一次方程的解
【例5】（2023•英德市二模）下列方程中，解是的方程是
A．B．C．D．
【答案】
【解答】解：．把代入方程得：左边，右边，左边右边，所以不是方程的解，故本选项不符合题意；
．把代入方程得：左边，右边，左边右边，所以不是方程的解，故本选项不符合题意；
．把代入方程得：左边，右边，左边右边，所以不是方程的解，故本选项不符合题意；
．把代入方程得：左边，右边，左边右边，所以是方程的解，故本选项不符合题意；
故选：．
【变式练1】（2023•新邵县校级一模）若关于的方程的解与方程的解互为相反数，则 ．
【解答】解：方程，
移项合并得：，
解得：，
把代入得：，
解得：，
故答案为：
【变式练2】（2023•长沙县二模）一元一次方程的解为，则 ．
【答案】1．
【解答】解：把代入方程得：，
解得：，
故答案为：1．
【变式练3】（2023•仁怀市模拟）若关于的方程的解为，则的值为 ．
【解答】解：关于的方程的解为，
，
解得：．
故答案为：．
【变式练4】（2023•漳平市一模）若是方程的解，则 ．
【解答】解：根据题意，得
，
解得，．
故答案为：．
【变式练5】（2022秋•临湘市期末）关于的方程的解是3，则的值为 ．
【解答】解：根据题意将代入得：，
解得：．
故填：4．
考点6 解一元一次方程
【例6】（2022秋•海门市期末）解方程时，去分母正确的是
A．B．
C．D．
【答案】
【解答】解：方程两边同时乘以6得：，
去括号得：．
故选：．
【变式练1】（2023•柯城区校级一模）解方程的第一步应是
A．去分母B．去括号C．移项D．合并
【解答】解：解方程的第一步应是去括号，
故选：．
【变式练2】（2023•青山区一模）若的值与互为相反数，则的值为
A．1B．C．3D．
【答案】
【解答】解：由题意，得，
解得；
故选：．
【变式练3】（2023•瓯海区二模）下列解方程过程正确的是
A．系数化为1，得
B．解得
C．移项得
D．去括号得
【答案】
【解答】解：、系数化为1，得，故本选项不合题意；
、解得，正确，故本选项符合题意；
、移项得，故本选项不合题意；
、去括号得，故本选项不合题意；
故选：．
【变式练4】（2023•海口模拟）代数式的值是5，请问是
A．B．6C．4D．5
【答案】
【解答】解：由题意得，．
．
故选：．
【变式练5】（2023•六安三模）关于的一元一次方程的解为 ．
【答案】．
【解答】解：去分母得：，
移项得：．
故答案为：．
考点7 含绝对值符号的一元一次方程
【例7】（2012•南京模拟）已知关于的方程的解满足，则的值是 10或 ．
【解答】解：
或
把或分别代入中
或．
【变式练1】（2012•增城区校级模拟）已知方程，那么方程的解是 ．
【解答】解：根据绝对值是2的数是．
则方程的解是：
故答案为：．
【变式练2】（2023春•宜阳县期中）方程的解为
A．B．C．或D．无解
【答案】
【解答】解：当，则，得．
．
当，则，得．
．
综上：或．
故选：．
【变式练3】（2022秋•开江县校级期末）解方程，则 或7 ．
【解答】解：根据绝对值的意义，将原方程可化为：（1）；（2）．
解（1）得，
解（2）得．
故填或7．
【变式练4】（2022秋•碑林区校级期末）若关于的方程有解，则的取值范围是 ．
【答案】．
【解答】解：方程有解，
方程，
即，
（1）当时，即或，
①时，方程有一个解；
②，此时方程无解．
所以当时，方程只有一个解；
（2）当时，即，，
①时，方程有两个不相等解，
②时，方程无解．
所以当时，方程有两个不相等解；
（3）当时，即或
①时，方程有一个解；
②，此时方程有两个不相等解．
所以当时，方程有三个解；
（4）当时，即，
①时，方程有两个不相等解，
②时，方程有两个不相等解．
所以当时，方程有四个不相等解．
故答案为：．
【变式练5】（2022春•遂宁期末）方程的解是
A．B．C．或D．或
【答案】
【解答】解：，
或．
当，则；
当，则．
综上：或1．
故选：．
考点8 同解方程
【例8】（2023•湛江二模）若方程和方程的解相同，则
A．1B．2C．D．
【答案】
【解答】解：解得，
将代入，
得，
解得．
故选：．
【变式练1】（2022•南山区模拟）若关于的方程与方程的解相同，则的值为
A．B．3C．D．4
【答案】
【解答】解：，
，
方程与方程的解相同，
方程的解，
，
，
故选：．
【变式练2】（2021•饶平县校级模拟）关于的方程与方程的解相同，则常数是
A．B．3C．2D．
【答案】
【解答】解：方程，
移项得：，
合并同类项得：，
解得：，
把代入得：
，
解得：．
故选：．
【变式练3】（2020•朝阳区校级模拟）关于的方程的解与的解相同，则的值为
A．B．2C．D．1
【解答】解：解方程，得
．
关于的方程的解与的解相同，
把代入，得
，
解得．
故选：．
【变式练4】（2019•历下区一模）若与的解相同，则的值为
A．8B．2C．D．6
【答案】
【解答】解：先解方程得：
；
把代入得：
，
．
故选：．
【变式练5】（2018•河北三模）关于的方程的解与方程的解相同，则的值是
A．0B．2C．D．
【解答】解：的解为，
方程的解与方程的解相同，
是方程的解，
，
故选：．
考点9 由实际问题抽象出一元一次方程
【例9】（2023•南漳县模拟）我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完．试问大、小和尚各多少人？设大和尚有人，依题意列方程得
A．B．
C．D．
【答案】
【解答】解：设大和尚有人，依题意列方程得，
，
故选：．
【变式练1】（2023•宁南县模拟）我国古代数学名著《张丘建算经》中记载：“今有清酒一斗直粟十斗，醑酒一斗直粟三斗，今持粟三斛，得酒五斗，问清，醑酒各几何？”大意是：现有一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清酒，醑酒各几斗？如果设清酒斗，那么可列方程为
A．B．
C．D．
【答案】
【解答】解：设清酒斗，则醑酒斗，
由题意可得：，
故选：．
【变式练2】（2023•新昌县模拟）《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安．今乙发已先二日，甲仍发长安．问几何日相逢？译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安．现乙先出发2日，甲才从长安出发．问多久后甲乙相逢？设乙出发日，甲乙相逢，则可列方程
A．B．C．D．
【答案】
【解答】解：设乙出发日，甲乙相逢，则甲出发日，故可列方程为：
．
故选：．
【变式练3】（2023•三明二模）《孙子算经》中有一道题，原文是：今有三人共车，二车空：二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车；若每2人共乘一车，最终剩余9个人无车可乘，问共有多少辆车？设共有辆车，则
A．B．C．D．
【答案】
【解答】解：由题意可得，
，
故选：．
【变式练4】（2023•郧西县模拟）《孙子算经》中有一道题，原文是：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车；若每2人共乘一车，则最终剩余9个人无车可乘，问共有多少人，多少辆车？设共有人，则可列方程为
A．B．C．D．
【答案】
【解答】解：依题意，得：．
故选：．
【变式练5】（2023•杭州二模）把一批图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺20本．设这个班有学生名，根据题意列方程正确的是
A．B．C．D．
【答案】
【解答】解：依题意得：．
故选：．
考点10 一元一次方程的应用
【例10】（2023•景县校级模拟）根据图中两人的对话，小南买平板电脑的预算是
A．3800元B．4800元C．5800元D．6800元
【答案】
【解答】解：设小南买平板电脑的预算是元，
则原售价为元，现售价为元，
根据题意知，，
解得：，
答：小南买平板电脑的预算是5800元．
故选：．
【变式练1】（2023•城区二模）欧拉是18世纪瑞士著名的数学大师，在他所著的《代数学入门》一书中，有这样一个问题：父亲死后，四个儿子按下述方式分了他的财产：老大拿了财产的一半少3000英镑，老二拿了财产的少1000英镑；老三拿了恰好是财产的；老四拿了财产的加上600英镑．问整个财产有多少？每个儿子分了多少？根据题意下列叙述正确的是
A．老大分了1000英镑B．老二分了2000英镑
C．老三分了3000英镑D．老四分了4000英镑
【答案】
【解答】解：设整个财产是英镑，则老大分了英镑，老二分了英镑，老三分了英镑，老四分了英镑，
根据题意得：，
解得：，
，，，，
老大、老二、老三、老四每人分了3000英镑．
故选：．
【变式练2】（2023•南皮县校级模拟）相传有个人不讲究说话艺术常引起误会，一天他设宴请客，他看到几个人没来，就自言自语：“怎么该来的还不来呢？”客人听了，心想难道我们是不该来的，于是已到的客人的一半走了，他一看十分着急，又说：“嗨，不该走的倒走了！”剩下的人一听，是我们该走啊！又有剩余客人的三分之一离开了，他着急地一拍大腿：“我说的不是他们．”于是剩下的6个人也走了，聪明的你知道最开始来了多少客人吗？
A．16B．18C．20D．22
【答案】
【解答】解：设开始来了位客人，根据题意得
解得：
答：开始来的客人一共是18位．
故选：．
【变式练3】（2023•淮阳区模拟）某商场按标价销售某品牌电器一件可获利1250元，利润率为．为了让利顾客，提高销量，今年“五一”期间，该商场按同一标价打九折销售该品牌电器．那么“五一”期间销售一件该品牌电器可获得的纯利润为
A．875元B．750元C．562.5元D．550元
【答案】
【解答】解：设某品牌电器的进价为元，则标价为元，
根据题意得：，
解得：，
，
“五一”期间销售一件该品牌电器可获得的纯利润为875元．
故选：．
【变式练4】（2023•河北模拟）某班级劳动时，将全班同学分成个小组，若每小组8人，则余下1人；若每小组9人，则有一组少5人．按下列哪个选项重新分组，能使每组人数相同？
A．6组B．7组C．8组D．9组
【答案】
【解答】解：由题意得：，
解得：，
则全班人数为：（人，
要使每组人数相同，则每小组7人，即可分成（组．
故选：．
【变式练5】（2023•岳阳三模）“曹冲称象”是流传很广的故事，如图，按照他的方法：先将象牵到大船上，并在船侧面标记水位，再将象牵出，然后往船上抬入20块等重的条形石，并在船上留3个搬运工，这时水位恰好到达标记位置，如果再抬入1块同样的条形石，船上只留1个搬运工，水位也恰好到达标记位置，已知搬运工体重均为120斤，则每块条形石的重量是
A．120斤B．240斤C．100斤D．160斤
【答案】
【解答】解：设每块条形石的重量是斤，
根据题意得：，
解得：，
每块条形石的重量是240斤．
故选：．
方
法
技
巧
点
拨
1．运用等式的性质变形时，等式两边要加都加，要减都减，或者两边同时都乘或除以，且加减乘或除以的为同一个数（或式子），注意除数不能为0．
2．将数学问题或实际问题中的等量关系，用一元一次方程表示出来，就是列一元一次方程．
实际问题列一元一次方程