高中数学湘教版（2019）必修 第二册5.1 随机事件与样本空间课文配套ppt课件

这是一份高中数学湘教版（2019）必修 第二册5.1 随机事件与样本空间课文配套ppt课件，共21页。PPT课件主要包含了新知初探·课前预习，题型探究·课堂解透，A⊆B，不可能，答案B，答案ABC，至少有一次中靶，易错警示，答案A等内容，欢迎下载使用。

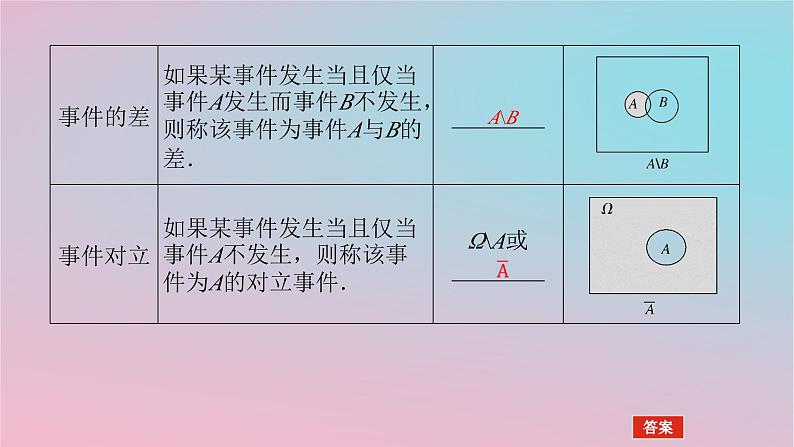
教材要点要点　事件的运算
状元随笔　(1)事件A与事件B互为对立事件，则集合A与集合B互为补集．(2)若事件A与事件B相互对立，那么事件A与事件B一定互斥，事件A与事件B互斥，A与B不一定对立．(3)事件A与事件B互为对立事件，也即事件A与事件B有且只有一个发生．
2．抽查10件产品，记事件A为“至少有2件次品”，则A的对立事件为(　　)A．至多有2件次品 B．至多有1件次品C．至多有2件正品 D．至少有2件正品
解析：至少有2件次品包含2，3，4，5，6，7，8，9，10件次品，共9种结果，故它的对立事件为含有1或0件次品，即至多有1件次品．
3．(多选)从一批产品中取出三件产品，设A＝“三件产品全不是次品”，B＝“三件产品全是次品”，C＝“三件产品有次品，但不全是次品”，则下列结论中正确的是(　　)A．A与C互斥 B．B与C互斥C．任何两个都互斥 D．任何两个都不互斥
解析：由题意知事件A、B、C两两不可能同时发生，因此两两互斥．
题型 1　事件关系的判断例1　某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，判断下列每对事件是不是互斥事件，如果是，再判断它们是不是对立事件：(1)“恰有1名男生”与“恰有2名男生”；(2)“至少有1名男生”与“全是男生”；(3)“至少有1名男生”与“全是女生”；(4)“至少有1名男生”与“至少有1名女生”．
解析：从3名男生和2名女生中任选2人有如下三种结果：2名男生，2名女生，1男1女．(1)“恰有1名男生”指1男1女，与“恰有2名男生”不能同时发生，它们是互斥事件；但是当选取的结果是2名女生时，该两事件都不发生，所以它们不是对立事件．(2)“至少有1名男生”包括2名男生和1男1女两种结果，与事件“全是男生”可能同时发生，所以它们不是互斥事件．(3)“至少有1名男生”与“全是女生”不可能同时发生，所以它们互斥，由于它们必有一个发生，所以它们是对立事件．(4)“至少有1名女生”包括1男1女与2名女生两种结果，当选出的是1男1女时，“至少有1名男生”与“至少有1名女生”同时发生，所以它们不是互斥事件．
方法归纳(1)要判断两个事件是不是互斥事件，只需要分别找出各个事件包含的所有结果，看它们之间能不能同时发生．在互斥的前提下，看两个事件的并事件是否为必然事件，从而可判断是否为对立事件．(2)事件的结果间是否有交事件，可考虑利用Venn图分析，对于较难判断的关系，也可考虑列出全部结果，再进行分析．
跟踪训练1　从40张扑克牌(红桃、黑桃、方块、梅花各10张，点数均为1～10)中任取一张．判断下面给出的每对事件是不是互斥事件，是不是对立事件，并说明理由．(1)“抽出红桃”与“抽出黑桃”；(2)“抽出红色牌”与“抽出黑色牌”；(3)“抽出的牌的点数为5的倍数”与“抽出的牌的点数大于9”． 
解析：(1)是互斥事件，但不是对立事件．理由：从40张扑克牌中任意抽取1张，“抽出红桃”和“抽出黑桃”是不可能同时发生的，所以是互斥事件．同时，不能保证其中必有一个发生，这是因为还可能抽出“方块”或者“梅花”，因此，二者不是对立事件．(2)既是互斥事件，又是对立事件．理由：从40张扑克牌中，任意抽取1张，“抽出红色牌”与“抽出黑色牌”，两个事件不可能同时发生，但其中必有一个发生，所以它们既是互斥事件，又是对立事件．(3)不是互斥事件，当然也不可能是对立事件．理由：从40张扑克牌中任意抽取1张，“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”这两个事件可能同时发生，如抽得点数为10的牌．因此，二者不是互斥事件，当然也不可能是对立事件．
题型 2　事件的运算例2　盒子里有6个红球、4个白球，现从中任取3个球，设事件A＝{取得的3个球有1个红球、2个白球}，事件B＝{取得的3个球有2个红球、1个白球}，事件C＝{取得的3个球至少有1个红球}，事件D＝{取得的3个球既有红球又有白球}．问：(1)事件D与A，B是什么样的运算关系？(2)事件C与A的交事件是什么事件？
变式探究　在本例中，设事件E＝{3个红球}，事件F＝{3个球中至少有一个白球}，那么事件C与B，E是什么运算关系？C与F的交事件是什么？
方法归纳事件间的运算方法(1)利用事件间运算的定义．列出同一条件下的试验所有可能出现的结果，分析并利用这些结果进行事件间的运算．(2)利用Venn图．借助集合间运算的思想，分析同一条件下的试验所有可能出现的结果，把这些结果在图中列出，进行运算．
题型 3　多个事件运算的表示例3　设有A，B，C三个事件，用A，B，C的运算表示以下事件：(1)A，B，C至少有一个发生；(2)A，B，C同时发生；(3)A，B，C都不发生；(4)仅A发生；(5)A，B，C仅有一个发生．
跟踪训练3　甲、乙、丙三人各投一次篮，分别记事件A＝“甲投中”，B＝“乙投中”，C＝“丙投中”，试用A，B，C表示下列事件：(1)甲、乙投中但丙没投中；(2)甲、乙、丙都投中；(3)甲、乙、丙三人至少有一人投中；(4)只有乙投中．
“三件产品不全是次品”或“三件产品中至少有一件正品”
解析：从一批产品中取出三件产品，试验的结果有四种：“三件正品”“二件正品一件次品”“一件正品二件次品”“三件次品”，故“三件产品全是次品”的对立事件是“三件产品不全是次品”．
课堂十分钟1．一个人打靶时连续射击两次，事件“至多有一次中靶”的互斥事件是(　　)A．两次都中靶 B．至少有一次中靶C．两次都不中靶 D．只有一次中靶
解析：事件“至多有一次中靶”包含“只有一次中靶”和“两次都不中靶”，因此不会与其同时发生的事件是“两次都中靶”．
2．掷一枚骰子，观察结果，A＝{向上的点数为3}，B＝{向上的点数为奇数}，则(　　)A．A⊆B B．A⊇BC．A＝B D．A，B互斥
解析：B＝{向上的点数为奇数}，即{向上的点数为1，3或5}，所以A⊆B.