压轴题型01 函数的性质-2024年高考数学二轮冲刺之压轴题专项训练（新高考专用）

这是一份压轴题型01 函数的性质-2024年高考数学二轮冲刺之压轴题专项训练（新高考专用），共36页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。


综合近几年高考对于函数性质的考察形式，2024年高考对于函数性质的考察仍然是重点。高考函数的性质常以基础题或中档题以上的题型出现，尤其对函数的零点的考察近几年常以压轴题型出现.
EQ \\ac(○,热) EQ \\ac(○,点) EQ \\ac(○,题) EQ \\ac(○,型)1 函数满足对定义域内任一实数（其中为常数）,
①，则是以为周期的周期函数；
②，则是以为周期的周期函数；
③，则是以为周期的周期函数；
④，则是以为周期的周期函数；
⑤，则是以为周期的周期函数.
⑥，则是以为周期的周期函数.
⑦，则是以为周期的周期函数.
⑧函数满足（），若为奇函数，则其周期为，若为偶函数，则其周期为.
EQ \\ac(○,热) EQ \\ac(○,点) EQ \\ac(○,题) EQ \\ac(○,型)2 常见几个奇函数：
一、单选题
1．函数是定义在R上奇函数，且，，则（ ）
A．0B．C．2D．1
【答案】B
【分析】通过已知计算得出函数是周期为8的周期函数，则，根据已知得出，即可得出答案.
【详解】函数是定义在R上奇函数，且，
，
，
则函数是周期为8的周期函数，
则，
令，则，
，
故选：B.
2．设偶函数f(x)＝lga|x＋b|在(0，＋∞)上单调递减，则f(b－2)与f(a＋1)的大小关系为
A．f(b－2)＝f(a＋1)B．f(b－2)>f(a＋1)
C．f(b－2)【答案】C
【详解】∵函数f(x)是偶函数，∴b＝0，此时f(x)＝lga|x|.
当a>1时，函数f(x)＝lga|x|在(0，＋∞)上是增函数，不合题意；
当0f(2)＝f(-2)=f(b－2)．
综上，可知f(b－2)3．函数的图象可能是下图中的（ ）
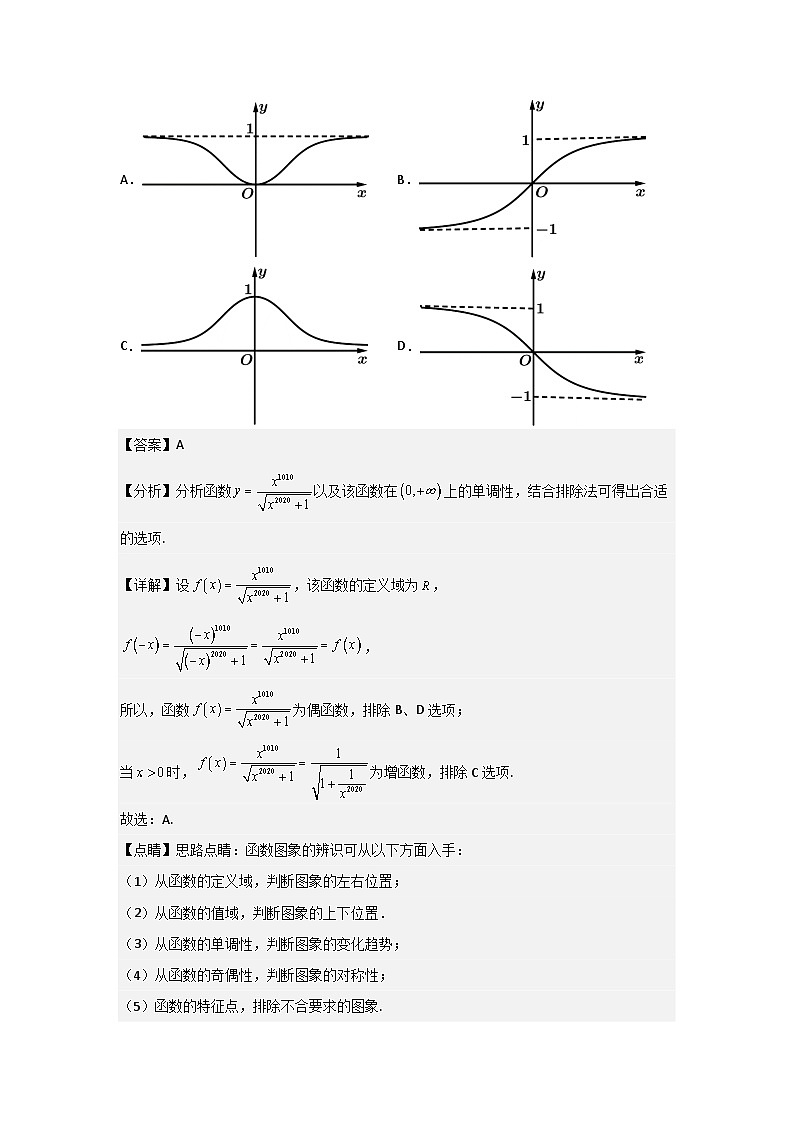
A．B．
C．D．
【答案】A
【分析】分析函数以及该函数在上的单调性，结合排除法可得出合适的选项.
【详解】设，该函数的定义域为，，
所以，函数为偶函数，排除B、D选项；
当时，为增函数，排除C选项.
故选：A.
【点睛】思路点睛：函数图象的辨识可从以下方面入手：
（1）从函数的定义域，判断图象的左右位置；
（2）从函数的值域，判断图象的上下位置．
（3）从函数的单调性，判断图象的变化趋势；
（4）从函数的奇偶性，判断图象的对称性；
（5）函数的特征点，排除不合要求的图象.
4．已知函数对任意，都有成立，又函数的图象关于点对称，且，则（ ）
A．－3B．－1C．1D．3
【答案】A
【分析】根据题意判断函数的对称性以及奇偶性，继而可推得函数的周期，根据函数的周期即可求得答案.
【详解】因为对任意，都有,所以函数的图象关于直线对称，
即，则，
又函数的图象关于点对称，则函数的图象关于点对称，
即函数为奇函数，
所以，所以，
所以8是函数的一个周期，
故，
故选：A．
5．函数在单调递减，且为奇函数，若，则满足的的取值范围为（ ）
A．B．C．D．
【答案】B
【解析】根据函数的奇偶性以及函数的单调性求出的范围即可．
【详解】解：因为为奇函数，
所以，
于是等价于，
又在单调递减，
，
．
故选：B．
【点睛】本题考查了函数的单调性和奇偶性问题，考查转化思想，属于中档题．
6．对于方程为的曲线给出以下三个命题:
（1）曲线关于原点对称；（2）曲线关于轴对称，也关于轴对称，且轴和轴是曲线仅有的两条对称轴；（3）若分别在第一、第二、第三、第四象限的点，都在曲线上，则四边形每一条边的边长都大于2；
其中正确的命题是（ ）
A．（1）（2）B．（1）（3）C．（2）（3）D．（1）（2）（3）
【答案】B
【分析】分段去绝对值，作出图象即可判定.
【详解】当时，，即；
当时，，即；
当时，，即；
当时，，即，
作图，如图所示：
所以曲线关于原点对称，（1）正确；
曲线的对称轴为轴和轴和和，（2）错误；
分别在第一、第二、第三、第四象限的点都在曲线上，任意边长都大于渐近线之间的距离，即四边形每一条边的边长都大于2，所以（3）正确.
故选：B
【点睛】此题考查根据方程分析曲线的特征，涉及分类讨论思想和对称性的讨论，对数形结合思想要求比较高..
二、多选题
7．已知定义域为的函数在上单调递增，，且图象关于对称，则（ ）
A．周期B．在单调递减
C．满足D．在上可能有1012个零点
【答案】ABD
【分析】对A选项首先得到其对称轴为，再根据关于对称，最终得到，则其周期为4，对B选项，根据函数周期性，单调性以及对称性即可得到其在单调递减，对C选项，根据周期性有，，，再结合其对称性即可判断，对D选项，得到函数在上有两零点，则在上可能有1012个零点.
【详解】A选项：由知的对称轴为，且，又图象关于对称，即，故，所以，即，所以，的周期为4，正确；
B选项：因为在上单调递增，，所以在上单调递增，又图象关于对称，所以在上单调递增，因为关于对称，所以在上单调递减，，故在单调递减，B正确；
C选项：根据周期性，，，，因为关于对称，所以，，故，错误；D选项：在上，，有2个零点，所以在上有1010个零点，在上有2个零点，故在上可能有1012个零点，正确，
故选：ABD．
【点睛】方法点睛：①如果，则关于直线对称；
②如果或，则关于点对称；
③如果，则关于.
8．已知函数，均为定义在上的奇函数，且，，则（ ）
A．是奇函数B．是奇函数
C．是偶函数D．是偶函数
【答案】ABC
【分析】根据题意，函数，均为定义在上的奇函数，利用奇偶函数的定义，可以依次判断ABC正确，可以证明D是奇函数，故D错误.
【详解】因为函数，均为定义在上的奇函数，所以，，
对于A选项，设，则，所以为奇函数，故A正确；
对于B选项，设，则，所以为奇函数，故B正确；
对于C选项，设，则，
所以为偶函数，故C正确；
对于D选项，设，则，所以是奇函数，故D错误.
故选：ABC.
9．已知定义在上的函数，对于任意的恒有，且，若存在正数，使得.给出下列四个结论:
①；②；③为偶函数；④为周期函数.
其中正确的结论的编号是
A．①B．②C．③D．④
【答案】ACD
【解析】取即可得到①正确；取可知②错误；取，可得，知③正确；取，可化简得到，可知为周期，④正确.
【详解】取，则
，①正确；
取，则 ，②错误；
取，则
为偶函数，③正确；
取，，则

为周期函数，④正确.
故选：
【点睛】本题考查抽象函数的性质的求解问题，解决此类问题常采用赋值法的方式配凑出所需的形式，进而得到函数性质.
三、填空题
10．函数的值域为___________.
【答案】.
【分析】利用分离常数法，将变形为，判断其单调性后，求其值域即可.
【详解】（），
是由函数向右平移1个单位，向下平移2个单位得到，
即在区间上为单调递增，在区间上为单调递增，
则函数的值域为.
故答案为：.
11．已知函数的图象关于原点中心对称，则实数______．
【答案】－1
【分析】利用算出答案即可.
【详解】因为函数的图象关于原点中心对称，
所以，即
所以，所以
故答案为：
12．若函数为奇函数，则______．
【答案】1
【分析】由函数在时有意义，且为奇函数，由奇函数的性质可得，求出再代入求解即可.
【详解】解：因为函数为奇函数，
所以，即，
所以，
所以，
故答案为.
【点睛】本题考查了函数的奇偶性，重点考查了奇函数的性质，属基础题.
13．已知，且在恒成立，则的值为__________.
【答案】
【分析】等价于，在恒成立，只需，根据的对称轴分类讨论，求出在的最大值和最小值，结合不等式的性质，即可求解.
【详解】，对称轴方程为，
在恒成立，需，
当时， ，
①②得，不合题意舍去；
当时， ，
③④得，不合题意舍去；
当

⑤⑥⑦得，
，代入⑤⑦得，
.
故答案为:.
【点睛】本题考查二次函数的最值以及不等式的性质，考查分类讨论思想，属于较难题.
四、解答题
14．已知函数.
(1)根据定义证明：函数在区间上单调递减；
(2)若实数a满足，求实数a的取值范围.
【答案】(1)证明见解析
(2)
【分析】（1）根据单调性的定义分析证明；
（2）根据题意先分和两种情况讨论，分析运算，对于方程，构建，结合单调性分析其零点，运算求解.
【详解】（1）
，且，
则，
∵，则，
∴，即，
故函数在区间上单调递减．
（2）当时，则成立，
则或，解得或；
当时，则，即，
设函数，
对，且，
∵函数在区间上单调递减，且在区间上单调递增，
则，即，
∴，即，
故函数在区间上单调递减，且，
即方程有且仅有一个根，
故，可得，
则或，解得，
综上所述：实数a的取值范围为．
【点睛】关键点点睛：
（1）对于，以为整体，分和两种情况分析运算；
（2）对于方程，直接求解不行时，通过构建函数，将方程的根的问题转化为函数的零点问题，结合单调性求其零点.
15．已知二次函数满足，且．
(1)求的解析式；
(2)已知，讨论在上的最小值；
(3)若当时，不等式恒成立，求实数a的取值范围．
【答案】(1)
(2)答案见解析
(3)
【分析】（1）设，代入得到值，计算，得到方程组，解出值，即可得到解析式；
（2）分，和讨论，结合函数单调性即可得到其最小值；
（3）不等式化简为，分和讨论，当时，利用函数的单调性即可得到不等式组，解出即可.
【详解】（1）设，因为，所以，
则
因为，
所以解得
故．
（2）．
当，即时，在上单调递减，
所以；
当且，即时，
在上单调递减，在上单调递增，
所以；
当时，在上单调递增，
所以．
综上，当时，；
当时，；
当时，．
（3）不等式可化简为．
因为，所以．
要使时，恒成立，显然时不可能．
当时，因为函数、在上均为增函数，
则函数在单调递增，故解得．
综上可知，实数的取值范围为．
【点睛】关键点睛：本题第二问属于轴定区间动问题，对其分类讨论的情况需要结合其开口方向，所问的是最大值还是最小值，抓住对称轴这一关键位置，数形结合讨论最值，第三问是一个函数恒成立问题，本问需要对进行分类讨论，尤其是当时，需要构造新函数，利用其单调性得到不等式组.
16．已知定义在的函数满足以下条件：
①；
②当时，；
③对，均有．
(1)求和的值；
(2)判断并证明的单调性；
(3)求不等式的解集．
【答案】(1)，；
(2)在上单调递增，证明见解析；
(3).
【分析】（1）利用赋值法求解即可；
（2）利用单调性的定义结合已知条件证明即可；
（3）由（2）可知当时，，则，所以将原不等式转化为，再由已知条件可得，由于，则，再转化为，再构造函数，再由其单调性和可求得结果.
【详解】（1）因为，，
所以令，则，
令，则，
令，则，即，
得或，
令，则，即，
若，则，与已知矛盾，
所以；
（2）在上单调递增，证明如下：
任取，且，则
，
所以，
则
，
令，则，
所以，
当时，，所以，
所以，则，
所以，即，
所以当时，，
所以，
因为，
所以，即，
所以在上单调递增；
（3）由（2）可知当时，，
所以，
所以可化为，
所以，
所以，
所以，
因为在上单调递增，
所以，
令，则在上单调递增，
因为，
所以可化为，
所以，
即原不等式的解集为.
【点睛】关键点点睛：此题考查函数的综合应用，考查函数单调性的证明和应用，考查利用函数的单调性证明不等式，第（3）问解题的关键是将原不等式转化为，再次转化为，再由的单调性转化为，然后构造函数利用其单调性可求得不等式的解集，考查数学转化思想，属于较难题.
17．已知是上的奇函数，且当时，，求的解析式．
【答案】
【分析】利用函数的奇偶性求得正确答案.
【详解】是定义在上的奇函数，
所以，
当时，，，
所以.
18．已知，，在下列条件下，求实数a的取值范围．
(1)对于，成立；
(2)对于，，成立．
【答案】(1)
(2)
【分析】（1）由题意，得利用基本不等式求出，即可得a的范围
（2）由题意，得，继而得，从而求出a的范围．
（1）
因为当时， 恒成立，
所以，
而当且仅当时，取等号
故，
故，即a的取值范围是；
（2）
因为对于，，成立
故当，时，，
因为在递减，递增，且，，
故，
而在递减，
故
所以，解得，即a的取值范围是．
19．已知函数.
（1）判断函数的奇偶性并证明；
（2）若不等式在上恒成立，求实数k的取值范围；
（3）当时，函数的值域为，求实数t的取值范围.
【答案】（1）偶函数，证明见解析；（2）；（3）．
【分析】（1）根据奇偶性定义证明；
（2）不等式用分离参数法变形后转化为求二次函数的最值可得参数范围；
（3）利用单调性求出的值域，从而得的值域，比较可得关于的方程有两个不等的正实根，由二次方程根的分布可得参数范围．
【详解】（1）是偶函数．证明如下：
函数定义域是，
，所以是偶函数；
（2）不等式为，即，此不等式在上恒成立，
由于，对称轴为，因此时，，所以，
所以 ，即取值范围是；
（3），时，是增函数，
所以时，，
而，所以，的值域是，
由题意，
所以有两个不等的正实根，
方程整理为：，
，解得．
所以的取值范围是．
20．已知函数f（x）＝x2﹣2x+1+a在区间[1，2]上有最小值﹣1．
（1）求实数a的值；
（2）若关于x的方程f（lg2x）+1﹣2klg2x＝0在[2，4]上有解，求实数k的取值范围；
（3）若对任意的x1，x2∈（1，2]，任意的p∈[﹣1，1]，都有|f（x1）﹣f（x2）|≤m2﹣2mp﹣2成立，求实数m的取值范围．（附：函数g（t）＝t在（0，1）单调递减，在（1，+∞）单调递增．）
【答案】（1）﹣1；（2）0≤t ；（3）m≤﹣3或m≥3．
【分析】（1）由二次函数的图像与性质即可求解.
（2）采用换元把方程化为t2﹣（2+2k）t+1＝0在[1，2]上有解，然后再分离参数法，化为
t与2+2k在[1，2]上有交点即可求解.
（3）求出|f（x1）﹣f（x2）|max＜1，把问题转化为1≤m2﹣2mp﹣2恒成立，研究关于
的函数h（p）＝﹣2mp+m2﹣3，使其最小值大于零即可.
【详解】（1）函数f（x）＝x2﹣2x+1+a对称轴为x＝1，
所以在区间[1，2]上f（x）min＝f（1）＝a，
由根据题意函数f（x）＝x2﹣2x+1+a在区间[1，2]上有最小值﹣1．
所以a＝﹣1．
（2）由（1）知f（x）＝x2﹣2x，
若关于x的方程f（lg2x）+1﹣2k•lg2x＝0在[2，4]上有解，
令t＝lg2x，t∈[1，2]
则f（t）+1﹣2kt＝0，即t2﹣（2+2k）t+1＝0在[1，2]上有解，
t2+2k在[1，2]上有解，
令函数g（t）＝t，
在（0，1）单调递减，在（1，+∞）单调递增．
所以g（1）≤2+2k≤g（2），
即2≤2+2t，
解得0≤t．
（3）若对任意的x1，x2∈（1，2]，|f（x1）﹣f（x2）|max＜1，
若对任意的x1，x2∈（1，2]，任意的p∈[﹣1，1]，
都有|f（x1）﹣f（x2）|≤m2﹣2mp﹣2成立，
则1≤m2﹣2mp﹣2，即m2﹣2mp﹣3≥0，
令h（p）＝﹣2mp+m2﹣3，
所以h（﹣1）＝2m+m2﹣3≥0，且h（1）＝﹣2m+m2﹣3≥0，
解得m≤﹣3或m≥3．