初中数学人教版九年级下册26.2 实际问题与反比例函数课时作业

这是一份初中数学人教版九年级下册26.2 实际问题与反比例函数课时作业，共7页。试卷主要包含了单选题，四象限,且y随x的增大而增大，解答题等内容，欢迎下载使用。


一、单选题
1．如图：在平面直角坐标系中，直线AB与轴交于点A（－2，0），与轴夹角为30°，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线上，则的值（ ）
A．－4B．－2C．D．
2．一款简易电子秤的工作原理：一个装有踏板（踏板质量忽略不计）的可变电阻，与踏板人的质量m之间的函数关系式为，其图象如图1所示；图2的电路中，电源电压恒为12伏，定值电阻的阻值为60欧，接通开关，人站上踏板，电流表显示的读数为I安，该读数可以换算为人的质量m，电流表量程为0~0.2安（温馨提示：导体两端的电压U，导体的电阻R，通过导体的电流I，满足关系式），则下面结论错误的为（ ）
A．用含I的代数式表示为
B．电子体重秤可称的最大质量为120千克
C．当时，若电源电压U为12（伏），则定值电阻最小为70（欧）
D．当时，若定值电阻为40（欧），则电源电压U最大为10（伏）
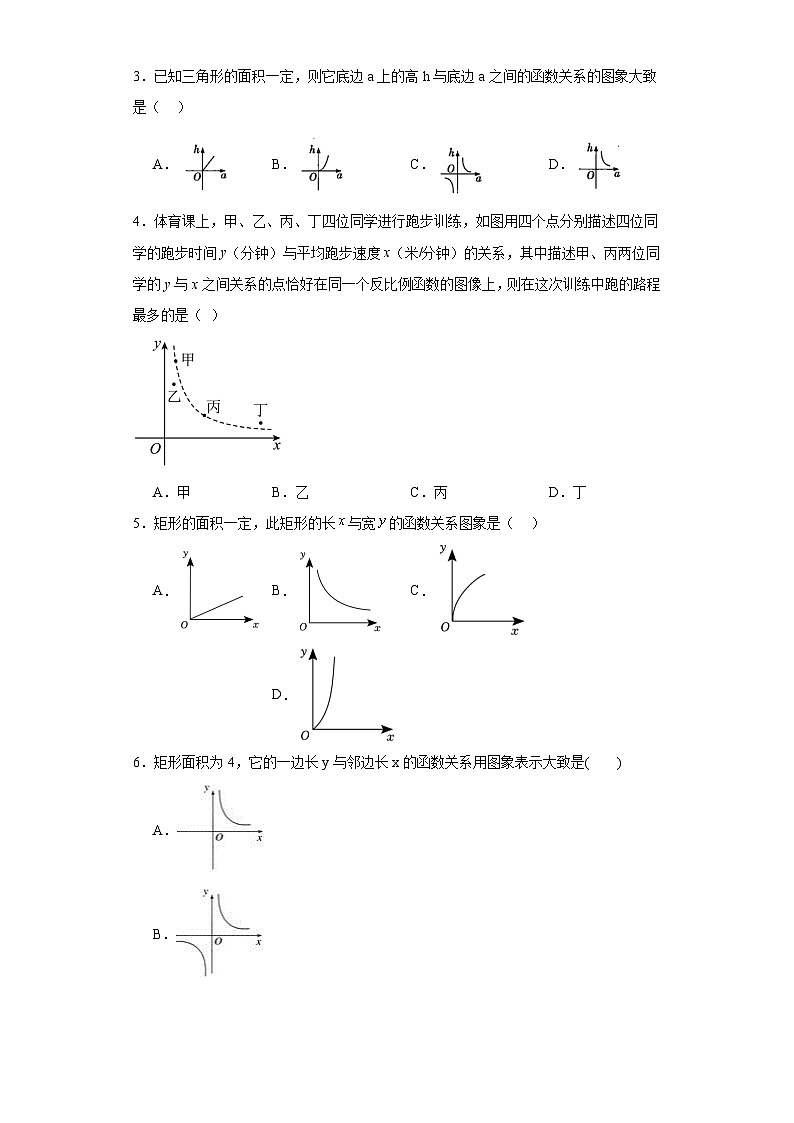
3．已知三角形的面积一定，则它底边a上的高h与底边a之间的函数关系的图象大致是（ ）
A．B．C．D．
4．体育课上，甲、乙、丙、丁四位同学进行跑步训练，如图用四个点分别描述四位同学的跑步时间y（分钟）与平均跑步速度x（米/分钟）的关系，其中描述甲、丙两位同学的y与x之间关系的点恰好在同一个反比例函数的图像上，则在这次训练中跑的路程最多的是（ ）

A．甲B．乙C．丙D．丁
5．矩形的面积一定，此矩形的长与宽的函数关系图象是（ ）
A．B．C．D．
6．矩形面积为4，它的一边长y与邻边长x的函数关系用图象表示大致是( )
A．
B．
C．
D．
7．若点A（2，3）、B（a﹣1，﹣2）都在函数y=的图象上，则a的值是（ ）
A．3B．2C．﹣3D．﹣2
8．如图，平面直角坐标系中，，反比例函数的图象分别与线段交于点，连接．若点关于的对称点恰好在上，则（ ）
A．B．C．D．
9．已知一个矩形的面积为24 cm2,其长为y cm,宽为x cm,则y与x之间的函数关系的图象大致在
A．第一、三象限,且y随x的增大而减小
B．第一象限,且y随x的增大而减小
C．第二、四象限,且y随x的增大而增大
D．第二象限,且y随x的增大而增大
10．一项工作，一个人单独完成需12天，若m个人共同完成需n天，选取6组数对，在坐标系中进行描点，则正确的是（ ）
A． B．
C． D．
二、填空题
11．每年春季为预防流感，某校利用休息日对教室进行药熏消毒，已知药物燃烧过程及燃烧完后空气中的含药量y（mg/m3）与时间x（h）之间的关系如图所示，根据消毒要求，空气中的含药量不低于3mg/m3且持续时间不能低于10h．请你帮助计算一下，当空气中的含药量不低于3mg/m3时，持续时间可以达到 h．
12．如图，若点M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别交函数y=（x＜0）和y=（x＞0）的图象于点P和Q，连接OP和OQ．以下列结论：
①∠POQ不可能等于90°；
②；
③这两个函数的图象一定关于y轴对称；
④若S△POM=S△QOM，则k1+k2=0；
⑤△POQ的面积是（|k1|+|k2|）．
其中正确的有 （填写序号）．
13．有x个小朋友平均分20个苹果，每人分得的苹果y（每人每个）与x（个）之间的函数关系式为 ．
14．某校科技小组进行野外考察，利用铺垫木板的方式通过了一片烂泥湿地，这是因为人和木板对湿地的压力一定时，人和木板对地面的压强与木板面积存在函数关系：（如图所示）．若木板面积为则压强为 ．
15．小王驾车从甲地到乙地，他以70千米/时的平均速度4小时到达目的地，当他按原路匀速返回甲地时，汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为 ．
16．一定质量的氧气，它的密度是它的体积的反比例函数．当时，，则ρ与V的函数关系是 ．
17．一司机驾驶汽车从甲地去乙地，他以80km/h的速度匀速行驶2小时到达乙地，当他按原路匀速返回甲地时，汽车的速度v（km/h）与时间t（h）的函数关系为 ．
18．已知三角形的面积是定值S，则三角形的高h与底a的函数关系式是h＝ ，这时h是a的 函数．
19．某商场出售一批进价为2元的贺卡，在市场营销中发现此贺卡的日销售单价x（元）与日销售量y（个）之间有如下关系：
则y与x之间的函数关系式为 ．
20．小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200 N和0.5m,当撬动石头的动力F至少需要400N时,则动力臂l的最大值为 m.
三、解答题
21．在平面直角坐标系中，已知反比例函数y＝的图象经过点A(1，)．
(1)试确定此反比例函数的解析式；
(2)点O是坐标原点，将线OA绕O点顺时针旋转30°得到线段OB，判断点B是否在此反比例函数的图象上，并说明理由．
22．在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，二氧化碳的密度也会随之改变，密度（单位：kg/m3）是体积V（单位：m3）的反比例函数，它的图象如图所示．
(1)求与V之间的函数关系式：
(2)求当m3时二氧化碳的密度．
23．如图，在平面直角坐标系xOy内，函数y＝的图象与反比例函数y＝（k≠0）图象有公共点A，点A的坐标为（8，a），AB⊥x轴，垂足为点B．
（1）求反比例函数的解析式；
（2）点P在线段OB上，若AP＝BP+2，求线段OP的长；
（3）点D为射线OA上一点，在（2）的条件下，若S△ODP＝S△ABO，求点D的坐标．
24．阅读与应用：同学们，你们已经知道()2，即2b2所以2b2当且仅当时取等号．
阅读：若、为实数，且，，，，当且仅当时取等号．
阅读：若函数为常数由阅读结论可知：，即当即，时，函数的最小值为．
阅读理解上述内容，解答下列问题：
问题：已知一个矩形的面积为，其中一边长为，则另一边长为，周长为，当______时，矩形周长的最小值为______．
问题：若函数，则______时，函数的最小值为______．
问题3：建造一个容积为立方米，深米的长方体无盖水池，池底和池壁的造价分别为每平方米元和元，设池长为米，水池总造价为元，求当为多少时，水池总造价最低？最低是多少？
25．如图1，点A是x轴上的一个动点，过点A作x轴的垂线PA交双曲线于点P，连接OP.
（1）当点A在x轴上的正方向上运动时，的面积是否发生变化？若不变，请求出的面积；若变化，请说明理由.
（2）如图2，在x轴上点A的右侧有一点D，过点D作x轴的垂线DB交双曲线于点B，连接BO交AP于点C，设的面积为，梯形BCAD的面积为，则与的大小关系是________（选填“＞”“＝”或“＜”）
（3）如图3，PO的延长线与双曲线的另一个交点是F，作FH垂直于x轴，垂足为H，连接AF，PH，试说明四边形APHF的面积为常数.
日销售单价x（元）
…
3
4
5
6
…
日销售量y（个）
…
20
15
12
10
…
参考答案：
1．D
2．C
3．D
4．D
5．B
6．A
7．D
8．C
9．B
10．C
11．12
12．④⑤
13．y＝．
14．3000
15．y＝(x＞0)
16．ρ=
17．v＝．
18． ， 反比例
19．y=
20．1.5
21．（1）y＝；（2）在
22．(1)
(2)1kg/m3
23．（1）；（2）5；（3）
24．问题1：2，8；问题2：4，7；问题3：当时，水池总造价最低，最低为元．
25．（1）的面积不变，；（2）>；（3）见解析.