人教版九年级下册第二十六章 反比例函数26.2 实际问题与反比例函数完美版课件ppt

这是一份人教版九年级下册第二十六章 反比例函数26.2 实际问题与反比例函数完美版课件ppt，共13页。PPT课件主要包含了典例练习，阻力臂，动力臂，4×1026，新知探究，巩固提升，知识小结，与其他知识的综合，思想方法小结，与力学的综合等内容，欢迎下载使用。

反比例函数在数学中的应用
反比例函数在物理中的应用
反比例函数在生活中的应用
【例1】码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天. (1)轮船到达目的地后开始卸货,平均卸货速度v(单位：吨/天)与卸货天数t之间有怎样的函数关系？ (2)由于遇到紧急情况,要求船上的货物不超过5天卸载完毕,那么平均每天至少要卸载多少吨？
解:(1)设轮船上的货物总量为k吨,根据已知条件得k=30×8=240，
∴平均每天至少要卸载48吨.
1.矩形面积为6,它的长y与宽x之间的函数关系用图象可表示为( )
2.面积为2的直角三角形一直角边为x,另一直角边长为y,则y与x的变化规律用图象可大致表示为( ) 3.体积为20cm3 的面团做成拉面,面条的总长度y(单位：cm)与面条粗细(横截面积)S(单位：cm2)的函数关系为___________,若要使拉出来的面条粗1mm2,则面条的总长度是______cm.
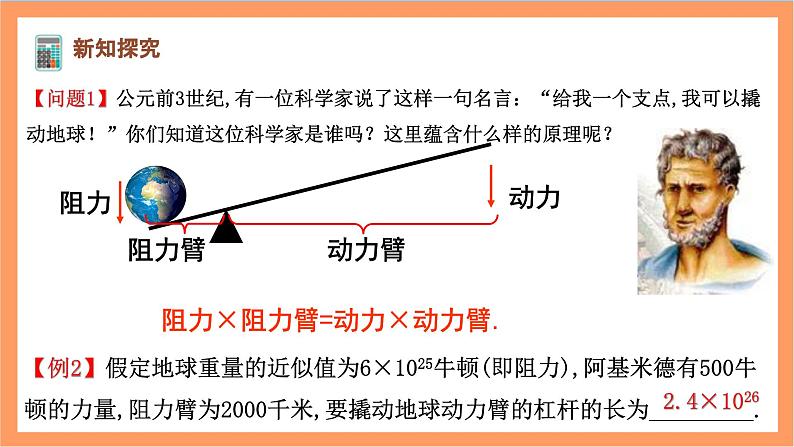
【问题1】公元前3世纪,有一位科学家说了这样一句名言：“给我一个支点,我可以撬动地球！”你们知道这位科学家是谁吗？这里蕴含什么样的原理呢？
阻力×阻力臂=动力×动力臂.
【例2】假定地球重量的近似值为6×1025牛顿(即阻力),阿基米德有500牛顿的力量,阻力臂为2000千米,要撬动地球动力臂的杠杆的长为_________.
1.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( ) A.不大于0.8m3 B.小于0.8m3 C.不小于0.8m3 D.大于0.8m32.在公式 中,当电压U一定时,电流I与电阻R之间的函数关系可用图象大致表示为( )
【例4】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中的含药量y(单位:毫克)与时间x(单位:小时)成正比例；2小时后y与x成反比例(如图).根据以上信息解答下列问题：(1)求y与x的函数解析式；(2)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长？
解：(1)当 0≤x≤2时,y与x成正比例函数关系．设y=kx,由于点(2,4)在直线上,∴4=2k,k=2,即y=2x.
当x＞2时,y与x成反比例函数关系,设y=k/x.由于点(2,4)在图象上,∴4=k/2,k=8.即y=8/x.
(2)当y=2时,x=1和x=4.
∴服药一次,治疗疾病的有效时间是4-1=3(h).
1.一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克／百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x刻画1.5时后(包括1.5时)y与x可近似地用反比例函数 (k＞0)刻画(如图).(1)根据上述数学模型计算：①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?②当x=5时,y=45.求k的值．(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”不能驾车上路.参考模型,假设某驾驶员晚上20:00在家喝照上述数学完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
∴对该材料进行特殊处理所用 的时间为
2.如图,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知第12分钟时,材料温度是14℃.(1)分别求出该材料加热和停止加热过程中y与x的函数关系式；(2)根据该食品制作要求,在材料温度不低于12℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
(2)当y=12时,y=4x+4,解得x=2.
14-2=12(分钟).
由12=168/x,解得x=14.
建模---反比例函数的数学思想方法
“杠杆原理”动力×动力臂=阻力×阻力臂
过程：分析实际情境→建立函数模型→明确数学问题
注意：实际问题中的两个变量往往都只能取非负值；作实际问题中的函数图像时,横、纵坐标的单位长度不一定相同