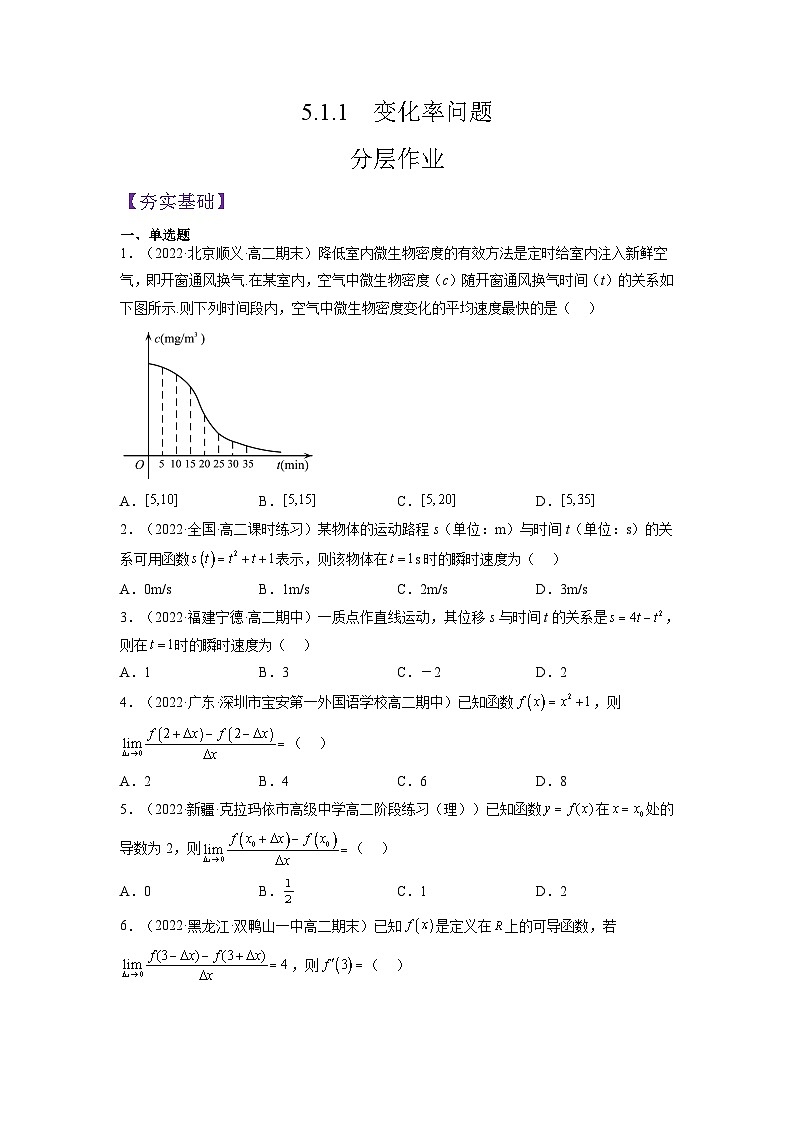
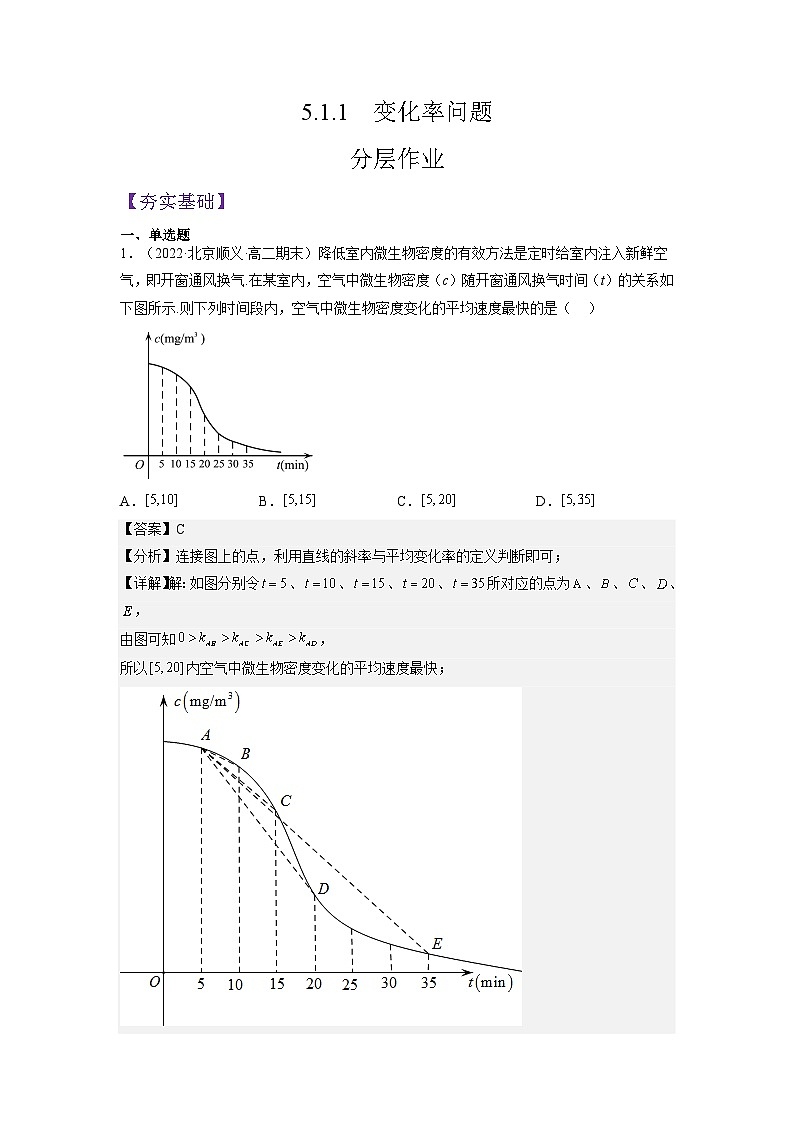
高中数学人教A版 (2019)选择性必修 第二册5.1 导数的概念及其意义课前预习课件ppt

这是一份高中数学人教A版 (2019)选择性必修 第二册5.1 导数的概念及其意义课前预习课件ppt，共16页。PPT课件主要包含了学习目标，复习回顾，平均速度，瞬时速度，物体运动的平均速度，物体运动的瞬时速度，几何意义，新课导入，不一定，与研究瞬时速度类似等内容，欢迎下载使用。

会求函数在某一点附近的平均变化率，理解函数的平均变化率，瞬时变化率及瞬时速度的概念
会求抛物线的切线斜率，体会数学的极限思想
通过本节课的学习，培养起数学抽象、逻辑推理及数学运算的核心素养.
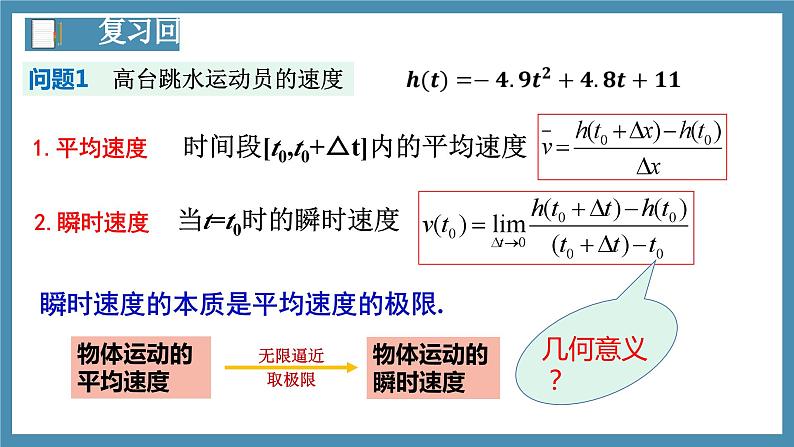
问题1 高台跳水运动员的速度
时间段[t0,t0+△t]内的平均速度
当t=t0时的瞬时速度
瞬时速度的本质是平均速度的极限.
如果一条直线与一个圆只有一个公共点，那么这条直线与这个圆相切.
对于一般的曲线C，如何定义它的切线呢？
追问1：如果一条直线与一条曲线只有一个公共点，那么这条直线与这条曲线一定相切吗？
追问2：如果一条直线与一条曲线相切，那么它们一定只有一个公共点吗？
因此，我们不能像研究直线和圆的位置关系那样，通过交点的个数来定义相切了.
新知探究：抛物线的切线斜率
问题1：如何定义抛物线 f (x)=x2 在点 P0(1,1) 处的切线？
在点P0(1,1)的附近任取一点P(x，x2)
考察抛物线f(x)＝x2的割线P0P的变化情况
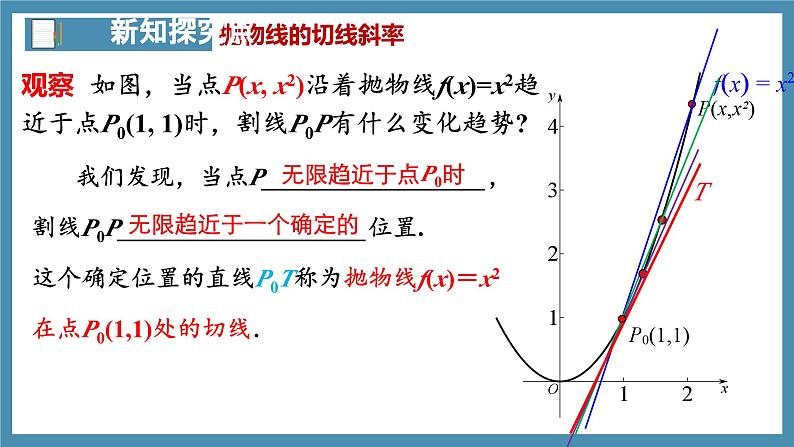
我们发现，当点P__________________，割线P0P____________________位置.这个确定位置的直线P0T称为抛物线f(x)＝x2在点P0(1,1)处的切线．
观察 如图，当点P(x, x2)沿着抛物线f(x)=x2趋近于点P0(1, 1)时，割线P0P有什么变化趋势?
记点P的横坐标x＝1＋Δx，则点P的坐标即为(1＋Δx，(1＋Δx)2).于是割线P0P的斜率
Δx→0时，斜率kP0P→2.
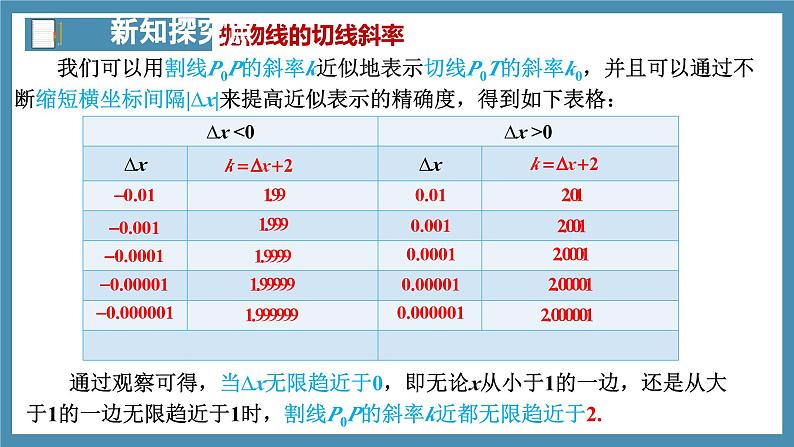
我们可以用割线P0P的斜率k近似地表示切线P0T的斜率k0，并且可以通过不断缩短横坐标间隔|∆x|来提高近似表示的精确度，得到如下表格：
通过观察可得，当∆x无限趋近于0，即无论x从小于1的一边，还是从大于1的一边无限趋近于1时，割线P0P的斜率k近都无限趋近于2.
事实上，由 可以发现，当∆x在无限趋近于0时， 无限趋近于2，我们把2叫做“当△x无限趋近于0时， 的极限”，记为
从几何图形上看，当横坐标间隔| Δx |无限变小时， 当点P无限趋近于点P0时，割线P0P无限趋近于点P0处的切线P0T . 割线P0P的斜率k 无限趋近于点P0处的切线的斜率k0. 因此，切线P0T 的斜率k0=2.
抛物线的割线及切线的斜率
函数图象在点P0(x0, f(x0))处的斜率
问题3：你能用上述方法，求抛物线 f(x)=x2在点 P0(2,4) 处的切线P0T 的斜率吗？
记点P的横坐标x＝2＋Δx，则点P的坐标即为(2＋Δx，(2＋Δx)2).于是割线P0P的斜率
故抛物线在点P0(2，4)处的切线斜率为4.
例1 求抛物线f(x)=x2+2x在点P (1, 3)处切线的斜率.
变式 求抛物线f(x)=x2+2x在点P (1, 3)处的切线方程.
1. 你认为应该怎样定义抛物线f(x)=x2在点(x0, x02)处的切线? 试求抛物线f(x)=x2在点(－1, 1)处切线的斜率.
2. 求抛物线f(x)=x2+1在点(0, 1)处的切线方程.
思考 观察问题1中的函数 的图象，平均速度 的几何意义是什么? 瞬时速度v(1)呢?