2023九年级数学上册第22章一元二次方程章末复习课件（华东师大版）

这是一份2023九年级数学上册第22章一元二次方程章末复习课件（华东师大版），共15页。

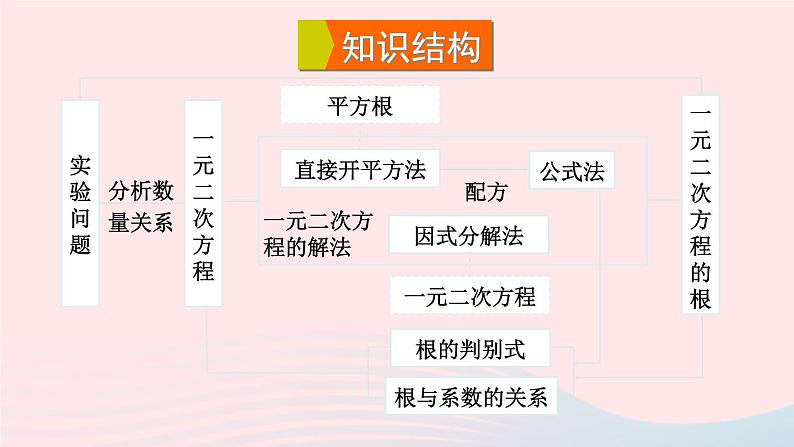
章末复习华东师大版九年级上册复习目标：掌握一元二次方程的基本概念及其解法；灵活运用一元二次方程知识解决一些实际问题.复习重点： 一元二次方程的解法及应用.复习难点： 一元二次方程的应用.实验问题一元二次方程的解法1.一元二次方程的解法平方根的定义完全平方公式配方法两个因式的积等于0，那么这两个因式至少有一个等于0x2 = p 或 (mx + n)2 = p(p ≥ 0)所有的一元二次方程所有的一元二次方程一边是0，另一边易于分解成两个一次因式的乘积的一元二次方程①②③优先选择2. 一元二次方程根的判别式 Δ = b2 – 4ac（1）当 Δ > 0 时，方程有两个不相等的实数根；（2）当 Δ = 0 时，方程有两个相等的实数根；（3）当 Δ < 0 时，方程无实数根.在应用时，要根据根的情况限定 Δ 的取值，同时应注意二次项系数不为 0 这一条件.4. 应用一元二次方程解决实际问题，要注重分析实际问题中的等量关系，列出方程，求出方程的解，同时要注意检验其是否符合题意. 用适当的方法解下列方程（1）x2 + 12x + 27 = 0 （2）x(x – 2) + x – 2 = 0（3）x2 + x – 2 = 4 （4）4(x + 2)2 = 9(2x – 1)2例1 （1）(x + 3) (x + 9) = 0x1 = – 3，x2 = – 9. （2）(x + 1)(x – 2) = 0x1 = – 1，x2 = 2.解1.用配方法解方程 x2 + 4x + 1 = 0，配方后的方程是（ ）A. (x + 2)2 = 3 B. (x – 2)2 = 3C. (x – 2)2 = 5 D. (x + 2)2 = 5A3.设 α，β 是一元二次方程 x2 + 3x – 7 = 0 的两个根，则 α2 + 4α + β = ____ . α2 + 4α + β= (α2 + 3α) + (α + β)= 7 + (–3)= 444.一学校为了绿化校园环境，向某园林公司购买了一批树苗，园林公司规定：如果购买树苗不超过 60 棵，每棵售价 120 元；如果购买树苗超过 60棵，每增加 1 棵，所出售的这批树苗每棵售价均降低 0.5 元，但每棵树苗最低售价不得少于 100 元.该校最终向园林公司支付树苗款 8800 元，请问该校共购买了多少棵树苗？解：∵60 棵树苗的售价为 120×60 = 7200（元），而 7200 < 8800，∴该校购买的树苗超过 60 棵.设该校共购买了 x 棵树苗，由题意得 x［120 – 0.5(x – 60)］ = 8800，解得 x1 = 220，x2 = 80.当 x1 = 220 时，120 – 0.5× ( 220 – 60 ) = 40 < 100，∴x = 220 不合题意，舍去；当 x2 = 80 时，120 – 0.5× ( 80 – 60 ) = 110 > 100，∴ x = 80，即该校共购买了 80 棵树苗.本堂课你能完整地回顾本章所学的有关一元二次方程的知识吗？你还有哪些困惑与疑问？本课时通过学习归纳本章内容，让学生进一步系统掌握一元二次方程的解法及其应用，让学生懂得了如何应用一元二次方程的知识来解决生活中的实际问题，激发学生的学习兴趣.