新教材2023_2024学年高中数学第5章统计与概率本章总结提升课件新人教B版必修第二册

这是一份新教材2023_2024学年高中数学第5章统计与概率本章总结提升课件新人教B版必修第二册，共37页。

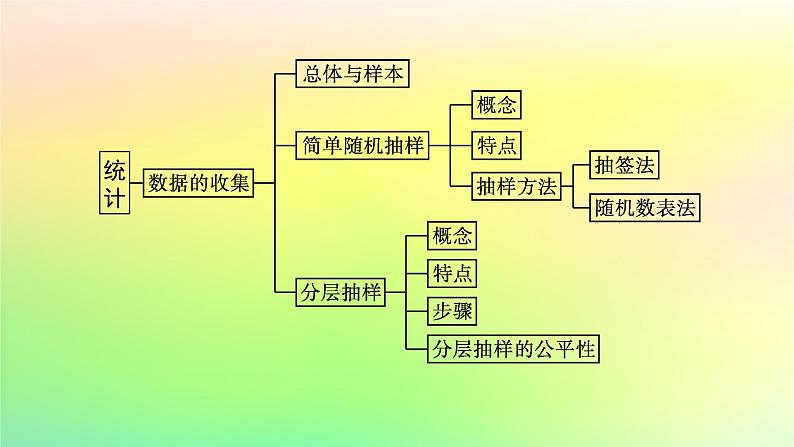
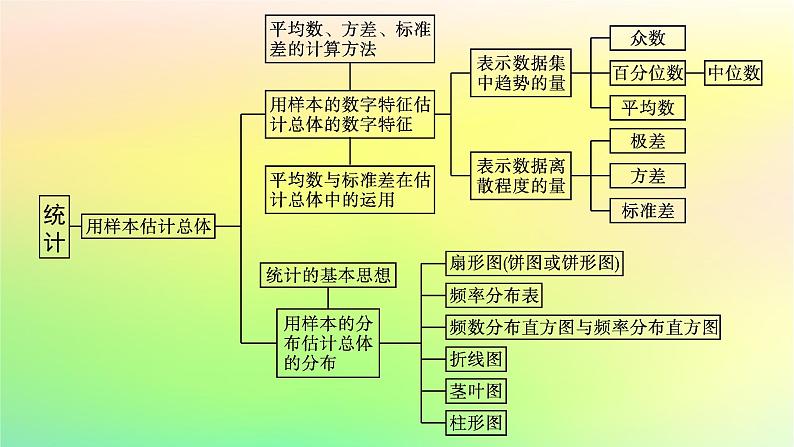
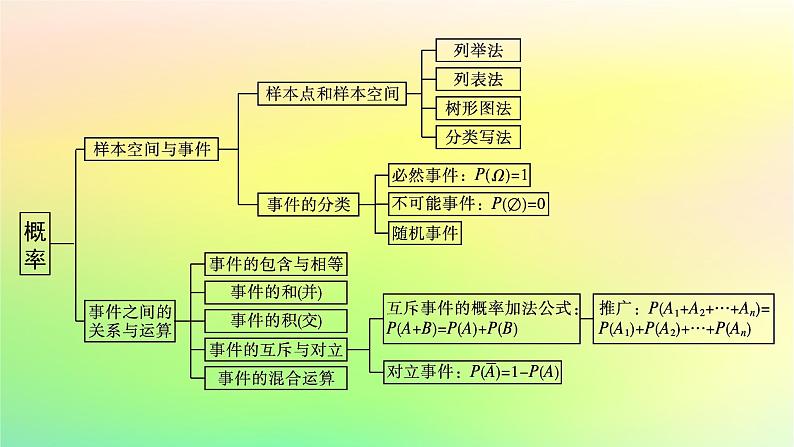
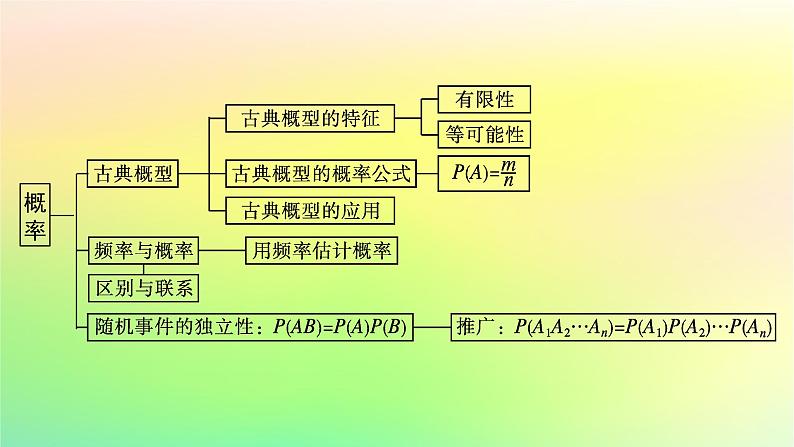
第五章本章总结提升网络构建·归纳整合专题突破·素养提升目录索引 网络构建·归纳整合专题突破·素养提升专题一　统计图表的应用1.统计图表包括柱形图、扇形图、折线图、茎叶图、频率分布直方图等,是高考的热点问题,多以选择、填空的形式考查,一般难度不大.2.掌握统计图表的应用,重点提升数据分析和数学运算素养.【例1】 [2023湖北武汉高二联考]某校100名高二学生党史竞赛成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;(2)求这100名学生党史竞赛成绩的80%分位数;(3)根据频率分布直方图,估计这100名学生党史竞赛成绩的平均分.解 (1)由频率分布直方图可得10×(2a+0.02+0.03+0.04)=1,解得a=0.005.(2)成绩落在[50,80)内的频率为(0.005+0.04+0.03)×10=0.75,落在[50,90)内的频率为(0.005+0.04+0.03+0.02)×10=0.95,故80%分位数落在[80,90),设为m,由0.75+(m-80)×0.02=0.80,得m=82.5,故80%分位数为82.5.(3)由频率分布直方图可得这100名学生党史竞赛成绩的平均分为 =(55×0.005+65×0.04+75×0.03+85×0.02+95×0.005)×10=73.规律方法　各种统计图表的应用总体分布中相应的统计图表主要包括:频率分布表、频率分布直方图、频率分布折线图等.变式训练1某学校为了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有:A.结伴步行,B.自行乘车,C.家人接送,D.其他方式. 并将收集的数据整理绘制成如图所示的两幅不完整的统计图.请根据图中信息,求本次抽查的学生中结伴步行的人数是(　　)　学生上学方式条形图　 　学生上学方式扇形图 A.30 B.40C.42 D.48A 解析 由条形图知,B.自行乘车上学的有42人,C.家人接送上学的有30人,D.其他方式上学的有18人,采用B,C,D三种方式上学的共90人,设A.结伴步行上学的有x人,由扇形图知,A.结伴步行上学与B.自行乘车上学的学生占60%,所以 ,解得x=30,故选A.专题二　数据的数字特征1.数据的数字特征可分为两大类:一类是反映数据集中趋势的,包括平均数、众数、中位数;另一类是反映数据的波动大小,包括方差和标准差.在进行数据分析时通常要将两个方面相结合进行分析.2.掌握数据的数字特征,重点提升数据分析和数学运算素养.【例2】 甲、乙两名同学数学成绩的茎叶图如图所示. (1)求出这两名同学的数学成绩的平均数、标准差;(2)比较两名同学的成绩,谈谈你的看法.所以乙同学的平均成绩较高且标准差较小,说明乙同学比甲同学的成绩扎实,稳定.规律方法　数字特征的应用样本的数字特征可分为两大类:一类反映样本数据的集中趋势,包括平均数、众数、百分位数、中位数;另一类反映样本数据的离散程度,包括极差、方差及标准差.通常,在实际问题中,仅靠平均数不能完全反映问题,还要研究方差,方差描述了数据相对于平均数的离散程度,在平均数相同的情况下,方差越大,离散程度越大,稳定性越差;方差越小,数据越集中,稳定性越好.变式训练2小明是班里的优秀学生,他的历次数学成绩分别是96分、98分、95分、93分,但最近的一次考试成绩只有45分,原因是他带病参加了考试.期末评价时,按照60~79分为“合格”,80~90分为“良好”,90~100分为“优秀”的原则,这样给小明评价:这五次数学考试的平均分是 =85.4,则按平均分给小明一个“良好”.试问这种评价是否合理?如果不合理请给出更合理的评价.解 这种评价是不合理的.尽管平均数是反映一组数据平均水平的重要特征,但任何一个数据的改变都会引起它的变化,而中位数则不受某些极端值的影响.本题中的5个成绩从小到大排列为45,93,95,96,98,中位数是95,中位数较为合理地反映了小明的数学水平,因而应该用中位数来衡量小明的数学成绩,应评定为“优秀”.专题三　古典概型1.解决古典概型的问题,关键是能分清样本空间和所求事件包含的基本事件的个数,在写相关事件时多用列举法、树状图法、图表法等.2.掌握古典概型的判断和计算,提升逻辑推理和数学运算素养.【例3】 从含有两件正品a1,a2和一件次品b的三件产品中每次任取一件,每次取出后不放回,连续取两次.(1)求取出的两件产品中恰有一件次品的概率;(2)如果将“每次取出后不放回”这一条件换成“每次取出后放回”,则取出的两件产品中恰有一件次品的概率是多少?解 (1)每次取一件,取出后不放回,则连续取两次的样本空间Ω={(a1,a2),(a1,b),(a2,a1),(a2,b),(b,a1),(b,a2)},共包含6个样本点,其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产品.可以确定这些基本事件的出现是等可能的.用A表示“取出的两件产品中恰有一件次品”,则A={(a1,b),(a2,b),(b,a1),(b,a2)},共包含4个样本点.所以(2)有放回地连续取出两件,则样本空间Ω={(a1,a1),(a1,a2),(a1,b),(a2,a1),(a2,a2),(a2,b),(b,a1),(b,a2),(b,b)},共包含9个样本点.由于每一件产品被取到的机会均等,因此可以确定这些基本事件的出现是等可能的.用B表示“取出的两件产品中恰有一件次品”,则B={(a1,b),(a2,b),(b,a1),(b,a2)},共包含4个样本点.所以P(B)= .规律方法　古典概型的应用古典概型是一种最基本的概率模型,也是学习其他概率模型的基础,在高考题中,经常出现此种概率模型的题目.解题时要紧紧抓住古典概型的两个基本特征,即有限性和等可能性.在应用公式P(A)= 时,关键是正确理解基本事件与事件A的关系,求出n,m.注意列举时必须按某一顺序做到不重不漏.变式训练3甲、乙两人参加普法知识竞赛,共有5个不同的题目.其中,选择题3个,判断题2个,甲、乙两人各抽一题.(1)甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少?(2)甲、乙两人中至少有一人抽到选择题的概率是多少?解 把3个选择题记为x1,x2,x3,2个判断题记为p1,p2.用A表示“甲抽到选择题,乙抽到判断题”,A={(x1,p1),(x1,p2),(x2,p1),(x2,p2),(x3,p1),(x3,p2)},共包含6个样本点;用B表示“甲抽到判断题,乙抽到选择题”,B={(p1,x1),(p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3)},共包含6个样本点;用C表示“甲、乙都抽到选择题”,C={(x1,x2),(x1,x3),(x2,x1),(x2,x3),(x3,x1),(x3,x2)},共包含6个样本点;用D表示“甲、乙都抽到判断题”,D={(p1,p2),(p2,p1)},共包含2个样本点.故样本空间共有20个样本点.专题四　相互独立事件的概率1.要进行相互独立事件的概率计算,先要理清事件之间的关系,借助互斥事件、对立事件、独立事件概率公式求解.2.掌握相互独立事件的概率,提升逻辑推理和数学运算素养.【例4】 甲、乙两人破译一密码,他们能破译的概率分别为 和 .求:(1)两人都能破译的概率;(2)两人都不能破译的概率;(3)恰有一人能破译的概率;(4)至多有一人能够破译的概率.规律方法　公式P(AB)=P(A)P(B)可推广到一般情形,即如果事件A1,A2,…,An相互独立,那么这n个事件同时发生的概率等于每个事件发生的概率的积,即P(A1A2…An)=P(A1)P(A2)…P(An).变式训练4[2023云南玉溪高一期末]甲、乙2人进行定点投篮游戏,在1次投篮中投进的概率分别为0.7,0.6,且各次投篮是否投进相互独立,各人投篮是否投进相互独立,每人各投篮1次为“一轮游戏”.(1)在一轮游戏中,求2人共投进1球的概率;(2)在两轮游戏中,求2人共投进1球的概率. 解 (1)记一次投篮中“甲投进”为事件A,“乙投进”为事件B,“在一轮游戏中,2人共投进1球”为事件C,