(新高考)高考数学一轮复习讲练测 第5章 第2讲　同角三角函数的基本关系与诱导公式 (2份打包，原卷版+教师版)

这是一份(新高考)高考数学一轮复习讲练测 第5章 第2讲　同角三角函数的基本关系与诱导公式 (2份打包，原卷版+教师版)，文件包含新高考高考数学一轮复习讲练测第5章第2讲同角三角函数的基本关系与诱导公式原卷版doc、新高考高考数学一轮复习讲练测第5章第2讲同角三角函数的基本关系与诱导公式原卷版pdf、新高考高考数学一轮复习讲练测第5章第2讲同角三角函数的基本关系与诱导公式教师版doc、新高考高考数学一轮复习讲练测第5章第2讲同角三角函数的基本关系与诱导公式教师版pdf等4份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。

第2讲　同角三角函数的基本关系与诱导公式


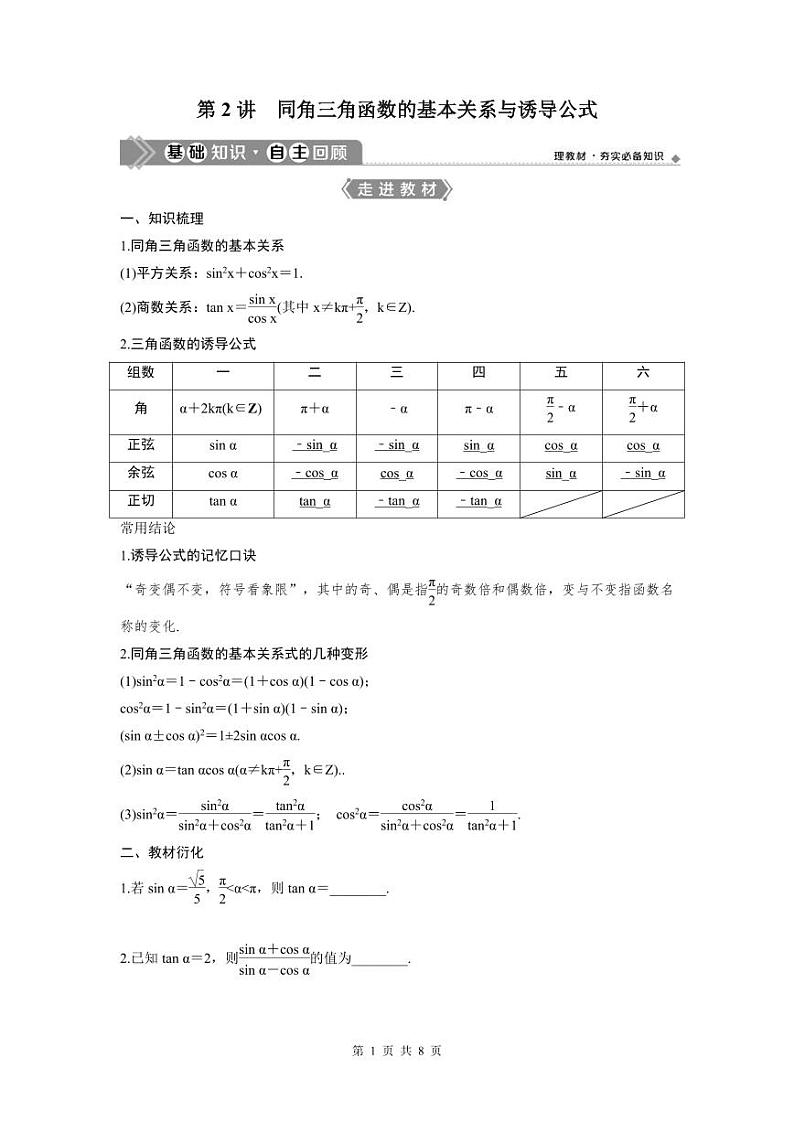
一、知识梳理
1.同角三角函数的基本关系
(1)平方关系：sin2x＋cos2x＝1.
(2)商数关系：tan x＝(其中x≠kπ+，k∈Z).
2.三角函数的诱导公式
组数
一
二
三
四
五
六
角
α＋2kπ(k∈Z)
π＋α
﹣α
π﹣α
﹣α
＋α
正弦
sin α
﹣sin_α
﹣sin_α
sin_α
cos_α
cos_α
余弦
cos α
﹣cos_α
cos_α
﹣cos_α
sin_α
﹣sin_α
正切
tan α
tan_α
﹣tan_α
﹣tan_α


常用结论
1.诱导公式的记忆口诀
“奇变偶不变，符号看象限”，其中的奇、偶是指的奇数倍和偶数倍，变与不变指函数名称的变化.
2.同角三角函数的基本关系式的几种变形
(1)sin2α＝1﹣cos2α＝(1＋cos α)(1﹣cos α)；
cos2α＝1﹣sin2α＝(1＋sin α)(1﹣sin α)；
(sin α±cos α)2＝1±2sin αcos α.
(2)sin α＝tan αcos α(α≠kπ+，k∈Z)..
(3)sin2α＝＝； cos2α＝＝.
二、教材衍化
1.若sin α＝，<α<π，则tan α＝________.
解析：因为<α<π，所以cos α＝﹣＝﹣，所以tan α＝＝﹣.
答案：﹣
2.已知tan α＝2，则的值为________.
解析：原式＝＝＝3.
答案：3
3.化简·cos(2π﹣α)的结果为________.
解析：原式＝·cos α＝sin α.
答案：sin α

一、思考辨析
判断正误(正确的打“√”，错误的打“×”)
(1)对任意的角α，β，都有sin2α＋cos2β＝1.(　　)
(2)若α∈R，则tan α＝恒成立.(　　)
(3)sin(π＋α)＝﹣sin α成立的条件是α为锐角.(　　)
(4)若cos(nπ﹣θ)＝(n∈Z)，则cos θ＝.(　　)
答案：(1)×　(2)×　(3)×　(4)×
二、易错纠偏
(1)不注意角的范围出错；
(2)诱导公式记忆不熟出错.
1.已知cos(π＋α)＝，则tan α＝(　　)
A. B. C.± D.±
解析：选C.因为cos(π＋α)＝，所以cos α＝﹣，则α为第二或第三象限角，
所以sin α＝±＝±.所以tan α＝＝＝±.
2.若sin(π＋α)＝﹣，则sin(7π﹣α)＝________，cos(α＋)＝________.
解析：由sin(π＋α)＝﹣sin α＝﹣，得sin α＝，则sin(7π﹣α)＝sin(π﹣α)＝sin α＝，
cos(α＋)＝cos(α＋﹣2π)＝cos(α﹣)＝cos(﹣α)＝sin α＝.
答案：　

考点一　同角三角函数的基本关系式(基础型)
理解同角三角函数的基本关系式：sin2x＋cos2x＝1，＝tan x.
核心素养：数学运算
角度一　“知一求二”问题
(1)已知α∈(0，π)，cos α＝﹣，则tan α＝(　　)
A. B.﹣ C. D.﹣
(2)已知α是三角形的内角，且tan α＝﹣，则sin α＋cos α的值为________.
【解析】　(1)因为cos α＝﹣且α∈(0，π)，
所以sin α＝＝，所以tan α＝＝﹣.故选D.
(2)由tan α＝﹣，得sin α＝﹣cos α，且sin α>0，cos α<0，
将其代入sin2α＋cos2α＝1，得cos2α＝1，
所以cos α＝﹣，sin α＝，故sin α＋cos α＝﹣.
【答案】　(1)D　(2)﹣

利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形.同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的.
角度二　sin α，cos α的齐次式问题
已知＝﹣1，求下列各式的值：
(1)； (2)sin2α＋sin αcos α＋2.
【解】　由已知得tan α＝.
(1)＝＝﹣.
(2)sin2α＋sin αcos α＋2＝＋2＝＋2＝.

关于sin α与cos α的齐n次分式或齐二次
整式的化简求值的解题策略
已知tan α，求关于sin α与cos α的齐n次分式或齐二次整式的值.
　
角度三　sin α±cos α，sin αcos α之间的关系
已知α∈(﹣π，0)，sin α＋cos α＝.
(1)求sin α﹣cos α的值；
(2)求的值.
【解】　(1)由sin α＋cos α＝，
平方得sin2α＋2sin αcos α＋cos2α＝，整理得2sin αcos α＝﹣.
所以(sin α﹣cos α)2＝1﹣2sin αcos α＝.
由α∈(﹣π，0)，知sin α<0，又sin α＋cos α>0，
所以cos α>0，则sin α﹣cos α<0，故sin α﹣cos α＝﹣.
(2)＝＝＝﹣.


sin α±cos α与sin αcos α关系的应用技巧
(1)通过平方，sin α＋cos α，sin α﹣cos α，sin αcos α之间可建立联系，若令sin α＋cos α＝t，则sin αcos α＝，sin α﹣cos α＝±(注意根据α的范围选取正、负号).
(2)对于sin α＋cos α，sin α﹣cos α，sin αcos α这三个式子，可以知一求二.

1.已知sin αcos α＝，且<α<，则cos α﹣sin α的值为(　　)
A.﹣ B. C.﹣ D.
解析：选B.因为<α<，所以cos α<0，sin α<0且|cos α|<|sin α|，所以cos α﹣sin α>0.又(cos α﹣sin α)2＝1﹣2sin αcos α＝1﹣2×＝，所以cos α﹣sin α＝.故选B.
2.若3sin α＋cos α＝0，则的值为________.
解析：3sin α＋cos α＝0⇒cos α≠0⇒tan α＝﹣，
＝＝＝.
答案：
3.已知θ为第四象限角，sin θ＋3cos θ＝1，则tan θ＝________.
解析：由(sin θ＋3cos θ)2＝1＝sin2θ＋cos2θ，得6sin θcos θ＝﹣8cos2θ，又因为θ为第四象限角，所以cos θ≠0，所以6sin θ＝﹣8cos θ，所以tan θ＝﹣.
答案：﹣
考点二　诱导公式的应用(基础型)
借助单位圆中的三角函数线推导出诱导公式(± α，π± α的正弦、余弦、正切).
核心素养：数学运算
(1)sin(﹣1 200°)cos 1 290°＝________.
(2)已知角θ的顶点在坐标原点，始边与x轴正半轴重合，终边在直线3x﹣y＝0上，则等于________.
【解析】　(1)原式＝﹣sin 1 200°cos 1 290°
＝﹣sin(3×360°＋120°)cos(3×360°＋210°)
＝﹣sin 120°cos 210°
＝﹣sin(180°﹣60°)cos(180°＋30°)
＝sin 60°cos 30°＝×＝.
(2)由题可知tan θ＝3，原式＝＝＝.
【答案】　(1)　(2)
【迁移探究】　(变问法)若本例(2)的条件不变，则＝________.
解析：由题可知tan θ＝3，
原式＝＝
＝＝＝＝3.
答案：3

(1)诱导公式用法的一般思路
①化负为正，化大为小，化到锐角为止；
②角中含有加减的整数倍时，用公式去掉的整数倍.
(2)常见的互余和互补的角
①常见的互余的角：﹣α与＋α；＋α与﹣α；＋α与﹣α等；
②常见的互补的角：＋θ与﹣θ；＋θ与﹣θ等.

1.已知α∈(0，π)，且cos α＝﹣，则sin(＋α)·tan(π＋α)＝(　　)
A.﹣ B. C.﹣ D.
解析：选D.sin(＋α)·tan(π＋α)＝cos α·tan α＝sin α，因为α∈(0，π)，且cos α＝﹣，
所以sin α＝ ＝ ，即sin(＋α)·tan(π＋α)＝.故选D.
2.已知sin(α﹣)＝，则cos的值等于________.
解析：由sin(α﹣)＝，得cos＝cos＝sin(α﹣)＝.
答案：
考点三　基本关系式与诱导公式的综合应用(综合型)
利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形.
(1)已知α为锐角，且2tan(π﹣α)﹣3cos(+β)＋5＝0，tan(π＋α)＋6sin(π＋β)﹣1＝0，则sin α的值是(　　)
A. B. C. D.
(2)已知α是第三象限角，且f(α)＝.
①化简f(α)；
②若tan(π﹣α)＝﹣2，求f(α)的值；
③若α＝﹣420°，求f(α)的值.
【解】　(1)选C.由已知可得﹣2tan α＋3sin β＋5＝0，tan α﹣6sin β﹣1＝0，解得tan α＝3，又α为锐角，故sin α＝.
(2)①由题可得，
f(α)＝＝＝﹣cos α.
②因为tan(π﹣α)＝﹣2，所以tan α＝2.所以sin α＝2cos α.
所以(2cos α)2＋cos2α＝1.所以cos2α＝.
因为α是第三象限角，所以cos α＝﹣，所以f(α)＝.
③因为cos (﹣420°)＝cos 420°＝cos 60°＝，
所以f(α)＝﹣cos α＝﹣.

求解诱导公式与同角关系综合问题的
基本思路和化简要求
基本思路
①分析结构特点，选择恰当公式；
②利用公式化成单角三角函数；
③整理得最简形式
化简要求
①化简过程是恒等变换；
②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值

1.已知tan(﹣2 019π＋θ)＝﹣2，则2sin(θ﹣)sin(θ＋)＝(　　)
A.﹣2 B. C. D.
解析：选B.因为tan(﹣2 019π＋θ)＝﹣2，所以tan θ＝﹣2.
则2sin(θ﹣)sin(θ＋)＝(sin θ﹣cos θ)(sin θ＋cos θ)
＝sin2θ﹣cos2θ＋(﹣1)sin θcos θ＝
＝＝＝.故选B.
2.已知函数f(x)＝asin(πx＋α)＋bcos(πx＋β)，且f(4)＝3，则f(2 019)的值为________.
解析：因为f(x)＝asin(πx＋α)＋bcos(πx＋β)，
所以f(4)＝asin(4π＋α)＋bcos(4π＋β)＝asin α＋bcos β＝3，
所以f(2 019)＝asin(2 019π＋α)＋bcos(2 019π＋β)
＝asin(π＋α)＋bcos(π＋β)＝﹣asin α﹣bcos β＝﹣3.
答案：﹣3

[基础题组练]
1.计算：sin ＋cos ＝(　　)
A.﹣1 B.1 C.0 D.﹣
解析：选A.原式＝sin(2π﹣)＋cos(3π+)＝﹣sin ＋cos(π+)＝﹣﹣cos ＝﹣﹣＝﹣1.


2.(多选)若角A，B，C是△ABC的三个内角，则下列等式中一定成立的是(　　)
A.cos(A＋B)＝cos C B.sin(A＋B)＝﹣sin C
C.cos＝sin D.sin＝cos
解析：选CD.因为A＋B＋C＝π，所以A＋B＝π﹣C，＝，＝，
所以cos(A＋B)＝cos(π﹣C)＝﹣cos C，sin(A＋B)＝sin(π﹣C)＝sin C，
cos＝cos(﹣)＝sin ，sin＝sin(﹣)＝cos.
3.已知sin(π＋θ)＝﹣cos(2π﹣θ)，|θ|＜，则θ等于(　　)
A.﹣ B.﹣ C. D.
解析：选D.因为sin(π＋θ)＝﹣cos(2π﹣θ)，所以﹣sin θ＝﹣cos θ，
所以tan θ＝，因为|θ|＜，所以θ＝.
4.已知f(α)＝，则f()＝(　　)
A. B. C. D.﹣
解析：选A.f(α)＝＝＝＝cos α，
则f()＝cos＝.
5.已知sin α＋cos α＝，则tan α＋的值为(　　)
A.﹣1 B.﹣2 C. D.2
解析：选D.因为sin α＋cos α＝，所以(sin α＋cos α)2＝2，所以sin αcos α＝.
所以tan α＋＝＋＝＝2.故选D.
6.设α是第三象限角，tan α＝，则cos(π﹣α)＝________.
解析：因为α为第三象限角，tan α＝，所以cos α＝﹣，所以cos(π﹣α)＝﹣cos α＝.
答案：
7.已知sin(﹣﹣α)cos(﹣π+α)＝，且0＜α＜，则sin α＝________，cos α＝________.
解析：sin(﹣﹣α)cos(﹣π+α)＝﹣cos α·(﹣sin α)＝sin αcos α＝.
因为0＜α＜，所以0＜sin α＜cos α.
又因为sin2α＋cos2α＝1，所以sin α＝，cos α＝.
答案：　
8.化简＝________.
解析：原式＝
＝＝＝＝1.
答案：1
9.已知α为第三象限角，
f(α)＝.
(1)化简f(α)；
(2)若cos(α﹣)＝，求f(α)的值.
解：(1)f(α)＝
＝＝﹣cos α.
(2)因为cos(α﹣)＝，所以﹣sin α＝，
从而sin α＝﹣.又α为第三象限角，
所以cos α＝﹣＝﹣，
所以f(α)＝﹣cos α＝.
10.是否存在α∈(﹣,)，β∈使等式sin(3π﹣α)＝cos(﹣β)，cos(﹣α)＝﹣cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由.
解：假设存在角α，β满足条件.
由已知条件可得
由①2＋②2，得sin2α＋3cos2α＝2.
所以sin2α＝，所以sin α＝±.
因为α∈(﹣,)，所以α＝±. 当α＝时，由②式知cos β＝，
又β∈(0，π)，所以β＝，此时①式成立；
当α＝﹣时，由②式知cos β＝，又β∈(0，π)，所以β＝，此时①式不成立，故舍去.
所以存在α＝，β＝满足条件.
[综合题组练]
1.已知θ为直线y＝3x﹣5的倾斜角，若A(cos θ，sin θ)，B(2cos θ＋sin θ，5cos θ﹣sin θ)，则直线AB的斜率为(　　)
A.3 B.﹣4 C. D.﹣
解析：选D.由题意知tan θ＝3，kAB＝＝＝﹣.故选D.
2.A＝{sin α，cos α，1}，B＝{sin2α，sin α＋cos α，0}，且A＝B，则sin2 019α＋cos2 018α＝(　　)
A.0 B.1 C.﹣1 D.±1
解析：选C.当sin α＝0时，sin2α＝0，此时集合B中不符合集合元素的互异性，故舍去；当cos α＝0时，A＝{sin α，0，1}，B＝{sin2α，sin α，0}，此时sin2α＝1，得sin α＝﹣1，所以sin2 019α＋cos2 018α＝﹣1.
3.若|sin θ|＋|cos θ|＝，则sin4θ＋cos4θ＝________.
解析：|sin θ|＋|cos θ|＝，两边平方得，1＋|sin 2θ|＝，所以|sin 2θ|＝，所以sin4θ＋cos4θ＝(sin2θ＋cos2θ)2﹣2sin2θcos2θ＝1﹣2sin2θcos2θ＝1﹣sin2 2θ＝.
答案：
4.若k∈Z时，的值为________.
解析：当k为奇数时，
＝＝﹣1；
当k为偶数时，
＝＝﹣1.
答案：﹣1
5.已知关于x的方程2x2﹣(＋1)x＋m＝0的两根分别是sin θ和cos θ，θ∈(0，2π)，求：
(1)＋的值；
(2)m的值；
(3)方程的两根及此时θ的值.
解：(1)原式＝＋
＝＋
＝＝sin θ＋cos θ.
由条件知sin θ＋cos θ＝，
故＋＝.
(2)由已知，得sin θ＋cos θ＝，sin θcos θ＝，
又1＋2sin θcos θ＝(sin θ＋cos θ)2，可得m＝.
(3)由得或
又θ∈(0，2π)，故θ＝或θ＝.




6.在△ABC中，
(1)求证：cos2＋cos2 ＝1；
(2)若cos(+A)sin(+B)tan(C﹣π)＜0，
求证：△ABC为钝角三角形.
证明：(1)在△ABC中，A＋B＝π﹣C，
所以＝﹣，
所以cos＝cos(﹣)＝sin ，
所以cos2＋cos2＝1.
(2)若cos(+A)sin(+B)tan(C﹣π)＜0，
所以(﹣sin A)(﹣cos B)tan C＜0，
即sin Acos Btan C＜0.
因为在△ABC中，0＜A＜π，0＜B＜π，0＜C＜π且sin A＞0，
所以或
所以B为钝角或C为钝角，所以△ABC为钝角三角形.