数学九年级上册3.公式法教学设计

3.公式法

※教学目标※

【知识与技能】

1.理解一元二次方程求根公式的推导过程.

2.会用求根公式解简单数字系数的一元二次方程.

【过程与方法】

经历探索求根公式的过程，发展学生的合情推理能力，提高学生的运算能力并养成良好的运算习惯.

【情感态度】

通过运用公式法解一元二次方程的训练，提高学生的运算能力，并让学生在学习中获得成功的体验，建立学好数学的自信心.

【教学重点】

掌握一元二次方程的求根公式，并能用它熟练地解一元二次方程.

【教学难点】

一元二次方程求根公式的推导过程.

※教学过程※

一、复习引入

1.教师引导学生回忆配方法解一元二次方程的一般步骤.

2.用直接开平方法和配方法解一元二次方程，计算比较麻烦，能否研究出一种更好的方法，迅速求得一元二次方程的实数根呢？

二、探索新知

1.一元二次方程求根公式的推导过程：

解一般形式的一元二次方程：

解：系数化为1，得

移项，得

配方，得

即

因为时，直接开平方，得

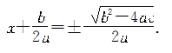
所以

即

2.一元二次方程的求根公式：

将一元二次方程中系数a、b、c的值，直接代入这个公式，就可以求得方程的根.这种解一元二次方程的方法叫做公式法.

【例1】  解下列方程：

分析：对于（2）、（4）首先要把方程化成一般形式；注意a、b、c的符号；先计算的值，再代入公式求解较简便.

解：

所以

即

(2)将方程化为一般形式，得

因为

所以

即

(3)因为

所以

即

(4)整理,得

因为

所以

即

注意：此方程的解不能写成,不要误认为只有一个实数根，而是有两个相等的实数根.

【例2】  解方程：

解：因为

所以方程无实数解.

说明：当时，不用代入求根公式，直接写出方程无实数根即可.

三、巩固练习

用公式法解下列方程：

答案：



四、归纳小结

1.用公式法解一元二次方程的两个前提条件：一是

2.当时，方程有两个相等的实数根，不要误认为只有一个实数根.

3.当时，直接写此方程无实数根即可.

※课后作业※

教材习题22.2第3题（2），第4题（1）、（2）、（3）、（6）.