初中数学湘教版八年级下册4.5 一次函数的应用同步训练题

[一次函数与方案决策]

一、选择题

1.某地打长途电话3分钟之内收费1.8元,3分钟以后每增加1分钟加收0.5元,当通话时间t不小于3分钟时,电话费y(元)与通话时间t(分)之间的表达式为              (　　)

A.y=t+2.4　　  B.y=0.5t+1　

C.y=0.5t+0.3　  D.y=0.5t-0.3

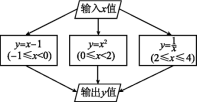
2.根据如图所示的程序计算函数值,若输入的x值为,则输出的y值为 (　　)

A.　 B.　 C.　 D.

3.(2021益阳模拟)某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费.若某乘客有一次乘出租车的车费为36元,则这位乘客乘车的里程为              (　　)

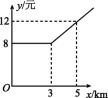
A.10 km B.14 km C.15 km D.17 km

二、填空题

4.某书的定价为25元/本,如果一次性购买20本以上,超过20本的部分打八折,试写出付款金额y(单位:元)与购书数量x(单位:本)之间的函数表达式:　　　　　　　　　.               

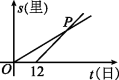
5.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”图是两匹马行走的路程s关于行走时间t的函数图象,则两图象交点P的坐标是　　　　. 

三、解答题

6.(2021张家界模拟)某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费:

月用水量不超过20 m3时,按2.5元/m3计费;月用水量超过20 m3时,其中20 m3仍按2.5元/m3收费,超过部分按3.2元/m3计费.设每户家庭月用水量为x m3时,应交水费y元.

(1)分别写出当0≤x≤20和x>20时,y与x之间的函数表达式;

(2)小明家第二季度缴纳水费的情况如下:

小明家第二季度共用水多少立方米?

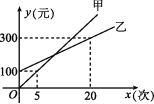
7.某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x之间的函数关系如图所示,解答下列问题:

(1)分别求出选择这两种卡消费时,y关于x的函数表达式;

(2)请根据入园次数确定选择哪种卡消费比较合算.

8.新农村社区改造过程中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元.已知该楼盘每套楼房面积均为120平方米.

若购买者一次性付清所有房款,开发商有两种优惠方案:

方案一:降价8%,另外每套楼房赠送a元装修基金;

方案二:降价10%,没有其他赠送.

(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数表达式;

(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.

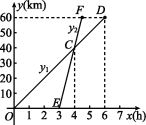
 [数形结合] 已知A,B两地相距60 km,甲骑自行车,乙骑摩托车沿同一条笔直的公路由A地匀速行驶到B地.设行驶时间为x(h),甲、乙两人离开A地的路程分别记为y1(km),y2(km),它们与x(h)的关系如图所示.

(1)线段OD所在直线的函数表达式是　　　　,线段EF所在直线的函数表达式是　　　　; 

(2)试求点F的坐标,并说明其实际意义;

(3)乙在行驶过程中,求两人距离超过6 km时x的取值范围.

答案

1.C

2. A　因为x的值为,所以根据自变量的取值范围,选用第三个函数表达式进行计算,得结果为.

3. D　由图象得出租车的起步价是8元;设当x>3时,y与x之间的函数关系式为y=kx+b.由函数图象,得解得

故y与x之间的函数关系式为y=2x+2.

∵36>8,

∴令y=36,则36=2x+2,解得x=17.

4.y=

5. (32,4800)

 由题意,得150t=240(t-12),解得t=32,则150t=150×32=4800,

∴点P的坐标为(32,4800).

6.解:(1)当0≤x≤20时,y与x之间的函数表达式是y=2.5x;

当x>20时,y与x之间的函数表达式是

y=2.5×20+3.2(x-20)=3.2x-14.

(2)小明家用水量x=20时,水费y=2.5×20=50(元).

因为小明家四、五月份的水费都不超过50元,故满足y=2.5x;

六月份的水费超过50元,故满足y=3.2x-14.

把y=40代入y=2.5x中,得2.5x=40,

解得x=16;

把y=45代入y=2.5x中,得2.5x=45,

解得x=18;

把y=56.4代入y=3.2x-14中,得3.2x-14=56.4,解得x=22.16+18+22=56(m3),

故小明家第二季度共用水56 m3.

7.解:(1)设选择甲种消费卡时,y关于x的函数表达式为y甲=k1x.根据题意,得5k1=100,解得k1=20,∴选择甲种消费卡时,y关于x的函数表达式为y甲=20x(x≥0,且x为整数);

设选择乙种消费卡时,y关于x的函数表达式为y乙=k2x+100.根据题意,得20k2+100=300,解得k2=10,∴选择乙种消费卡时,y关于x的函数表达式为y乙=10x+100(x≥0,且x为整数).

(2)结合(1)得:①当y甲<y乙,即20x<10x+100时,x<10,所以当入园次数小于10次时,选择甲消费卡比较合算;

②当y甲=y乙,即20x=10x+100时,x=10,所以当入园次数等于10次时,选择两种消费卡费用一样;

③当y甲>y乙,即20x>10x+100时,x>10,所以当入园次数大于10次时,选择乙消费卡比较合算.

8.解:(1)当1≤x≤8,x为整数时,y=4000-30(8-x)=30x+3760;

当8<x≤23,x为整数时,y=4000+50(x-8)=50x+3600.

所以售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数表达式为

y=

(2)当x=16时,y=50×16+3600=4400,

总价为4400×120=528000(元).

方案一需付房款:[528000×(1-8%)-a]元;

方案二需付房款:528000×(1-10%)元.

令528000×(1-8%)-a=528000×(1-10%),解得a=10560,

所以当a<10560时,选择方案二更合算;当a=10560时,两种方案均可;当a>10560时,选择方案一更合算.

[素养提升]

解:(1)y1=10x　y2=40x-120　 设线段OD所在直线的函数表达式为y1=kx.

根据题意,得6k=60,解得k=10,

∴线段OD所在直线的函数表达式为y1=10x,

∴点C的纵坐标为4×10=40.

设线段EF所在直线的函数表达式为y2=k1x+b.根据题意,得

解得

∴线段EF所在直线的函数表达式为y2=40x-120.

(2)令40x-120=60,

解得x=4.5,

∴点F的坐标为(4.5,60).

点F的实际意义为乙骑摩托车出发1.5小时后到达B地.

(3)当10x-(40x-120)>6时,解得x<3.8,即3≤x<3.8时,乙在行驶过程中,两人距离超过6 km;

当40x-120-10x>6时,解得x>4.2,即4.2<x≤4.5时,乙在行驶过程中,两人距离超过6 km.

故乙在行驶过程中,两人距离超过6 km时x的取值范围为3≤x<3.8或4.2<x≤4.5.