初中数学人教版九年级上册22.3 实际问题与二次函数精练

22.3实际问题与二次函数专题训练（4大题型35题）

题型1：几何问题-面积问题

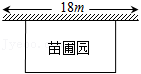
1．某中学课外兴趣活动小组准备围建一个矩形苗圃园（如图所示），其中一边靠墙（墙长为18m），另外三边用32m的篱笆围成．

（1）令苗圃园长（平行于墙的边长）为xm，宽为ym，写出y关于x的函数关系式，并写出x的取值范围；

（2）若苗圃园的面积为96m2，求垂直于墙的一边长为多少米？

（3）苗圃园的面积能否达到150m2？请说明理由；并写出苗圃园的面积最大值．

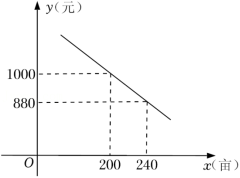
2．目前世界上有10亿多人以马铃薯为主粮，为国家粮食安全，丰富农民收入来源，某区试点马铃薯种植，给予每亩地每年发放150元补贴．年初，种植户金大伯根据以往经验，考虑各种因素，预计本年每亩的马铃薯销售收入为2000元，以及每亩种植成本y（元）与种植面积x（亩）之间的函数关系如图所示．

（1）根据图象，求出y与x之间的函数关系式．

（2）根据预计情况，求金大伯今年种植总收入w（元）与种植面积x（亩）之间的函数关系式．（总收入＝销售收入﹣种植成本+种植补贴）．

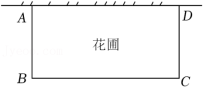
3．如图，学校要用一段长为36米的篱笆围成一个一边靠墙的矩形花圃，墙长为16米．

（1）若矩形ABCD的面积为144平方米，求矩形的边AB的长．

（2）要想使花圃的面积最大、AB边的长应为多少米？最大面积为多少平方米？

4．数学课外活动小组进行如下操作实验，把一根长20m的铁丝剪成两段．

（1）把每段首尾相连各围成一个正方形．要使这两个正方形的面积之和等于13m2，应该怎么剪这根铁丝？

（2）若把剪成两段的铁丝围成两个圆，两圆面积之和的最小值是多少？

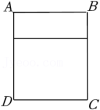
5．如图，用一根60厘米的铁丝制作一个“日”字型框架ABCD，铁丝恰好全部用完．

（1）若所围成的矩形框架ABCD的面积为144平方厘米，则AB的长为多少厘米？

（2）矩形框架ABCD面积的最大值为 　   　平方厘米．

6．园林部门计划在某公园建一个长方形苗圃ABCD．苗圃的一面靠墙（墙最大可用长度为14米）．另三边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并在如图所示的两处各留2米宽的门（门不用木栏），建成后所用木栏总长32米，设苗圃ABCD的一边CD长为x米．

（1）BC长为 　       　米（包含门宽，用含x的代数式表示）；

（2）若苗圃ABCD的面积为96m2，求x的值；

（3）当x为何值时，苗圃ABCD的面积最大，最大面积为多少？

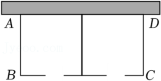
7．为了提高巴中市民的生活质量，巴中市对老旧小区进行了美化改造．如图，在老旧小区改造中，某小区决定用总长27m的栅栏，再借助外墙围成一个矩形绿化带ABCD，中间用栅栏隔成两个小矩形，已知房屋外墙长9m．

（1）当AB长为多少时，绿化带ABCD的面积为42m2？

（2）当AB长为多少时，绿化带ABCD的面积最大，最大面积是多少？

8．如图，若要建一个矩形场地，场地的一面靠墙，墙长10m，另三边用篱笆围成，篱笆总长20m，设垂直于墙的一边为xm，矩形场地的面积为Sm2．

（Ⅰ）S与x的函数关系式为S＝　       　，其中x的取值范围是 　       　；

（Ⅱ）若矩形场地的面积为42m2，求矩形场地的长与宽；

（Ⅲ）当矩形场地的面积最大时，求矩形场地的长与宽，并求出矩形场地面积的最大值．

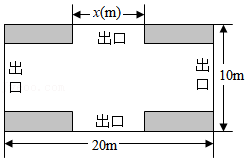
9．在校园嘉年华中，九年级同学将对一块长20m，宽10m的场地进行布置，设计方案如图所示．阴影区域为绿化区（四块全等的矩形），空白区域为活动区，且4个出口宽度相同，其宽度不小于4m，不大于8m．设出口长均为x（m），活动区面积为y（m2）．

（1）求y关于x的函数表达式；

（2）当x取多少时，活动区面积最大？最大面积是多少？

（3）若活动区布置成本为10元/m2，绿化区布置成本为8元/m2，布置场地的预算不超过1850元，当x为整数时，请求出符合预算且使活动区面积最大的x值及此时的布置成本．

题型2：几何问题-动点问题

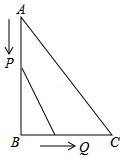
10．如图，在Rt△ABC中，∠B＝90°，AB＝3cm，BC＝4cm，点P从点A出发，以1cm/s的速度沿AB运动；同时，点Q从点B出发，以2cm/s的速度沿BC运动．当点Q到达点C时，P、Q两点同时停止运动．设运动时间为t（s），四边形APQC的面积为S（cm）．

（1）试写出四边形APQC的面积为S（cm）与动点运动时间t之间的函数表达式；

（2）运动时间t为何值时，四边形APQC的面积最小？最小值为多少？

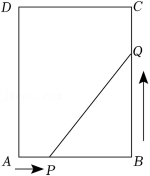
11．如图，在矩形ABCD中，AB＝10cm，BC＝16cm，点P从点A开始沿边AB向点B以2cm/s的速度移动，点Q以点B开始沿边BC向点C以3cm/s的速度移动，如果P、Q分别从A、B同时出发，当一点到达终点时，另一个点随即停止移动．

（1）经过几秒，△PBQ的面积等于18cm2？

（2）在运动过程中，经过几秒时，△PBQ的面积最大？最大面积是多少？

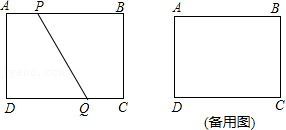
12．在长方形ABCD中，AB＝3，BC＝4，动点P从点A开始按A→B→C→D的方向运动到点D．如图，设动点P所经过的路程为x，△APD的面积为y．（当点P与点A或D重合时，y＝0）

（1）写出y与x之间的函数解析式；

（2）直接写出△APD的面积的最大值．

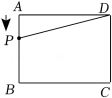
13．如图，在△ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P从点A开始沿边AB向点B以2cm/s的速度移动，动点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果P、Q两点分别从A，B两点同时出发，设运动时间为t，

（1）AP＝　2tcm　，BP＝　（12﹣2t）cm　，BQ＝　4tcm　；

（2）t为何值△时△PBQ的面积为32cm2？

（3）t为何值时△PBQ的面积最大？最大面积是多少？

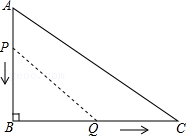
14．如图，在Rt△ABC中，∠C＝90°，AC＝12cm，BC＝6cm，点P从点C开始沿CB向点B以1cm/s的速度移动，点Q从A开始沿AC向点C以2cm/s的速度移动，如果点P，Q同时从点C，A出发，试问：

（1）出发多少时间时，点P，Q之间的距离等于？

（2）出发多少时间时，△PQC的面积为6cm2？

（3）△PQC面积的是否有最大值？若有是多少？此时时间是多少？

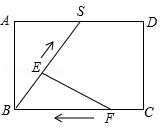
15．如图，在矩形ABCD中，BC＝6cm，AB＝4cm，S是AD中点，点E以每秒2cm的速度从点B出发沿折线BS﹣SD﹣DC匀速运动，同时点F以每秒1cm的速度从点C出发沿CB运动．设点E、F出发t秒（0＜t＜6）时，△EBF的面积为ycm2．

（1）求y与t的函数关系式；

（2）当t为何值时，y取得最大值，并求出此最大值．

16．如图，在Rt△AOB中，∠AOB＝90°，且AO＝8，BO＝6，P是线段AB上一个动点，PE⊥AO于E，PF⊥BO于F．设

PE＝x，矩形PFOE的面积为S

（1）求出S与x的函数关系式；

（2）当x为何值时，矩形PFOE的面积S最大？最大面积是多少？

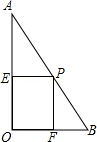
17．如图，在矩形ABCD中，AB＝8，AD＝6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP＝CQ．设AP＝x．

（1）当PQ∥AD时，求x的值；

（2）当线段PQ的垂直平分线与BC边相交时，求x的取值范围；

（3）当线段PQ的垂直平分线与BC相交时，设交点为E，连接EP、EQ，设△EPQ的面积为S，求S关于x的函数关系式，并写出S的取值范围．

题型3：利润问题

18．某种产品按质量不同分等级，生产最低档次产品每件获利润8元，每提高一个档次，每件利润增加2元．用同样工时每天可生产最低档次产品800件，每提高一个档次将减产40件，求生产何种档次产品的利润最高？

19．小明在“生活中的数学”探究活动中，经过市场调查，研究了某种商品的售价、销量、利润之间的变化关系．小明整理出该商品的相关数据如下表所示．

已知该商品的进价为每件10元，设销售该商品的每天利润为y元．

（1）求y与x的函数关系式；

（2）销售该商品第几天时，当天销售利润最大，最大利润是多少？

20．“全民防控新冠病毒”期间某公司推出一款消毒产品，成本价8元/千克，经过市场调查，该产品的日销售量y（千克）与销售单价x（元/千克）之间满足一次函数关系，该产品的日销售量与销售单价几组对应值如表：

（1）求y关于x的函数关系式（不要求写出x的取值范围）；

（2）设日销售利润为W，求出W与x的函数关系式；（注：日销售利润＝日销售量×（销售单价−成本单价）

（3）该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象，为了保证捐赠后每天的剩余利润不低于1500元，试确定该产品销售单价的范围．

21．某科技公司生产一款精密零件，每个零件的成本为80元，当每个零件售价为200元时，每月可以售出1000个该款零件，若每个零件售价每降低5元，每月可以多售出100个零件，设每个零件售价降低x元，每月的销售利润为w元．

（1）求w与x之间的函数关系式；

（2）为了更好地回馈社会，公司决定每销售1个零件就捐款n（0＜n≤6）元作为抗疫基金，当40≤x≤60时，捐款后每月最大的销售利润为135000元，求n的值．

22．我市某卖场的一专营柜台，专营一种电器，每台进价60元，调查发现，当销售价80元时，平均每月能售出1000台；当销售价每涨1元时，平均每月能少售出10台；该柜台每月还需要支出20000元的其它费用．为了防止不正当竞争，稳定市场，市物价局规定：“出售时不得低于80元/台，又不得高于180元/台”，设售价为x元/台时，月平均销售量为y台，月平均利润为w元．

（1）求y与x的函数关系式，w与x的函数关系式（写出x的取值范围）；

（2）每台售价多少元时，月销售利润最高，最高为多少元．

23．某文具店购进一批单价为12元的学习用品，按照相关部门规定其销售单价不低于进价，且不高于进价的1.5倍，通过分析销售情况，发现每天的销售量y（件）与销售单价x（元）满足一次函数关系，且当x＝15时，y＝50；当x＝17时，y＝30．

（1）求y与x之间的函数关系式；

（2）这种学习用品的销售单价定为多少时，每天可获得最大利润，最大利润是多少元？

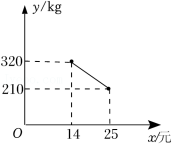
24．为扩大销售，某乡镇农贸公司在某平台新开了一家网店进行线上销售．在对一种特产（成本为10元/千克）在网店试销售期间发现每天销售量y（千克）与销售单价x（元）大致满足如图所示的函数关系（其中14≤x≤25）．

（1）写出y关于x的函数解析式，并求x＝20时，农贸公司每天销售该特产的利润；

（2）设农贸公司每天销售该特产的利润为W元，当销售单价x为多少元时，W最大？最大是多少元？

25．某公司把一种原料加工成产品进行销售，已知某月共加工原料x吨，恰好生产相同吨数的产品并能完全销售．每吨原料的加工成本Q（万元）与x（吨）满足关系式：Q＝ax+﹣30（其中a，b均为常数），且经过统计得到如下数据：

（1）求a、b的值；

（2）若该月的加工总成本为2052万元，求x的值；

（3）若生产的产品每吨售价为60万元，则该月可获得的最大利润是多少万元？

26．某商店销售一种商品，经市场调查发现：该商品的周销售量y（件）是出价x（元/件）的一次函数，其售价、周销售量、周销售利润w（元）的三组对应值如表：

注：周销售利润＝周销售量×（售价﹣进价）

（1）求y关于x的函数解析式（不要求写出自变量的取值范围）；

（2）当售价是多少元/件时，周销售利润最大，此时最大利润是多少元．

题型4：抛物线形问题

27．如图，正常水位时，抛物线形拱桥下的水面宽AB为20m，此时拱桥的最高点到水面的距离为4m．

（1）把拱桥看作一个二次函数的图象，建立恰当的平面直角坐标系，求出这个二次函数的表达式；

（2）当水面宽10m时，达到警戒水位，如果水位以0.2m/h的速度持续上涨，那么达到警戒水位后，再过多长时间此桥孔将被淹没？

28．2022北京冬奥会自由式滑雪空中技巧比赛中，某运动员比赛过程的空中剪影近似看作一条抛物线，跳台高度OA为4米，以起跳点正下方跳台底端O为原点，水平方向为横轴，竖直方向为纵轴，建立如图所示平面直角坐标系．已知抛物线最高点B的坐标为（4，12），着陆坡顶端C与落地点D的距离为2.5米，若斜坡CD的坡度i＝3：4（即＝）．

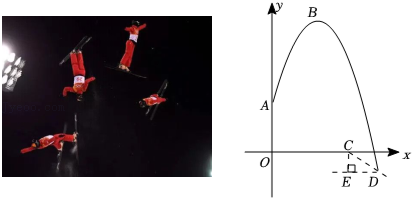
求：（1）点A的坐标；

（2）该抛物线的函数表达式；

（3）起跳点A与着陆坡顶端C之间的水平距离OC的长．（精确到0.1米）

（参考数据：≈1.73）

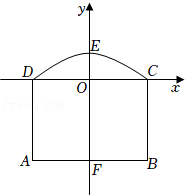
29．如图，隧道的截面由抛物线DEC和矩形ABCD构成，矩形的长AB为4m，宽BC为3m，以DC所在的直线为x轴，线段CD的中垂线为y轴，建立平面直角坐标系．y轴是抛物线的对称轴，最高点E到地面距离为4米．

（1）求出抛物线的解析式．

（2）在距离地面米高处，隧道的宽度是多少？

（3）如果该隧道内设单行道（只能朝一个方向行驶），现有一辆货运卡车高3.6米，宽2.4米，这辆货运卡车能否通过该隧道？通过计算说明你的结论．

30．某公园要修建一个圆形喷水池，在池中心竖直安装一根水管，水管OA长2.25m．在水管的顶端安装一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m．

（1）建立如图所示平面直角坐标系，求抛物线（第一象限部分）的解析式；

（2）不考虑其它因素，水池的直径至少要多少米才能使喷出的水流不落到池外？

（3）实际施工时，经测量，水池的最大半径只有2.5m，在不改变喷出的抛物线形水柱形状的情况下，且喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，需对水管的长度进行调整，求调整后水管的最大长度．

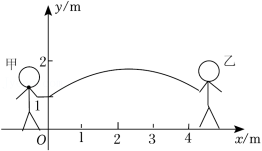
31．跳绳是大家喜爱的一项体育运动，当绳子甩到最高处时，其形状视为抛物线．如图是甲，乙两人将绳子甩到最高处时的示意图，已知两人拿绳子的手离地面的高度都为1m，并且相距4m，现以两人的站立点所在的直线为x轴，过甲拿绳子的手作x轴的垂线为y轴，建立如图所示的平面直角坐标系，且绳子所对应的抛物线解析式为．

（1）求绳子所对应的抛物线解析式（不要求写自变量的取值范围）；

（2）身高1.70m的小明，能否站在绳子的正下方，让绳子通过他的头顶？

（3）身高1.64m的小军，站在绳子的下方，设他距离甲拿绳子的手sm，为确保绳子能通过他的头顶，请求出s的取值范围．

32．如图①是气势如虹、古典凝重的开封北门，也叫安远门，有安定远方之寓意．其主门洞的截面如图②，上部分可看作是抛物线形，下部分可看作是矩形，边AB为16米，BC为6米，最高处点E到地面AB的距离为8米．

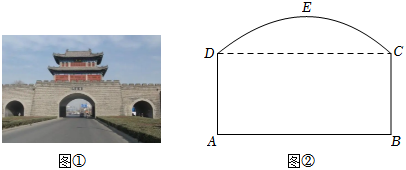
（1）请在图②中建立适当的平面直角坐标系，并求出抛物线的解析式．

（2）该主门洞内设双向行驶车道，正中间有0.6米宽的双黄线．车辆必须在双黄线两侧行驶，不能压双黄线，并保持车辆最高点与门洞有不少于0.6米的空隙（安全距离），试判断一辆大型货运汽车装载某大型设备后，宽3.7米，高6.6米，能否安全通过该主门洞？并说明理由．

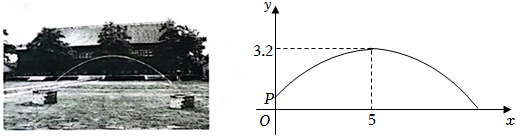
33．小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头P距地面0.7m，水柱在距喷水头P水平距离5m处达到最高，最高点距地面3.2m；建立如图所示的平面直角坐标系，并设抛物线的表达式为y＝a（x﹣h）2+k，其中x（m）是水柱距喷水头的水平距离，y（m）是水柱距地面的高度．

（1）求抛物线的表达式．

（2）爸爸站在水柱正下方，且距喷水头P水平距离3m．身高1.6m的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离．

34．如图是某抛物线形拱桥的截面图．某数学小组对这座拱桥很感兴趣，他们利用测量工具测出水面AB的宽为8米．设AB上的点E到点A的距离AE＝x米，点E到拱桥顶面的垂直距离EF＝y米．

通过取点、测量，数学小组的同学得到了x与y的几组值，如下表：

（1）拱桥顶面离水面AB的最大高度为 　 　米；

（2）请你帮助该数学小组建立平面直角坐标系，描出上表中各对对应值为坐标的点，并用平滑的曲线连接；

（3）测量后的某一天，由于降雨原因，水面比测量时上升1米．现有一游船（截面为矩形）宽度为4米，船顶到水面的高度为2米．要求游船从拱桥下面通过时，船顶到拱桥顶面的距离应大于0.5米．结合所画图象，请判断该游船是否能安全通过：　   　（填写“能”或“不能”）．

35．如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有二次函数关系．小明在一次击球过程中测得一些数据，如表所示．

根据相关信息解答下列问题．

（1）求小球的飞行高度h（单位：m）关于飞行时间t（单位：s）的二次函数关系式．

（2）小球从飞出到落地要用多少时间？

（3）小球的飞行高度能否达到20.5m？如果能，请求出相应的飞行时间；如果不能，请说明理由．