


苏科版七年级上册6.2 角优质学案设计
展开6.3 余角、补角、对顶角(1)
【学习目标】
基本目标:
1.在具体情境中了解余角、补角的概念,会求一个角的余角和补角;能根据已知条件判断两个角是否互余或者互补;
2.知道同角(等角)的余角相等、同角(等角)的补角相等,并且运用这些结论进行说理.
提高目标:经历探索同角(等角)的余角相等、同角(等角)的补角相等,学会有条理的思考和表达,提升推理能力.
【重点难点】
重点:余角、补角的概念和性质.
难点:余角与补角性质的灵活运用.
【预习导航】
一、读一读:阅读课本P155
二、想一想:
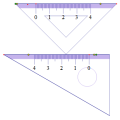
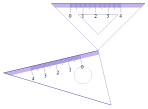
1.用一副三角尺摆出图1,∠α与∠β 的度数之间有怎样的关系?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
图①中∠α+∠β= ,图②中∠α+∠β= .
如果两个角的和是 ,这两个的角叫做 ,其中一个角是另一个角的 ;
如果两个角的和是 ,这两个的角叫做 ,其中一个角是另一个角的 .
2.(1)思考:同一块三角尺上有两个锐角互余吗?
(2)如果∠α+∠β=90°,那么∠α与∠β
反过来,如果∠α与∠β互余,那么
如果∠α+∠β=180°,那么∠α与∠β
反过来∠α与∠β互补,那么∠α+∠β=
3.已知3组角:



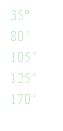

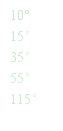
![]()
![]()
![]()
(1) 对A组中的每一个角,在B组中找出它的补角,并用线连接;
(2) B组中有哪些角的余角在C组中?分别找出这些角,并用线连接.
【课堂导学】
活动一:填表并回答问题.
∠α的度数 | 50° |
|
|
|
|
| n°(0<n<90) |
∠α的余角 |
| 45° |
|
|
|
|
|
∠α的补角 |
|
| 120° |
|
|
|
|
- ∠α取其他的一些度数,小组两人合作,一个人说出∠α 的度数,另一个人回答余角和补角的度数;
- 观察结果,你发现了什么?
- 同一个角的余角和补角有何关系?
活动二:已知一个角的补角是它的余角的3倍,那么这个角是多少度?你有几种方法解决?
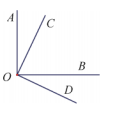 活动三:如图,∠AOB=∠COD=90°,
活动三:如图,∠AOB=∠COD=90°,
(1)若∠BOC=60°,则∠AOC与∠BOD有怎样的大小关系?为什么?
(2)若改变∠BOC的度数,则∠AOC与∠BOD有怎样的大小关系?为什么?
问题1:找出图中互余的角;
问题2:你能用推理的形式说明∠AOC与∠BOD相等的理由吗?
问题3:你能用一句话概括你发现的结论?
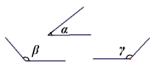
活动四:如果∠α与∠β互为补角,∠α与∠γ互补,那么∠β与∠γ相等吗?为什么?
【课堂检测】
1.判断:
(1)90°的角叫余角,180°的角叫补角. ( )
(2)如果∠1+∠2+∠3=180°,那么∠1、∠2与∠3互补. ( )
(3)如果两个角相等,则它们的补角相等. ( )
(4)如果∠α>∠β,那么∠α的补角比∠β的补角大. ( )
(5)一个锐角的余角一定小于这个角的补角. ( )
(6)一个角的补角一定比这个角小 ( )
2.∠α=30°27′,则它的余角等于 ;∠β的补角是106°8′32″,
则∠β= .
![]()
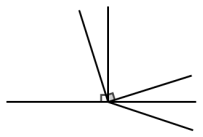
![]() 3.如图,O是直线AB上的一点,∠AOE=∠FOD=90°,OB平分∠COD,则图中与∠DOE互余的角有哪些?与∠DOE互补的角有哪些?
3.如图,O是直线AB上的一点,∠AOE=∠FOD=90°,OB平分∠COD,则图中与∠DOE互余的角有哪些?与∠DOE互补的角有哪些?
![]()
![]()
![]()
![]()
![]()
4.如图,∠A+∠B=900, ∠BCD+∠B=900. ∠A与∠BCD有怎样的大小关系?为什么?

![]()
![]()
![]()
![]()
5.已知∠α与∠β互为补角, 且∠β比∠α大30°.求∠α 、∠β的度数.
![]()
![]()
![]() 6.如图,直线AB、CD相交于点O,∠AOE=∠COF=90°.∠AOF与∠DOE、∠BOF与∠COE又怎样的大小关系?为什么?
6.如图,直线AB、CD相交于点O,∠AOE=∠COF=90°.∠AOF与∠DOE、∠BOF与∠COE又怎样的大小关系?为什么?
![]()
![]()
![]()
![]()
【课后巩固】
一、基础检测
- (1)∵∠1和∠2互余, (2)∵∠1和∠2互补,
∴∠1+∠2= ∴∠1+∠2=
(或∠1= -∠2). (或∠1= -∠2).
2.已知∠α=50°17′,则它的余角等于 ;∠β的补角是102°38′,则∠β= .
3.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3= .
4.∠1与∠2互余,∠1=(6x+8)°,∠2=(4x-8)°,则∠1= ,∠2= .
5.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ= .
6.若互为补角的两个角的度数之比为3:2,则这个两个角的度数分别为 和 .
7.如图,∠AOC和∠BOD都是直角,如果∠AOB=140°,那么∠DOC= .
 8.若∠1与∠2互为补角,且∠1<∠2,则∠1的余角为 ( )
8.若∠1与∠2互为补角,且∠1<∠2,则∠1的余角为 ( )
A.∠1 B.∠1+∠2 C.![]() (∠1+∠2 ) D.
(∠1+∠2 ) D.![]() (∠2-∠1)
(∠2-∠1)
9.(1)一个角比它的余角大25°,求这个角的度数;
(2)一个角的余角是这个角的补角的![]() ,求这个角的度数.
,求这个角的度数.
拓展延伸
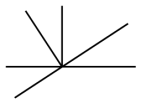
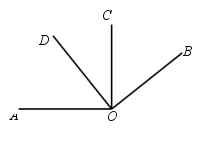
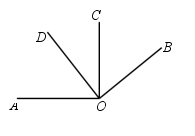
10.(1)如图1,∠AOB、∠COD都是直角,试猜想∠AOD与∠BOC在数量上存在
![]() 相等、互余还是互补的关系,并说明你的理由;
相等、互余还是互补的关系,并说明你的理由;
![]()
![]()
![]()
![]()
图1 图2
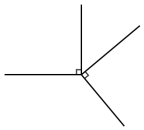
(3)若∠COD绕着点O不停地旋转,则(1)中的猜想 成立(填“仍旧”或“不一定”).
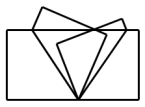
11.小明想用一张长方形纸折成一个纸袋,折法如图所示,两条折痕的夹角70°(即∠POQ=70°),将折过来的重叠部分抹上胶水,即可做成一个纸袋,那么粘胶水的部分所构成的∠A′OB′= °.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
数学苏科版6.5 垂直优秀导学案及答案: 这是一份数学苏科版6.5 垂直优秀导学案及答案,文件包含65垂直1导学案无答案doc、65垂直2导学案无答案doc等2份学案配套教学资源,其中学案共8页, 欢迎下载使用。
初中数学苏科版七年级上册6.2 角优秀学案: 这是一份初中数学苏科版七年级上册6.2 角优秀学案,文件包含62角1导学案无答案doc、62角2导学案无答案doc等2份学案配套教学资源,其中学案共8页, 欢迎下载使用。
初中数学苏科版七年级上册6.3 余角 补角 对顶角学案: 这是一份初中数学苏科版七年级上册6.3 余角 补角 对顶角学案,共12页。学案主要包含了学习目标,重点难点,导学指导等内容,欢迎下载使用。













