


所属成套资源:【单元检测】沪教版(五四学制)初中数学 八年级上册 单元测试卷
初中数学沪教版 (五四制)八年级上册18.2 正比例函数优秀单元测试课后复习题
展开
这是一份初中数学沪教版 (五四制)八年级上册18.2 正比例函数优秀单元测试课后复习题,共11页。试卷主要包含了函数y=自变量x的取值范围是等内容,欢迎下载使用。
2021-2022学年沪教新版八年级上册数学《第18章 正比例函数与反比例函数》单元测试卷一.选择题1.在圆的周长C=2πR中,常量与变量分别是( )A.2是常量,C、π、R是变量 B.2π是常量,C、R是变量 C.C、2是常量,R是变量 D.2是常量,C、R是变量2.在圆的面积计算公式S=πR2中,变量是( )A.S B.R C.π,R D.S,R3.甲以每小时20km的速度行驶时,他所走的路程s(km)与时间t(h)之间可用公式s=20t来表示,则下列说法正确的是( )A.数20和s,t都是变量 B.s是常量,数20和t是变量 C.数20是常量,s和t是变量 D.t是常量,数20和s是变量4.矩形ABCD的边BC在直线l上,AB=2,BC=4,P是AD边上一动点且不与点D重合,连接CP,过点P作∠APE=∠CPD,交直线l于点E,若PD的长为x,△PEC与矩形ABCD重合部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) A.
A. B.
B.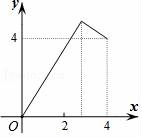 C.
C.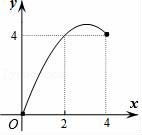 D.
D. 5.函数y=
5.函数y=![]() 自变量x的取值范围是( )A.x≥﹣1 B.x≠2 C.x≥﹣1且x≠2 D.﹣1≤x<26.小亮在放学回家的路上,看到同学小明在前方,便加快速度追赶小明,在距离学校60米处追上了小明,如图反映了这一过程,其中s(单位:米)表示与学校的距离,t(单位:秒)表示时间.根据相关信息,以下说法错误的是( )
自变量x的取值范围是( )A.x≥﹣1 B.x≠2 C.x≥﹣1且x≠2 D.﹣1≤x<26.小亮在放学回家的路上,看到同学小明在前方,便加快速度追赶小明,在距离学校60米处追上了小明,如图反映了这一过程,其中s(单位:米)表示与学校的距离,t(单位:秒)表示时间.根据相关信息,以下说法错误的是( ) A.开始时小明与小亮之间的距离是30米 B.15秒时小亮追上了小明 C.小亮走了60米追上小明 D.小亮追上小明时,小明走了60米7.圆的面积公式为S=πr2,其中变量是( )A.S B.π C.r D.S和r8.下列图象中,表示y是x的函数的是( )A.
A.开始时小明与小亮之间的距离是30米 B.15秒时小亮追上了小明 C.小亮走了60米追上小明 D.小亮追上小明时,小明走了60米7.圆的面积公式为S=πr2,其中变量是( )A.S B.π C.r D.S和r8.下列图象中,表示y是x的函数的是( )A.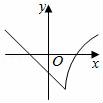 B.
B.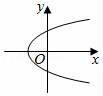 C.
C.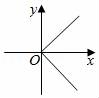 D.
D.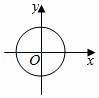 9.根据如图所示的计算程序,若输入的值x=﹣3,则输出y的值为( )
9.根据如图所示的计算程序,若输入的值x=﹣3,则输出y的值为( )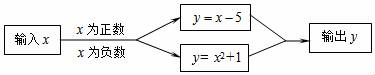 A.﹣2 B.﹣8 C.10 D.1310.如果每盒笔售价16元,共有10支,用y(元)表示笔的售价,x表示笔的支数,那么y与x的关系式为( )A.y=10x B.y=16x C.y=
A.﹣2 B.﹣8 C.10 D.1310.如果每盒笔售价16元,共有10支,用y(元)表示笔的售价,x表示笔的支数,那么y与x的关系式为( )A.y=10x B.y=16x C.y=![]() x D.y=
x D.y=![]() x二.填空题11.自变量x与因变量y的关系如图,当x每增加1时,y增加 .
x二.填空题11.自变量x与因变量y的关系如图,当x每增加1时,y增加 . 12.若某地打长途电话3分钟之内收费1.8元,每增加1分钟加收0.5元,当通话时间为t分钟时(t≥3且t为整数),电话费y(元)与通话时间t(分)之间的关系式为 .13.在函数y=
12.若某地打长途电话3分钟之内收费1.8元,每增加1分钟加收0.5元,当通话时间为t分钟时(t≥3且t为整数),电话费y(元)与通话时间t(分)之间的关系式为 .13.在函数y=![]() 中,自变量x的取值范围是 .14.已知f(x)=
中,自变量x的取值范围是 .14.已知f(x)=![]() ,那么f(3)的值是 .15.林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中 是常量, 是变量.16.在圆的周长公式C=2πr中,变量是 , ,常量是 .17.圆的面积S与半径R之间的关系式是S=πR2,其中自变量是 .18.端午期间,王老师一家自驾游去了离家170km的某地,如图是他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象,当他们离目的地还有20km时,汽车一共行驶的时间是 .
,那么f(3)的值是 .15.林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中 是常量, 是变量.16.在圆的周长公式C=2πr中,变量是 , ,常量是 .17.圆的面积S与半径R之间的关系式是S=πR2,其中自变量是 .18.端午期间,王老师一家自驾游去了离家170km的某地,如图是他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象,当他们离目的地还有20km时,汽车一共行驶的时间是 .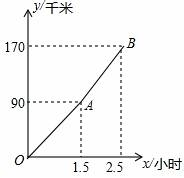 19.(多选)下列图象中,表示y是x的函数的有 .
19.(多选)下列图象中,表示y是x的函数的有 .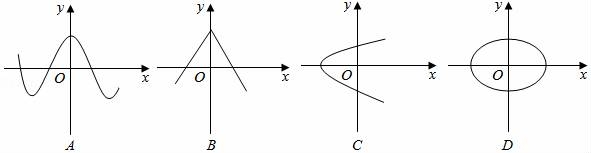 20.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是 .
20.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是 .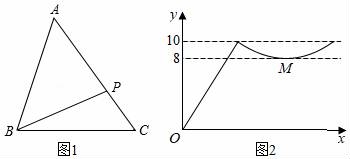 三.解答题21.如图是一位病人的体温记录图,看图回答下列问题:
三.解答题21.如图是一位病人的体温记录图,看图回答下列问题: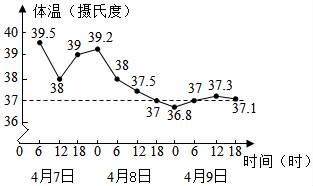 (1)自变量是 ,因变量是 ;(2)护士每隔 小时给病人量一次体温;(3)这位病人的最高体温是 摄氏度,最低体温是 摄氏度;(4)他在4月8日12时的体温是 摄氏度;(5)图中的横虚线表示 ;22.求函数y=
(1)自变量是 ,因变量是 ;(2)护士每隔 小时给病人量一次体温;(3)这位病人的最高体温是 摄氏度,最低体温是 摄氏度;(4)他在4月8日12时的体温是 摄氏度;(5)图中的横虚线表示 ;22.求函数y=![]() 的自变量x的取值范围.23.写出下列各问题中的关系式中的常量与变量:(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.24.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.25.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:x…123579…y…1.983.952.631.581.130.88…小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小腾的探究过程,请补充完整:(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(2)根据画出的函数图象,写出:①x=4对应的函数值y约为 ;②该函数的一条性质: .
的自变量x的取值范围.23.写出下列各问题中的关系式中的常量与变量:(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.24.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.25.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:x…123579…y…1.983.952.631.581.130.88…小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小腾的探究过程,请补充完整:(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(2)根据画出的函数图象,写出:①x=4对应的函数值y约为 ;②该函数的一条性质: . 26.如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.(1)在这个变化过程中,自变量、因变量各是什么?(2)如果小正方形的边长为xcm,图中阴影部分的面积为ycm2,请写出y与x的关系式;(3)当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?
26.如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.(1)在这个变化过程中,自变量、因变量各是什么?(2)如果小正方形的边长为xcm,图中阴影部分的面积为ycm2,请写出y与x的关系式;(3)当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?
参考答案与试题解析一.选择题1.解:∵在圆的周长公式C=2πR中,C与R是改变的,π是不变的;∴变量是C,R,常量是2π.故选:B.2.解:在圆的面积计算公式S=πR2中,变量为S,R.故选:D.3.解:在s=20t中,数20是常量,s和t是变量,故选:C.4.解:当x≤2时,y=2x,是一次函数;当2<x≤4时,y=2x﹣![]() =﹣2x+16﹣
=﹣2x+16﹣![]() ,是一次函数与反比例函数的叠加函数.只有A符合条件.故选:A.5.解:由题意得,x+1≥0,x﹣2≠0,解得,x≥﹣1且x≠2,故选:C.6.解:A、由纵坐标看出,一开始时小明与小亮之间的距离是30米,故A不合题意;B、由横坐标看出,15秒时小亮追上了小明,故B不合题意;C、由纵坐标看出,小亮走了60米追上小明,故C不合题意;D、由纵坐标看出,小亮追上小明时,小明走了30米,故D符合题意.故选:D.7.解:S=πr2中,S是圆的面积,r是圆的半径,S随r的变化而变化,∴π是常量,S和r是变量.故选:D.8.解:根据函数的定义可知,每给定自变量x一个值,都有唯一的函数值y与之相对应,所以B、C、D不合题意.故选:A.9.解:当x=﹣3时,由程序图可知:y=x2+1=(﹣3)2+1=9+1=10,故选:C.10.解:由题意得,y=
,是一次函数与反比例函数的叠加函数.只有A符合条件.故选:A.5.解:由题意得,x+1≥0,x﹣2≠0,解得,x≥﹣1且x≠2,故选:C.6.解:A、由纵坐标看出,一开始时小明与小亮之间的距离是30米,故A不合题意;B、由横坐标看出,15秒时小亮追上了小明,故B不合题意;C、由纵坐标看出,小亮走了60米追上小明,故C不合题意;D、由纵坐标看出,小亮追上小明时,小明走了30米,故D符合题意.故选:D.7.解:S=πr2中,S是圆的面积,r是圆的半径,S随r的变化而变化,∴π是常量,S和r是变量.故选:D.8.解:根据函数的定义可知,每给定自变量x一个值,都有唯一的函数值y与之相对应,所以B、C、D不合题意.故选:A.9.解:当x=﹣3时,由程序图可知:y=x2+1=(﹣3)2+1=9+1=10,故选:C.10.解:由题意得,y=![]() x=
x=![]() x,故选:C.二.填空题11.解:当x增加1变为x+1,则y变为y1=2(x+1)+10=2x+2+10=2x+12,∴y1﹣y=2x+12﹣(2x+10)=2x+12﹣2x﹣10=2,故答案为:2.12.解:由题意得,y=1.8+0.5(t﹣3)=0.5t+0.3,故答案为:y=0.5t+0.3.13.解:当x﹣2≠0,即x≠2时,函数y=
x,故选:C.二.填空题11.解:当x增加1变为x+1,则y变为y1=2(x+1)+10=2x+2+10=2x+12,∴y1﹣y=2x+12﹣(2x+10)=2x+12﹣2x﹣10=2,故答案为:2.12.解:由题意得,y=1.8+0.5(t﹣3)=0.5t+0.3,故答案为:y=0.5t+0.3.13.解:当x﹣2≠0,即x≠2时,函数y=![]() 有意义.故答案为:全x≠2.14.解:∵f(x)=
有意义.故答案为:全x≠2.14.解:∵f(x)=![]() ,∴f(3)=
,∴f(3)=![]() =1,故答案为:1.15.解:在这三个量当中元/升是常量,数量、金额是变量.16.解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;∴变量是C,r,常量是2π.17.解:根据函数的定义:对于函数中的每个值R,变量S按照一定的法则有一个确定的值S与之对应可知R是自变量,π是常量.故答案为:R.18.解:设AB段的函数解析式是y=kx+b,y=kx+b的图象过A(1.5,90),B(2.5,170),
=1,故答案为:1.15.解:在这三个量当中元/升是常量,数量、金额是变量.16.解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;∴变量是C,r,常量是2π.17.解:根据函数的定义:对于函数中的每个值R,变量S按照一定的法则有一个确定的值S与之对应可知R是自变量,π是常量.故答案为:R.18.解:设AB段的函数解析式是y=kx+b,y=kx+b的图象过A(1.5,90),B(2.5,170),![]() ,解得
,解得![]() ,∴AB段函数的解析式是y=80x﹣30,离目的地还有20千米时,即y=170﹣20=150km,当y=150时,80x﹣30=150解得:x=2.25h,故答案为:2.25h19.解:A、能表示y是x的函数,故此选项合题意;B、能表示y是x的函数,故此选项不合题意;C、不能表示y是x的函数,故此选项不合题意;D、不能表示y是x的函数,故此选项不符合题意;故答案为:A、B.20.解:根据图象可知点P在BC上运动时,此时BP不断增大,由图象可知:点P从B向C运动时,BP的最大值为10,即BC=10,由于M是曲线部分的最低点,∴此时BP最小,即BP⊥AC,BP=8,∴由勾股定理可知:PC=6,由于图象的曲线部分是轴对称图形,∵图象右端点函数值为10,∴AB=BC=10,∴PA=PC=6(三线合一),∴AC=12,∴△ABC的面积为:
,∴AB段函数的解析式是y=80x﹣30,离目的地还有20千米时,即y=170﹣20=150km,当y=150时,80x﹣30=150解得:x=2.25h,故答案为:2.25h19.解:A、能表示y是x的函数,故此选项合题意;B、能表示y是x的函数,故此选项不合题意;C、不能表示y是x的函数,故此选项不合题意;D、不能表示y是x的函数,故此选项不符合题意;故答案为:A、B.20.解:根据图象可知点P在BC上运动时,此时BP不断增大,由图象可知:点P从B向C运动时,BP的最大值为10,即BC=10,由于M是曲线部分的最低点,∴此时BP最小,即BP⊥AC,BP=8,∴由勾股定理可知:PC=6,由于图象的曲线部分是轴对称图形,∵图象右端点函数值为10,∴AB=BC=10,∴PA=PC=6(三线合一),∴AC=12,∴△ABC的面积为:![]() ×12×8=48,故答案为:48.三.解答题21.解:(1)自变量是时间,因变量是体温;(2)护士每隔6小时给病人量一次体温;(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;(4)他在4月8日12时的体温是37.5摄氏度;(5)图中的横虚线表示人的正常体温;故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.22.解:根据二次根式的意义,被开方数4+2x≥0,解得x≥﹣2;根据分式有意义的条件,x﹣1≠0,解得x≠1,因为x≥﹣2的数中包含1这个数,所以自变量的范围是x≥﹣2且x≠1.23.解:(1)常量:6;变量:n,t.(2)常量:40;变量:s,t.24.解:由题意得:y=2x,常量是2,变量是x、y,x是自变量,y是x的函数.25.解:(1)如图,
×12×8=48,故答案为:48.三.解答题21.解:(1)自变量是时间,因变量是体温;(2)护士每隔6小时给病人量一次体温;(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;(4)他在4月8日12时的体温是37.5摄氏度;(5)图中的横虚线表示人的正常体温;故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.22.解:根据二次根式的意义,被开方数4+2x≥0,解得x≥﹣2;根据分式有意义的条件,x﹣1≠0,解得x≠1,因为x≥﹣2的数中包含1这个数,所以自变量的范围是x≥﹣2且x≠1.23.解:(1)常量:6;变量:n,t.(2)常量:40;变量:s,t.24.解:由题意得:y=2x,常量是2,变量是x、y,x是自变量,y是x的函数.25.解:(1)如图, (2)①x=4对应的函数值y约为2.0;②该函数有最大值.故答案为2,该函数有最大值.26.解:(1)∵当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化,∴小正方形的边长是自变量,阴影部分的面积为因变量;(2)由题意可得:y=122﹣4x2=144﹣4x2.(3)由(2)知:y=144﹣4x2,当小正方形的边长由1cm变化到5cm时,x增大,x2也随之增大,﹣4x2则随着x的增大而减小,所以y随着x的增大而减小,当x=1cm时,y有最大值,
(2)①x=4对应的函数值y约为2.0;②该函数有最大值.故答案为2,该函数有最大值.26.解:(1)∵当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化,∴小正方形的边长是自变量,阴影部分的面积为因变量;(2)由题意可得:y=122﹣4x2=144﹣4x2.(3)由(2)知:y=144﹣4x2,当小正方形的边长由1cm变化到5cm时,x增大,x2也随之增大,﹣4x2则随着x的增大而减小,所以y随着x的增大而减小,当x=1cm时,y有最大值,![]() =140(cm2).当x=5cm时,y有最小值,y最小=144﹣4×52=44(cm2).∴当小正方形的边长由1cm变化到5cm时,阴影部分的面积由140cm2变到44cm2
=140(cm2).当x=5cm时,y有最小值,y最小=144﹣4×52=44(cm2).∴当小正方形的边长由1cm变化到5cm时,阴影部分的面积由140cm2变到44cm2
相关试卷
这是一份初中数学沪教版 (五四制)八年级上册18.3 反比例函数精品课后复习题,共6页。试卷主要包含了单选题,三象限D.第二,解答题等内容,欢迎下载使用。
这是一份数学八年级上册18.2 正比例函数精品习题,共7页。试卷主要包含了单选题,四象限,解答题等内容,欢迎下载使用。
这是一份初中数学沪教版 (五四制)八年级上册16.1 二次根式优秀单元测试同步练习题,共7页。试卷主要包含了下列式子书写正确的有,下列代数式书写正确的是,下列代数式的书写格式规范的是,下列代数式中,不是整式的是等内容,欢迎下载使用。










