【阶段测试】人教版数学九年级上册--第二十五章 概率初步 达标测试卷（含答案）

第二十五章  概率初步　 达标测试卷

（时间：120分钟  分数：120分）

一、选择题(共10道题,每小题3分,共30分)

1.下列事件是必然事件的是(　  　)

A.三角形内角和是180° 

B.端午节赛龙舟,红队获得冠军

C.掷一枚均匀骰子,点数是6的一面朝上

D.打开电视,正在播放神舟十四号载人飞船发射实况

2.从一副扑克牌中任意抽取1张,下列事件发生的可能性最大的是(　  　)

A.这张牌是“A”  B.这张牌是“大王”

C.这张牌是“黑桃” D.这张牌的点数是10

3.下列说法错误的是(　  　)

A.必然事件发生的概率是1

B.通过大量重复试验,可以用频率估计概率

C.概率很小的事件不可能发生

D.投一枚图钉,“钉尖朝上”的概率不能用列举法求得

4.“彩缕碧筠粽,香粳白玉团.”端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是(　  　)

A. B. C. D.

5.一个不透明的袋子里装有颜色不同的16个红球和若干个白球,每次从袋子里摸出来一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,估计袋中白球有(　  　)

A.40个 B.38个 C.26个 D.24个

6.定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“967”就是一个“V数”.若十位上的数字为4,则从3,5,7,9中任选两数,能与4组成“V数”的概率是(　  　)

A.  B.　  C.　 D.

7.甲、乙两人各自掷一个普通的正方体骰子,如果两者之积为偶数,那么甲得1分;如果两者之积为奇数,那么乙得1分,此游戏(　  　)

A.对甲有利 B.对乙有利 C.是公平的 D.以上都不对

8.小明用大小和形状都完全一样的正方体按照一定规律摆放了一组图案(如图),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第①个图案中有1个正方体,第②个图案中有3个正方体,第③个图案中有6个正方体……按照此规律,从第个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是(　  　)

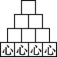
                  ①   ②     ③      ④

　……

A. B. C. D.

9.现有A,B,C三个不透明的盒子,A盒中装有红、黄、蓝球各1个,B盒中装有红、黄球各1个,C盒中装有红、蓝球各1个,这些球除颜色外都相同.现分别从A,B,C三个盒子中任意摸出1个球,摸出的3个球至少有1个红球的概率是(　  　)

A.　 B.　　 C.　 D.

10.用图中两个可自由转动的转盘A,B做“配紫色”游戏:分别旋转两个转盘A,B,如果其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是(　  　)

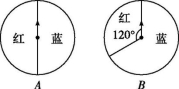
A.   B.   C.   D.

二、填空题(共6道题,每小题3分,共18分)

11.有下列四个事件:①向空中抛一块小石子,小石子会飞向太空;②圆心角大于圆周角;③三点确定一个圆;④大海捞针.其中是随机事件的是　       　.(填序号) 

12.某校篮球队进行篮球训练,下表是某队员投篮的统计结果,根据表格可知该队员一次投篮命中的概率大约是　    　.(精确到0.01) 

13.一只蚂蚁在如图的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中一条路径,则它遇到食物的概率是　   　. 

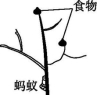
第13题图

14.如图是由12个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是　    　. 

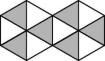
第14题图

15.如图,麻将是中国的国粹之一,是中国古人发明的一种博弈游戏,玩法最为复杂有趣.它开局拿牌要投两枚骰子,将两枚骰子的点数相加之和除以4看余数来决定是在哪家开始拿牌.余数为1则在自家拿牌,余数为2则在下家拿牌,余数为3则在对家拿牌,能被4整除就在上家拿牌,则在自家拿牌的概率为　          . 

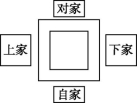
第15题图

16.如图,随机地闭合开关S1,S2,S3,S4,S5中的三个,能够使灯泡L1,L2同时发光的概率是　         . 

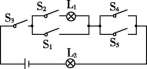
第16题图

三、解答题(共6道题,共52分)

17.(8分)某运动员进行打靶训练,对该名运动员打靶正中靶心的情况进行统计,并绘制成了如图的统计图,请根据图中信息回答问题:

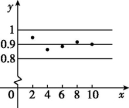
(1)该名运动员正中靶心的频率在　　　　附近摆动,他正中靶心的概率估计值为　　　　. 

(2)如果一次练习时他一共打了150枪.

①试估计他正中靶心的枪数.

②如果他想要在这次练习中打中靶心180枪,请计算出他还需要打大约多少枪.

18.(8分)一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球个数比白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是.

(1)求袋中红球的个数;

(2)求从袋中摸出一个球是白球的概率;

(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.

19.(8分)一个不透明的口袋中装有4张卡片,卡片上分别标有数字1,-2,3,-4,这些卡片除数字外都相同.小兴从口袋中随机抽取一张卡片,小华从剩余的三张卡片中随机抽取一张.

(1)请你用画树状图或列表的方法,列出两人抽到的数字之积所有可能的结果;

(2)求两人抽到的数字之积为正数的概率.

20.(8分)两千多年前我们的祖先就使用“算筹”表示数,后渐渐发展为算盘.算筹有纵式和横式两种排列方式,0～9各个数字及其算筹表示的对应关系如表所示.

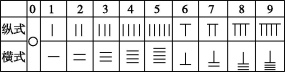
排列数字时,个位采用纵式,十位采用横式,百位采用纵式,千位采用横式……纵式和横式依次交替出现.如“”表示87,“”表示502.在“”“”“”“”“”按照一定顺序排列成的三位数中任取一个,求取到奇数的概率.

21.(9分)有甲、乙两个不透明的布袋,甲袋中装有3个形状、大小完全相同的小球,分别标有数字0,1,2;乙袋中装有3个形状、大小完全相同的小球,分别标有数字-1,-2,0.现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M的坐标为(x,y).

(1)用画树状图或列表的方法列举点M所有可能的坐标;

(2)求点M(x,y)在函数y=-x+1的图象上的概率;

(3)在平面直角坐标系xOy中,☉O的半径是2,求过点M(x,y)能作☉O的切线的概率.

22.(11分)中华文化源远流长,文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成尚不完整的统计图,如图.

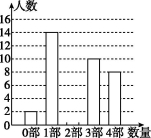
①

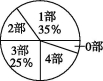
②

请根据以上信息,解答下列问题:

(1)求本次调查所得数据的众数和中位数;

(2)求扇形统计图中“4部”所在扇形的圆心角度数;

(3)请将条形统计图补充完整;

(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,请用列表或画树状图的方法求他们恰好选中同一名著的概率.

第二十五章　达标测试卷

一、选择题

1.A　2.C　3.C　4.D　5.D　6.D　7.A　8.D

9.B　解析:画树状图如图所示.

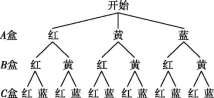
共有12种等可能的结果,摸出的3个球至少有1个红球的结果有    10种,

∴摸出的3个球至少有1个红球的概率为=.

故选B.

10.D　解析:如图,将B转盘中的蓝色部分等分成两部分.

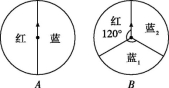
画树状图如图所示.

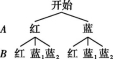
∴P(配成紫色)==.故选D.

二、填空题

11.②③④　12.0.72　13.　14.

15.　解析:列表如下:

共有36种等可能的结果,其中两枚骰子的点数相加之和除以4的余数为1的结果有(1,4),(2,3),(3,2),(3,6),(4,1),(4,5),(5,4), (6,3),共8种,

∴在自家拿牌的概率为=.

16.　解析:从五个开关中随机地闭合三个,可能是(S1,S2,S3), (S1,S2,S4),(S1,S2,S5),(S1,S3,S4),(S1,S3,S5),(S1,S4,S5),(S2,S3,S4), (S2,S3,S5),(S2,S4,S5),(S3,S4,S5),共10种可能,其中(S2,S3,S4), (S2,S3,S5)能够使两个灯泡L1,L2同时发光,∴其概率为=.

三、解答题

17.解:(1)0.9　0.9

(2)①150×0.9=135(枪),

∴估计他正中靶心的枪数为135枪.

②180÷0.9=200(枪),∴200-150=50(枪),

∴他还需要打大约50枪.

18.解:(1)100×=30(个),∴袋中红球的个数为30.

(2)设白球有x个,则黄球有(2x-5)个.根据题意,得x+(2x-5)+30=100,解得x=25,

∴从袋中摸出一个球是白球的概率为=.

(3)取走10个非红色的球,则剩余90个球,其中红球有30个,

则从剩余的球中摸出一个球是红球的概率为=.

19.解:(1)画树状图如图所示.

(2)由(1)可知共有12种可能性,其中两人抽到的数字之积为正数的可能性有4种,

∴两人抽到的数字之积为正数的概率是=.

20.解:“”“”“”“”“”表示的数字分别为0,2(横式),3(纵式),6(纵式),9(横式),按照一定顺序排成的三位数中,百位数字只可在3或6中任选一个,

①若百位数字为3,则三位数有306,320,326,390,396;

②若百位数字为6,则三位数有603,620,623,690,693;

共有10种等可能性结果,其中满足条件的三位数有603,623,693,

共3个,

∴取到奇数的概率P=.

21.解:(1)画树状图如图所示.

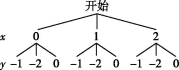
由树状图知共有9种等可能的结果,

它们分别是(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1), (2,-2),(2,0).

(2)∵在函数y=-x+1的图象上的点有(1,0),(2,-1),

∴点M(x,y)在函数y=-x+1的图象上的概率=.

(3)∵在☉O上的点有(0,-2),(2,0),在☉O外的点有(1,-2),(2,-1), (2,-2),

∴过点M(x,y)能作☉O的切线的点有5个,

∴过点M(x,y)能作☉O的切线的概率=.

22.解:(1)本次调查的人数为10÷25%=40,

∴读完2部的学生有40-2-14-10-8=6(人),

∴本次调查所得数据的众数是1部,中位数是(2+2)÷2=2(部).

(2)扇形统计图中“4部”所在扇形的圆心角为360°×=72°.

(3)由(1)知读完2部的学生有6人,

补充完整条形统计图如图①所示.

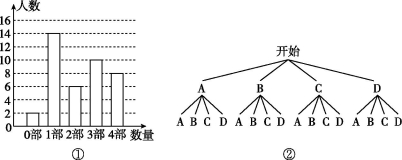
(4)《西游记》《三国演义》《水浒传》《红楼梦》分别用字母A,B,C,D表示,画树状图如图②,

∴共有16种等可能的结果,

其中他们恰好选中同一名著的结果有4种,

∴他们恰好选中同一名著的概率是=.