【阶段测试】人教版数学九年级上册--第二十四章 圆 达标测试卷（含答案）

第二十四章  圆　 达标测试卷

（时间：120分钟  分数：120分）

一、选择题(共10道题,每小题3分,共30分)

1.有下列说法:①等弧所对的圆周角相等;②过三点可以作一个圆;③平分弦的直径垂直于弦;④半圆是一条弧.其中正确的说法是(　  　)

A.①②③④ B.①②③ C.②③④ D.①④

2.如图,E,F,G为圆上的三点,∠FEG=50°,点P可能是圆心的是(　  　)

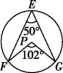
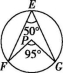
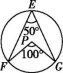
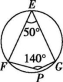
                  A      B       C      D

3.若☉O的半径为6,一条弦长6,则以3为半径的同心圆与这条弦的关系是(　  　)

A.相切 B.相交  C.相离 D.相切或相交

4.如图,AB是☉O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于(　  　)

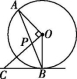
第4题图

A.75° B.70° C.65° D.60°

5.如图,点A,B,C,D在☉O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC等于(　  　)

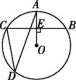
第5题图

A.2 B.4  C.   D.2

6.如图,PA,PB切☉O于点A,B,直线FG切☉O于点E,交PA于点F,交PB于点G,若PA=8 cm,则△PFG的周长是(　  　)

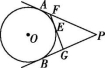
第6题图

A.8 cm B.12 cm C.16 cm D.20 cm

7.蒙古包可以近似地看作由圆锥和圆柱组成.如图是一个蒙古包的示意图,底面圆半径DE=2 m,圆锥的高AC=1.5 m,圆柱的高CD=2.5 m,则下列说法错误的是(　  　)

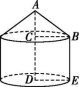
第7题图

A.圆柱的底面积为4π m2  B.圆柱的侧面积为10π m2

C.圆锥的母线AB长为2.25 m D.圆锥的侧面积为5π m2

8.如图,四边形ABCD内接于☉O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为(　  　)

A.56° B.62° C.68° D.78°

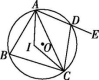
第8题图

9.如图,设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h,r,R,则下列结论不正确的是(　  　)

第9题图

A.h=R+r  B.R=2r  C.r=a  D.R=a

10.如图,☉O是等边三角形ABC的外接圆,点D是弧AC上一动点(不与点A,C重合),下列结论:①∠ADB=∠BDC;②DA=DC;③当DB最长时,DB=2DC;④DA+DC=DB.其中一定正确的结论有(　  　)

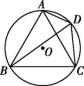
第10题图

A.1个 B.2个 C.3个 D.4个

二、填空题(共6道题,每小题3分,共18分)

11.如图,△ABC内接于☉O,AB是直径,过点A作☉O的切线AD.若∠B=35°,则∠DAC的度数是　     　度. 

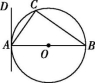
第11题图

12.在四边形ABCD中,∠A=∠C=90°,☉O是△ABD的外接圆,若AB=6,AD=8,则OC=　      　. 

13.如图,小区内有个圆形花坛O,点C在弦AB上,AC=11, BC=21,OC=13,则这个花坛的面积为　      　.(结果保留π) 

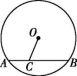
第13题图

14.如图,☉O与正六边形OABCDE的边OA,OE分别交于点F,G,M是劣弧FG的中点.若FM=2,则☉O的半径为　        　. 

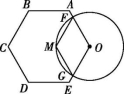
第14题图

15.如图,☉O的直径CD为6 cm,OA,OB都是☉O的半径,∠AOD=

2∠AOB=60°,点P在直径CD上移动,则AP+BP的最小值为　   　cm.

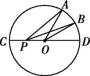
第15题图

16.如图,分别以边长为2的等边三角形ABC的三个顶点为圆心,以边长为半径作弧,三段弧所围成的图形是一个曲边三角形,已知☉O是

△ABC的内切圆,则阴影部分的面积为　          . 

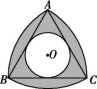
第16题图

三、解答题(共6道题,共52分)

17.(7分)如图,△ABC内接于☉O,AD∥BC交☉O于点D,DF∥AB交BC于点E,交☉O于点F,连接AF,CF.

(1)求证:AC=AF;

(2)若☉O的半径为3,∠CAF=30°,求的长(结果保留π).

18.(8分)如图,在平面直角坐标系中,有一圆弧经过三个点A,B,C,且点A,B,C的坐标分别为A(0,4),B(-4,4),C(-6,2).

(1)该圆弧所在圆的圆心M的坐标为　　　　　　; 

(2)☉M的半径为　　　　　　; 

(3)点D(-5,-2)在☉M　　　　　　;(填“内”“外”或“上”) 

(4)求点O到☉M上最近的点的距离.

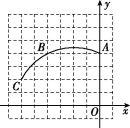
题图

19.(8分)如图,圆O中两条互相垂直的弦AB,CD交于点E.

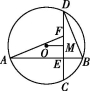
(1)若M是CD的中点,OM=3,CD=12,求圆O的半径长;

(2)点F在CD上,且CE=EF,求证:AF⊥BD.

20.(9分)如图,☉O的内接四边形ABCD两组对边的延长线分别交于点E,F.

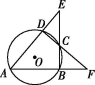
(1)若∠E=∠F,求证:∠ADC=∠ABC;

(2)若∠E=∠F=42°,求∠A的度数;

(3)若∠E=α,∠F=β,且α≠β,请你用含有α,β的代数式表示∠A的大小.

21.(9分)如图,AB是☉O的直径,AC,BC,CE是☉O的弦,PB是☉O的切线,B为切点,OP⊥BC于点D,且交☉O于点E.

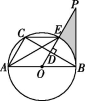
(1)求证:∠P=∠AEC;

(2)若=,CE=2,求图中由线段PB,PE及所围成的阴影部分的

面积.

22.(11分)如图,已知半径为5的☉M经过x轴上一点C,与y轴交于A,B两点,连接AM,AC,AC平分∠OAM,AO+CO=6.

(1)判断☉M与x轴的位置关系,并说明理由;

(2)求AB的长;

(3)连接BM并延长交☉M于点D,连接CD,求直线CD的解析式.

第二十四章　达标测试卷

一、选择题

1.D　2.C　3.A　4.B　5.D　6.C　7.C

8.C　解析:∵∠AIC=124°,∴∠IAC+∠ICA=56°.

∵点I是△ABC的内心,

∴∠BAC=2∠IAC,∠BCA=2∠ICA,

∴∠BAC+∠BCA=2(∠IAC+∠ICA)=2×56°=112°,

∴∠B=180°-112°=68°.

∵四边形ABCD内接于☉O,

∴∠ADC=180°-∠B=180°-68°=112°,

∴∠CDE=68°.

故选C.

9.C　解析:如图,∵△ABC是等边三角形,

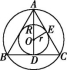
∴△ABC的内切圆和外接圆是同心圆,设圆心为点O.

由题意,知OE=OD=r,AO=R,AD=h,

∴h=R+r,故A正确.

∵AD⊥BC,

∴∠DAC=∠BAC=×60°=30°,

∴在Rt△AOE中,R=2r,故B正确.

∵OD=OE=r,AB=AC=BC=a,

∴AE=AC=a,

∴+r2=(2r)2,+=R2,

∴r=a,R=a,故C错误,D正确.

故选C.

10.C　解析:∵△ABC是等边三角形,

∴∠BAC=∠ACB=60°.

∵=,=,

∴∠ADB=∠ACB=60°,∠BDC=∠BAC=60°,

∴∠ADB=∠BDC,故①正确.

∵点D是弧AC上一动点,

∴与不一定相等,∴DA与DC不一定相等,故②错误.

当DB最长时,DB为☉O直径,∴∠BCD=90°;

∵∠BDC=60°,∴∠DBC=30°,∴DB=2DC,故③正确.

在DB上取一点E,使DE=AD,如图,∵∠ADB=60°,∴△ADE是等边三角形,∴AD=AE,∠DAE=60°;

∵∠BAC=60°,∴∠BAE=∠CAD;

∵AB=AC,∴△ABE≌△ACD(SAS),

∴BE=CD,∴BD=BE+DE=CD+AD,故④正确.

综上所述,正确的有①③④,共3个.故选C.

二、填空题

11.35　12.5　13.400π　14.2

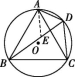
15.3　解析:如图,作点A关于CD的对称点A′,连接A′B交CD于点P′,连接OA′,则当点P在点P′处时,AP+BP有最小值,为    A′B的长.

∵OA=OB=OA′=CD=3 cm且∠AOD=2∠AOB=60°,

∴∠AOB=∠BOD=30°.

∵点A关于CD的对称点为点A′,

∴∠DOA′=∠AOD=60°,

∴∠BOA′=∠BOD+∠DOA′=90°,

∴△BOA′为等腰直角三角形,

∴A′B==3 cm,

即AP+BP的最小值为3 cm.

16.π-2　解析:如图,连接OB,过点O作OH⊥BC于点H.

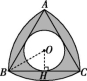
∵△ABC为等边三角形,

∴AB=BC=AC=2,∠ABC=60°.

∵☉O是△ABC的内切圆,

∴OH为☉O的半径,

∠OBH=30°.

∵点O为△ABC的内心,

∴BH=CH=1.

在Rt△OBH中,由勾股定理,得OH=.

∵S弓形AB=S扇形ACB-S△ABC,

∴S阴影=3S弓形AB+S△ABC-S☉O

=3(S扇形ACB-S△ABC)+S△ABC-S☉O

=3S扇形ACB-2S△ABC-S☉O

=3×-2××22-π·()2

=π-2.

三、解答题

17.(1)证明:∵AD∥BC,DF∥AB,

∴四边形ABED为平行四边形,

∴∠B=∠D.

∵∠AFC=∠B,∠ACF=∠D,

∴∠AFC=∠ACF,

∴AC=AF.

(2)解:连接AO,CO,如图.

由(1)得∠AFC=∠ACF,∴∠AFC==75°,

∴∠AOC=2∠AFC=150°,

∴的长l==.

18.

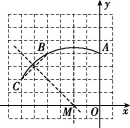
答图

解:(1)(-2,0)　(2)2　(3)内

(4)如图,由题意,得点O到☉M上最近的点在直线OM上.

∵☉M的半径长为2,OM=2,∴点O到☉M上最近的点的距离为2-2.

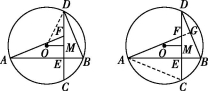
19.(1)解:连接OD,如图①.

∵M是CD的中点,CD=12,

∴DM=CD=6,OM⊥CD,∠OMD=90°,

∴Rt△OMD中,OD=,且OM=3,

∴OD==3,即圆O的半径长为3.

　　①　　　　　②

(2)证明:连接AC,延长AF交BD于点G,如图②.

∵AB⊥CD,CE=EF,∴AB是CF的垂直平分线,

∴AF=AC,即△ACF是等腰三角形.

∵CE=EF,∴∠FAE=∠CAE.

∵=,∴∠CAE=∠CDB,∴∠FAE=∠CDB.

∵在Rt△BDE中,∠CDB+∠B=90°,∴∠FAE+∠B=90°,

∴∠AGB=90°,∴AG⊥BD,即AF⊥BD.

20.(1)证明:∵∠E=∠F,∠DCE=∠BCF,∠ADC=∠E+∠DCE,

∠ABC=∠F+∠BCF,

∴∠ADC=∠ABC.

(2)解:由(1)知∠ADC=∠ABC.

又∠ADC+∠ABC=180°,

∴∠ADC=∠ABC=90°,∴∠A=90°-42°=48°.

(3)解:连接EF,如图.

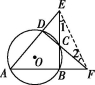
∵四边形ABCD为圆的内接四边形,∴∠ECD=∠A.

∵∠ECD=∠1+∠2,∴∠A=∠1+∠2.

∵∠A+∠1+∠2+∠AEB+∠AFD=180°,

∴2∠A+α+β=180°,∴∠A=90°-.

21.(1)证明:∵PB是☉O的切线,

∴OB⊥PB,∴∠OBP=90°,∴∠BOP+∠P=90°.

∵OP⊥BC,∴∠BOP+∠ABC=90°,∴∠ABC=∠P.

又∵∠ABC=∠AEC,∴∠P=∠AEC.

(2)解:如图,连接OC.

∵=,∴∠ABC=∠BAE.

由圆周角定理,得∠BOE=2∠BAE,

∴∠BOE=2∠ABC.

∵∠BOE+∠ABC=90°,∴∠BOE=60°,∠ABC=30°.

∵=,∴∠AOC=∠BOE=60°,∴∠COE=60°.

∵OC=OE,∴△COE为等边三角形,∴OE=CE=2.

在Rt△POB中,∠POB=60°,∴OP=4,PB=2,

∴阴影部分的面积=×2×2-=2-π.

22.解:(1)☉M与x轴相切.理由如下:如图,连接CM.

∵AC平分∠OAM,∴∠OAC=∠CAM.

又∵MC=AM,∴∠CAM=∠ACM,∴∠OAC=∠ACM,∴OA∥MC.

∵OA⊥x轴,∴MC⊥x轴.

又∵MC为☉M的半径,∴☉M与x轴相切.

(2)如图,过点M作MN⊥y轴于点N,∴AN=BN=AB.

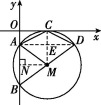
∵∠MCO=∠AOC=∠MNA=90°,∴四边形MNOC是矩形,

∴NM=OC,MC=ON=5.

设AO=m,∴OC=6-m,AN=5-m,

在Rt△ANM中,由勾股定理可知AM2=AN2+MN2,

∴52=(5-m)2+(6-m)2,解得m=2或m=9(舍去),∴AN=3,∴AB=6.

(3)如图,连接AD与CM交于点E.

∵BD是☉O的直径,∴∠BAD=90°,∴AD∥x轴,∴AD⊥MC.

由勾股定理可得AD=8,∴D(8,-2).

由(2)可得C(4,0).

设直线CD的解析式为y=kx+b,则解得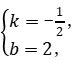

∴直线CD的解析式为y=-x+2.