


【阶段测试】人教版数学九年级上册-- 期末检测卷(含答案)
展开人教版数学九年级上册期末检测卷
(时间:120分钟 分数:120分)
一、选择题(共12道题,每小题4分,共48分)
1.下列数学符号中,既是轴对称图形又是中心对称图形的是( )
![]()
![]()
![]()
![]()
A B C D
2.下列事件属于必然事件的是( )
A.打开电视,正在播出《新闻联播》
B.若原命题成立,则它的逆命题也成立
C.一组数据的方差越小,则这组数据的波动越小
D.在数轴上任取一点,则该点表示的数是有理数
3.如图,AB是☉O的切线,点A为切点,OB交☉O于点C,点D在☉O上,连接AD,CD,OA,若∠B=20°,则∠ADC的度数为( )
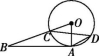
第3题图
A.40° B.35° C.30° D.20°
4.在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,-b),则ab的值为( )
A.-4 B.4 C.12 D.-12
5.下列关于二次函数y=3(x+1)(2-x)的图象和性质的叙述中,正确的是( )
A.点(0,2)在函数图象上 B.开口方向向上
C.对称轴是直线x=1 D.与直线y=3x有两个交点
6.如图,在△ABC中,CA=CB=4,∠BAC=α,将△ABC绕点A逆时针旋转2α,得到△AB′C′,连接B′C并延长交AB于点D,当
B′D⊥AB时,![]() 的长是( )
的长是( )

第6题图
A.![]() π B.
π B.![]() π C.
π C.![]() π D.
π D.![]() π
π
7.某城市为了申办冬运会,决定改善城市容貌,绿化环境,计划用两年时间,使绿地面积增加44%,这两年平均每年绿地面积的增长率是( )
A.19% B.20% C.21% D.22%
8.如图,已知正六边形ABCDEF内接于半径为r的☉O,随机地往☉O内投一粒米,落在正六边形内的概率为( )
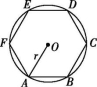
第8题图
A.![]() B.
B.![]() C.
C.![]() D.以上答案都不对
D.以上答案都不对
9.如图,直线y1=kx与抛物线y2=ax2+bx+c交于A,B两点,则抛物线y=ax2+(b-k)x+c可能是( )

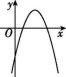
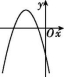
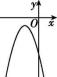
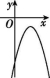
A B C D
10.如图,等边三角形OAB的边长为2![]() ,边OA在x轴正半轴上,现将等边三角形OAB绕点O逆时针旋转,每次旋转60°,则第2 022次旋转结束后,等边三角形中心的坐标为( )
,边OA在x轴正半轴上,现将等边三角形OAB绕点O逆时针旋转,每次旋转60°,则第2 022次旋转结束后,等边三角形中心的坐标为( )
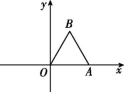
第10题图
A.(![]() ,1) B.(0,2) C.(-
,1) B.(0,2) C.(-![]() ,-1) D.(
,-1) D.(![]() ,-1)
,-1)
11.如图,四边形ABCD内接于☉O,AE⊥CB交CB的延长线于点E.若BA平分∠DBE,AD=5,CE=![]() ,则AE等于( )
,则AE等于( )
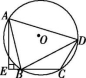
第11题图
A.3 B.3![]() C.4
C.4![]() D.2
D.2![]()
12.二次函数y=ax2+bx+c的部分图象如图,与y轴交于(0,-1),对称轴为直线x=1.下列结论:①abc>0;②a>![]() ;③对于任意实数m,都有m(am+b)>a+b成立;④若点(-2,y1),
;③对于任意实数m,都有m(am+b)>a+b成立;④若点(-2,y1),![]() ,(2,y3)在该函数图象上,则y3<y2<y1;⑤方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为4.其中正确结论有( )
,(2,y3)在该函数图象上,则y3<y2<y1;⑤方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为4.其中正确结论有( )
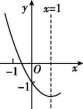
第12题图
A.2个 B.3个 C.4个 D.5个
二、填空题(共6道题,每小题4分,共24分)
13.已知圆锥的高是12,底面圆的半径为5,则这个圆锥的侧面展开图的周长为 .
14.“头盔是生命之盔”,质检部门对某工厂生产的头盔质量进行抽查,抽查结果如表:
抽查的头盔数n | 100 | 200 | 300 | 500 | 800 | 1 000 | 3 000 |
合格的头盔数m | 95 | 194 | 289 | 479 | 769 | 960 | 2880 |
合格头盔的频率 | 0.950 | 0.970 | 0.963 | 0.958 | 0.961 | 0.960 | 0.960 |
请估计该工厂生产5 000个头盔,合格的头盔数有 个.
15.一块圆形玻璃镜面碎成了几块,其中一块如图,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为 厘米.
![]()
16.已知x1,x2是一元二次方程x2-2x-12=0的两个实数根,则![]() -3x1-x2+2x1x2= .
-3x1-x2+2x1x2= .
17.规定:两个函数y1,y2的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数y1=2x+2与y2=-2x+2的图象关于y轴对称,则这两个函数互为“Y函数”.若函数y=kx2+2(k-1)x+k-3(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为 .
18.如图,已知矩形ABCD中,AD=3,AB=5,E是边DC上一点,将△ADE绕点A顺时针旋转得到△AD′E′,使得点D的对应点D′落在AE上,如果D′E′的延长线恰好经过点B,那么DE的长度等于 .

三、解答题(共7道题,共78分)
19.(8分)解方程:
(1)3(x-3)=(x-3)2;
(2)x2+4x-1=0.
20.(10分)神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成两幅不完整的统计图.
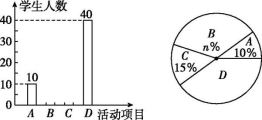
根据以上信息,解答下列问题:
(1)m= ,n= ;并补全条形统计图.
(2)根据抽样调查的结果,请估算全校1 800名学生中,大约有多少人选择参观科学馆.
(3)在选择A项活动的10人中,有甲、乙、丙、丁四名女生,现计划把这10名学生平均分成两组进行培训,每组各有两名女生,则甲、乙被分在同一组的概率是多少?
21.(10分)如图,在扇形AOB中,∠AOB=90°,C,D是![]() 上两点,过点D作DE∥OC交OB于点E,在OD上取点F,使OF=DE,连接CF并延长交OB于点G.
上两点,过点D作DE∥OC交OB于点E,在OD上取点F,使OF=DE,连接CF并延长交OB于点G.
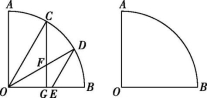
(1)求证:△OCF≌△DOE;
(2)若C,D是![]() 的三等分点,OA=2
的三等分点,OA=2![]() :
:
①求∠OGC的度数;
②请比较GE和BE的大小.
22.(12分)某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数):当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?
(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
23.(12分)已知关于x的一元二次方程x2-(k+4)x+4k=0.
(1)求证:无论k为任何实数,此方程总有两个实数根;
(2)若方程的两个实数根分别为x1,x2,且满足![]() +
+![]() =
=![]() ,求k的值;
,求k的值;
(3)若Rt△ABC的斜边的长为5,另外两条边的长恰好是方程的两个根x1,x2,求Rt△ABC的内切圆半径.
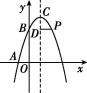
24.(13分)在平面直角坐标系xOy中,已知抛物线y=-x2+bx+c经过点A(-1,0)和点B(0,3),顶点为C,点D在其对称轴上,且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
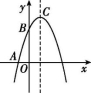
(1)求抛物线的解析式;
(2)求点P的坐标;
(3)将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,试判断在y轴上是否存在点M,使得MP+ME的值最小,若存在,求出点M的坐标;若不存在,请说明理由.
25.(13分)如图,AB为☉O的直径,CD是☉O的切线,C为切点,连接BC.ED垂直平分OB,垂足为E,且交![]() 于点F,交BC于点P,连接BF,CF.
于点F,交BC于点P,连接BF,CF.
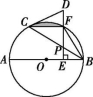
(1)求证:∠DCP=∠DPC;
(2)当BC平分∠ABF时,求证:CF∥AB;
(3)在(2)的条件下,OB=2,求阴影部分的面积.
期末检测卷
一、选择题
1.D 2.C 3.B 4.D 5.D 6.B 7.B 8.A 9.B 10.A
11.D 解析:如图,连接AC.
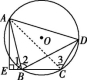
∵BA平分∠DBE,
∴∠1=∠2.
∵四边形ABCD内接于☉O,
∴∠CDA+∠CBA=180°,
∴∠1=∠CDA.
又∵∠2=∠3,∴∠3=∠CDA,
∴AC=AD=5.
∵AE⊥CB,∴∠AEC=90°,
∴AE=![]() =
=![]() =2
=2![]() .
.
故选D.
12.A 解析:∵抛物线开口向上,∴a>0.
∵抛物线与y轴交于点(0,-1),∴c=-1.
∵-![]() =1,∴b=-2a<0,∴abc>0,故①正确.
=1,∴b=-2a<0,∴abc>0,故①正确.
∵y=ax2-2ax-1,当x=-1时,y>0,∴a+2a-1>0,∴a>![]() ,故②正确.
,故②正确.
当m=1时,m(am+b)=a+b,故③错误.
∵点(-2,y1)到对称轴的距离大于点(2,y3)到对称轴的距离,∴y1>y3;∵点![]() 到对称轴的距离小于点(2,y3)到对称轴的距离,∴y3>y2,∴y2<y3<y1,故④错误.
到对称轴的距离小于点(2,y3)到对称轴的距离,∴y3>y2,∴y2<y3<y1,故④错误.
∵方程|ax2+bx+c|=k(k≥0,k为常数)的解是抛物线与直线y=±k的交点,当有3个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为3;当有4个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为4;当有2个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为2,故⑤错误.故选A.
二、填空题
13.26+10π 14.4 800 15.26 16.-14
17.y=2x-3或y=-x2+4x-4 解析:∵函数y=kx2+2(k-1)x+k-3(k为常数)的“Y函数”图象与x轴只有一个交点,∴函数y=kx2+2(k-1)x+ k-3(k为常数)的图象与x轴也只有一个交点.
当k=0时,函数解析式为y=-2x-3,它的“Y函数”解析式为y=2x-3,它们的图象与x轴只有一个交点.
当k≠0时,此函数是二次函数,∵它们的图象与x轴都只有一个交点,∴它们的顶点分别在x轴上,
∴[2(k-1)]2-4k(k-3)=0,解得k=-1,
∴原函数的解析式为y=-x2-4x-4=-(x+2)2,
∴它的“Y函数”解析式为y=-(x-2)2=-x2+4x-4.
综上所述,其“Y函数”的解析式为y=2x-3或y=-x2+4x-4.
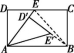
18.![]() 解析:如图,连接BE,延长D′E′到点B处.
解析:如图,连接BE,延长D′E′到点B处.
由旋转,知△AD′E′≌△ADE.
又四边形ABCD为矩形,
∴AD′=AD=3,∠AD′E′=∠D=90°.
∵D′E′的延长线恰好经过点B,∴∠AD′B=90°.
在Rt△ABD′中,BD′=![]() =
=![]() =4.
=4.
∵AB·AD=AE·BD′,
∴AE=![]() =
=![]() =
=![]() ,
,
∴在Rt△ADE中,
DE=![]() =
=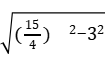 =
=![]() .
.
三、解答题
19.解:(1)移项,得3(x-3)-(x-3)2=0,
提取公因式,得(x-3)(3-x+3)=0,
则x-3=0或3-x+3=0,
解得x1=3,x2=6.
(2)移项,得x2+4x=1,
配方,得x2+4x+4=1+4,
∴(x+2)2=5,
∴x=-2±![]() ,
,
∴x1=-2+![]() ,x2=-2-
,x2=-2-![]() .
.
20.解:(1)调查学生总人数m=10÷10%=100(名),∴C组的人数为100× 15%=15(名),
∴B组人数为100-10-40-15=35(名),∴B组所占百分数为![]() ×100%= 35%,即n=35.
×100%= 35%,即n=35.
补全条形统计图如下:
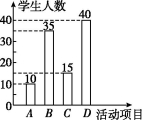
(2)1 800×![]() =720(人),
=720(人),
故大约有720人选择参观科学馆.
(3)列表如下:
女生 | 甲 | 乙 | 丙 | 丁 |
甲 | — | 甲乙 | 甲丙 | 甲丁 |
乙 | 乙甲 | — | 乙丙 | 乙丁 |
丙 | 丙甲 | 丙乙 | — | 丙丁 |
丁 | 丁甲 | 丁乙 | 丁丙 | — |
共有12种等可能的结果数,其中甲、乙被分在同一组的有4种,∴甲、乙被分在同一组的概率是![]() =
=![]() .
.
21.(1)证明:∵DE∥OC,∴∠COD=∠ODE.
在△OCF和△DOE中,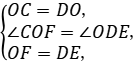 ∴△OCF≌△DOE(SAS).
∴△OCF≌△DOE(SAS).
(2)解:①∵C,D是![]() 的三等分点,∠AOB=90°,
的三等分点,∠AOB=90°,
∴∠AOC=∠COD=∠BOD=30°.
∵△OCF≌△DOE,∴∠OCF=∠DOE=30°.
∵∠COG=∠COD+∠DOB=60°,∴∠OGC=90°.
②在Rt△OGC中,∠OCG=30°,OA=OC=OB=2![]() ,∴OG=
,∴OG=![]() .
.
又∵∠DOE=30°,∴OF=2.
∵∠OCF=∠COF=30°,∴CF=OF=2.
∵△OCF≌△DOE,∴OE=CF=2,
∴GE=2-![]() ,BE=2
,BE=2![]() -2,
-2,
∴BE-GE=3![]() -4>0,∴BE>GE.
-4>0,∴BE>GE.
22.解:(1)设每天的销售量y(件)与每件售价x(元)函数关系式为y=kx+b,
由题意,得![]() 解得
解得![]()
∴y与x之间的函数关系式为y=-5x+150.
(2)根据题意,得(-5x+150)(x-8)=425,解得x1=13,x2=25(舍去),
∴若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为13元.
(3)w=y(x-8)=(-5x+150)(x-8)=-5x2+190x-1 200=-5(x-19)2+605,
∵8≤x≤15,且x为整数,当x<19时,w随x的增大而增大,
∴当x=15时,w有最大值,最大值为525.
故每件消毒用品的售价为15元时,每天的销售利润最大,最大利润是525元.
23.(1)证明:∵Δ=[-(k+4)]2-16k=k2-8k+16=(k-4)2≥0,
∴无论k为任何实数,此方程总有两个实数根.
(2)解:根据题意,得x1+x2=k+4,x1x2=4k.
∵![]() +
+![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得k=2.
经检验,k=2是分式方程![]() =
=![]() 的根.
的根.
故k的值为2.
(3)解:解方程x2-(k+4)x+4k=0,得x1=4,x2=k.
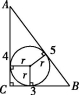
根据题意,得42+k2=52,解得k=3(负值舍去).
设Rt△ABC的内切圆半径为r,如图.
由切线长定理,得(3-r)+(4-r)=5,
解得r=1,
∴Rt△ABC的内切圆半径为1.
24.解:(1)把A(-1,0)和B(0,3)代入y=-x2+bx+c,
得![]() 解得
解得![]() ∴抛物线解析式为y=-x2+2x+3.
∴抛物线解析式为y=-x2+2x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4,∴C(1,4),抛物线的对称轴为直线x=1.
如图①,设CD=t,则D(1,4-t).
∵线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点
P处,
∴∠PDC=90°,DP=DC=t,∴P(1+t,4-t).
把P(1+t,4-t)代入y=-x2+2x+3,得-(1+t)2+2(1+t)+3=4-t,
整理,得t2-t=0,解得t1=0(舍去),t2=1,∴P(2,3).
①
(3)∵点P坐标为(2,3),顶点C坐标为(1,4),将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,∴点E坐标为(1,-1),
∴点E关于y轴的对称点F(-1,-1).
如图②,连接PF交y轴于点M,则MP+ME=MP+MF=PF的值最小.
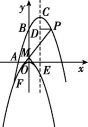
②
设直线PF的解析式为y=kx+n,则![]() 解得
解得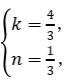
∴直线PF的解析式为y=![]() x+
x+![]() ,∴点M的坐标为
,∴点M的坐标为![]() .
.
25.(1)证明:连接OC,如图①.
∵CD是☉O的切线,C为切点,∴∠DCO=90°,即∠OCB+∠DCP=90°.
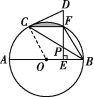
①
∵DE⊥OB,∴∠DEB=90°,∴∠OBC+∠BPE=90°.
∵OB=OC,∴∠OCB=∠OBC,∴∠DCP=∠BPE.
∵∠BPE=∠DPC,∴∠DCP=∠DPC.
(2)证明:连接OF,如图②.
∵ED垂直平分OB,∴OF=BF.
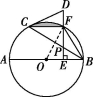
②
∵OF=OB,∴BF=OF=OB,∴△BOF是等边三角形,
∴∠FOB=∠ABF=60°,
∴∠FCB=![]() ∠FOB=30°.
∠FOB=30°.
∵BC平分∠ABF,∴∠ABC=![]() ∠ABF=30°,∴∠FCB=∠ABC,∴CF∥AB.
∠ABF=30°,∴∠FCB=∠ABC,∴CF∥AB.
(3)解:连接OF,OC,如图③.
由(2)知∠ABC=∠CBF=30°,∴∠COF=2∠CBF=60°.
∵OB=2,即☉O半径为2,∴S扇形COF=![]() =
=![]() .
.
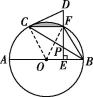
③
∵OC=OF,∠COF=60°,∴△COF是等边三角形,∴CF=OF=OB=2.
∵ED垂直平分OB,∴OE=BE=![]() OB=1,∠FEB=90°,
OB=1,∠FEB=90°,
∴在Rt△FEB中,EF=![]() =
=![]() =
=![]() ,
,
∴S△COF=![]() CF·EF=
CF·EF=![]() ×2×
×2×![]() =
=![]() ,
,
∴S阴影=S扇形COF-S△COF=![]() -
-![]() .
.
【阶段测试】湘教版数学八年级上册--期末测试数学卷(较易 含答案): 这是一份【阶段测试】湘教版数学八年级上册--期末测试数学卷(较易 含答案),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
【阶段测试】湘教版数学八年级上册--期末测试数学卷(困难 含答案): 这是一份【阶段测试】湘教版数学八年级上册--期末测试数学卷(困难 含答案),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
【阶段测试】人教版数学九年级上册-- 期中检测卷(含答案): 这是一份【阶段测试】人教版数学九年级上册-- 期中检测卷(含答案),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












