


【阶段测试】人教版数学九年级上册--第二十二章 二次函数 达标测试卷(含答案)
展开第二十二章 二次函数 达标测试卷
(时间:120分钟 分数:120分)
一、选择题(共10道题,每小题3分,共30分)
1.抛物线y=-3x2+6x+2的对称轴是( )
A.直线x=2 B.直线x=-2 C.直线x=1 D.直线x=-1
2.已知二次函数y=(a-1)x2,当x>0时,y随x增大而增大,则实数a的取值范围是( )
A.a>0 B.a>1 C.a≠1 D.a<1
3.描点法画函数图象是研究陌生函数的基本方法.对于函数y=(x-2)2,有下列说法:①图象经过点(1,1);②当x=2时,y有最小值0;③y随x的增大而增大;④该函数图象关于直线x=2对称.其中正确的是( )
A.①② B.①②④ C.①②③④ D.②③④
4.已知抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,则n的值为( )
A.-2 B.-4 C.2 D.4
5.将一抛物线先向下平移1个单位长度,再向左平移2个单位长度后所得到的新抛物线为y=-2(x-3)2+1,则这条抛物线的解析式是( )
A.y=-2(x-5)2+2 B.y=-2(x-1)2 C.y=-2(x-2)2-1 D.y=-2(x-4)2+3
6.函数y=kx2-6x+3的图象与x轴有公共点,则k的取值范围是( )
A.k<3 B.k<3且k≠0 C.k≤3且k≠0 D.k≤3
7.已知二次函数y=x2-2x-3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当-1<x1<0,1<x2<2,x3>3时,y1,y2,y3三者之间的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y1<y2 D.y2<y1<y3
8.已知二次函数y=ax2+bx-c(a≠0),其中b>0,c>0,则该函数的图象可能为( )
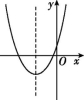
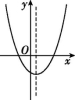

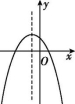
A B C D
9.如图,在平面直角坐标系中,O为坐标原点,正方形OABC的顶点A在y轴的负半轴上,点C在x轴的正半轴上,经过点A,B的抛物线y=a(x-2)2+c(a>0)的顶点为E.若△ABE为等腰直角三角形,则a的值为( )
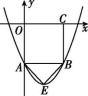
第9题图
A.1 B.2 C.![]() D.
D.![]()
10.二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论:①abc>0;②a-b+c>0;③3a+c<0;④若m为任意实数,则a+b≥am2+bm;⑤若a![]() +bx1=a
+bx1=a![]() +bx2,且x1≠x2,则x1+x2=2.其中正确的结论有( )
+bx2,且x1≠x2,则x1+x2=2.其中正确的结论有( )
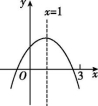
第10题图
A.2个 B.3个 C.4个 D.5个
二、填空题(共6道题,每小题3分,共18分)
11.二次函数y=-3x2-2的最大值为 .
12.已知二次函数y=-x2+2x+m的部分图象如图,则关于x的一元二次方程-x2+2x+m=0的解为 .

第12题图
13.已知一条抛物线与抛物线y=2x2+3形状相同,与另一条抛物线y=-![]() (x+1)2-2的顶点坐标相同,这条抛物线的解析式为 .
(x+1)2-2的顶点坐标相同,这条抛物线的解析式为 .
14.飞机着陆后滑行的距离s(单位:m)关于滑行时间t(单位:s)的函数解析式是s=20t-![]() t2,则飞机着陆滑行到停止,最后6 s滑行的距离是 m.
t2,则飞机着陆滑行到停止,最后6 s滑行的距离是 m.
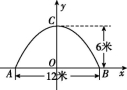
15.如图,一个横截面为抛物线形的隧道,宽12米、高6米,车辆双向通行.若规定车辆必须在中心线两侧、距离道路边缘2米的范围内行驶,并保持车辆顶部与隧道有不少于1米的空隙,则通过隧道车辆的高度限制应为 米.

第15题图
16.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2-4a>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|的图象(如图),并写出下列五个结论:①图象与坐标轴的交点为(-1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当-1≤x≤1或x≥3时,函数值y随x的增大而增大;④当x=-1 或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是 .
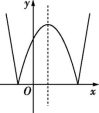
第16题图
三、解答题(共6道题,共52分)
17.(8分)已知函数y=-3(x+1)2-4.
(1)指出函数图象的开口方向、对称轴和顶点坐标.
(2)当x取何值时,该函数有最值?请求出最值.
(3)当x取何值时,y随x的增大而减小?
18.(8分)已知二次函数y=-x2+bx+c的图象如图,解答下列问题:
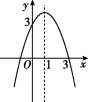
(1)关于x的一元二次方程-x2+bx+c=0的解为 .
(2)求此二次函数的解析式.
(3)当x为何值时,y<0?
(4)若直线y=k与抛物线没有交点,直接写出k的取值范围.
19.(8分)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10 m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积比为1∶2的矩形,已知栅栏的总长度为24 m,设较小矩形的宽为x m(如图).
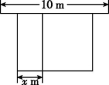
(1)若矩形养殖场的总面积为36 m2,求此时x的值.
(2)当x为多少时,矩形养殖场的总面积最大?最大值为多少?
20.(8分)某商场销售一种进价为30元/个的商品,当销售价格x(元/个)满足40<x<80时,其销售量y(万个)与x之间的关系式为y=-![]() x+9.同时销售过程中的其他开支为50万元.
x+9.同时销售过程中的其他开支为50万元.
(1)求出商场销售这种商品的净利润z(万元)关于销售价格x(元/个)的函数解析式;销售价格定为多少时,净利润最大?最大净利润是
多少?
(2)若净利润预期不低于17.5万元,试求出销售价格x的取值范围;若还需考虑销售量尽可能大,销售价格应定为多少?
21.(9分)如图,在一条笔直的滑道上有黑、白两个小球同向运动,黑球在A处开始减速,此时白球在黑球前面70 cm处.
小聪测量黑球减速后的运动速度v(单位:cm/s)、运动距离y(单位:cm)随运动时间t(单位:s)变化的数据,整理得下表.
![]()
运动时间t/s | 0 | 1 | 2 | 3 | 4 |
运动速度v/(cm/s) | 10 | 9.5 | 9 | 8.5 | 8 |
运动距离y/cm | 0 | 9.75 | 19 | 27.75 | 36 |
小聪探究发现,黑球的运动速度v与运动时间t之间成一次函数关系,运动距离y与运动时间t之间成二次函数关系.
(1)求出v关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围).
(2)当黑球减速后运动距离为64 cm时,求它此时的运动速度.
(3)若白球一直以2 cm/s的速度匀速运动,黑球在运动过程中会不会碰到白球?请说明理由.
22.(11分)已知:如图,抛物线y=ax2+4x+c经过原点O(0,0)和点A(3,3),P为抛物线上的一个动点,过点P作x轴的垂线,垂足为B(m,0),并与直线OA交于点C.
(1)求抛物线的解析式.
(2)当点P在直线OA上方时,求线段PC长度的最大值.
(3)如图②,过点A作AD⊥x轴于点D,在抛物线上是否存在点P,使得以P,A,C,D四点为顶点的四边形是平行四边形?若存在,求m的值;若不存在,请说明理由.

①
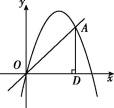
②
第二十二章 达标测试卷
一、选择题
1.C 2.B 3.B 4.B 5.A 6.D 7.D 8.C
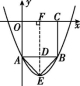
9.D 解析:∵抛物线y=a(x-2)2+c(a>0)的顶点为E,且经过点A,B,
∴抛物线的对称轴是直线x=2,且点A,B关于直线x=2对称.
如图,过点E作EF⊥x轴于点F,交AB于点D.
∵△ABE为等腰直角三角形,∴AD=BD=2,
∴AB=4,DE=![]() AB=2.
AB=2.
∵四边形OABC是正方形,
∴OA=AB=BC=OC=4,∴EF=4+2=6,
∴A(0,-4),E(2,-6).
把点A,E的坐标代入y=a(x-2)2+c,得a=![]() .
.
故选D.
10.B 解析:∵抛物线开口向下,∴a<0;
∵抛物线的对称轴为直线x=-![]() =1,∴b=-2a>0;
=1,∴b=-2a>0;
∵抛物线与y轴的交点在x轴上方,
∴c>0,∴abc<0,∴①错误.
∵抛物线与x轴的一个交点在(2,0)与(3,0)之间,
∴抛物线与x轴的另一个交点在(-1,0)与(0,0)之间,
∴当x=-1时,y<0,即a-b+c<0,∴②错误.
∴a+2a+c<0,即3a+c<0,∴③正确.
∵x=1时,y有最大值,∴a+b+c≥am2+bm+c,
∴a+b≥am2+bm,∴④正确.
∵a![]() +bx1=a
+bx1=a![]() +bx2,
+bx2,
∴a(x1+x2)(x1-x2)+b(x1-x2)=0,
∴(x1-x2)[a(x1+x2)+b]=0;
∵x1≠x2,∴a(x1+x2)+b=0,
∴x1+x2=-![]() =-
=-![]() =2,∴⑤正确.
=2,∴⑤正确.
故选B.
二、填空题
11.-2 12.x1=-1,x2=3
13.y=2(x+1)2-2或y=-2(x+1)2-2 14.18
15.![]() 解析:建立如图的平面直角坐标系.
解析:建立如图的平面直角坐标系.
根据题意,得A(-6,0),B(6,0),C(0,6).
设抛物线解析式为y=ax2+6,
把B(6,0)代入解析式,得
36a+6=0,解得a=-![]() ,
,
∴抛物线的解析式为y=-![]() x2+6.
x2+6.
当x=4时,y=-![]() ×42+6=
×42+6=![]() ,
,![]() -1=
-1=![]() ,
,
∴通过隧道车辆的高度限制应为![]() 米.
米.
16.4 解析:∵点(-1,0),(3,0)和(0,3)的坐标都满足函数y=|x2-2x-3|,∴①是正确的;
从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线x=1,∴②是正确的;
根据函数的图象和性质,发现当-1≤x≤1或x≥3时,函数值y随x的增大而增大,∴③是正确的;
函数图象的最低点就是与x轴的两个交点,根据y=0,求出相应的x的值为x=-1或x=3,∴④是正确的;
从图象上看,当x<-1或x>3时,函数值中有大于x=1时y的值,∴⑤是不正确的.
综上所述,正确结论的个数是4.
三、解答题
17.解:(1)∵-3<0,
∴函数图象开口向下,顶点坐标为(-1,-4),对称轴为直线x=-1.
(2)∵函数图象开口向下,
∴函数有最大值.
∵顶点坐标为(-1,-4),
∴当x=-1时,函数有最大值,最大值为-4.
(3)∵-3<0,对称轴为直线x=-1,
∴当x>-1时,y随x的增大而减小.
18.解:(1)x1=-1,x2=3
(2)设二次函数的解析式为y=-(x-1)2+k.
∵二次函数图象与x轴交于点(3,0),
∴-(3-1)2+k=0,解得k=4,
∴二次函数的解析式为y=-(x-1)2+4,
即二次函数的解析式为y=-x2+2x+3.
(3)若y<0,则函数的图象在x轴的下方,由函数的图象可知x>3或x<-1.
(4)若直线y=k与抛物线没有交点,则k大于函数的最大值,即k>4.
19.解:(1)根据题意,知较大矩形的宽为2x m,长为![]() =(8-x)m.
=(8-x)m.
根据题意,得(x+2x)(8-x)=36,解得x=2或x=6.
当x=6时,3x=18>10,不符合题意,舍去,∴x=2.
答:此时x的值为2.
(2)设矩形养殖场的总面积是y m2.
∵墙的长度为10 m,∴0<x≤![]() .
.
根据题意,得y=(x+2x)(8-x)=-3x2+24x=-3(x-4)2+48.
∵-3<0,∴当x=![]() 时,y取最大值,最大值为-3×
时,y取最大值,最大值为-3×![]() +48=
+48=![]() .
.
答:当x=![]() 时,矩形养殖场的总面积最大,最大值为
时,矩形养殖场的总面积最大,最大值为![]() m2.
m2.
20.解:(1)z=y(x-30)-50=![]() (x-30)-50=-
(x-30)-50=-![]() x2+12x-320,
x2+12x-320,
当x=-![]() =60时,z最大,最大值为-
=60时,z最大,最大值为-![]() ×602+12×60-320=40.
×602+12×60-320=40.
∴销售价格定为60元/个时,净利润最大,最大净利润是40万元.
(2)当z=17.5时,17.5=-![]() x2+12x-320,解得x1=45,x2=75.
x2+12x-320,解得x1=45,x2=75.
∵净利润预期不低于17.5万元,且-![]() <0,∴45≤x≤75.
<0,∴45≤x≤75.
∵y=-![]() x+9,y随x的增大而减小,∴x=45时,销售量最大.
x+9,y随x的增大而减小,∴x=45时,销售量最大.
∴销售价格应定为45元/个.
21.解:(1)设v=mt+n,将(0,10),(2,9)代入,
得![]() 解得
解得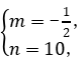 ∴v=-
∴v=-![]() t+10.
t+10.
设y=at2+bt+c,将(0,0),(2,19),(4,36)代入,
得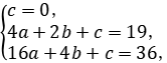 解得
解得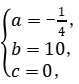 ∴y=-
∴y=-![]() t2+10t.
t2+10t.
(2)令y=64,即-![]() t2+10t=64,解得t=8或t=32.
t2+10t=64,解得t=8或t=32.
当t=8时,v=6;当t=32时,v=-6(舍去).
∴当黑球减速后运动距离为64 cm时,它的运动速度为6 cm/s.
(3)不会.理由如下:
设黑、白两球间的距离为w cm,根据题意可知,
w=70+2t-y=![]() t2-8t+70=
t2-8t+70=![]() (t-16)2+6.
(t-16)2+6.
∵![]() >0,∴当t=16时,w的值最小为6,
>0,∴当t=16时,w的值最小为6,
∴黑、白两球间的最小距离为6 cm,大于0 cm,∴黑球不会碰到白球.
22.解:(1)把O(0,0)和A(3,3)代入y=ax2+4x+c,得![]() 解得
解得![]()
∴抛物线的解析式为y=-x2+4x.
(2)由题意得0<m<3.
∵B(m,0),PB⊥x轴,点P在抛物线y=-x2+4x上,
∴P(m,-m2+4m).
∵O(0,0),A(3,3),∴直线OA的解析式为y=x,
∴点C(m,m),∴PB=-m2+4m,CB=m,
∴PC=PB-CB=-m2+4m-m=-m2+3m=-(m-![]() )2+
)2+![]() .
.
∵-1<0,∴抛物线开口向下,∴函数有最大值,∴当点B的坐标为(![]() ,0)时,PC最大=
,0)时,PC最大=![]() .
.
故当点P在直线OA的上方时,线段PC长度的最大值是![]() .
.
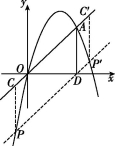
(3)存在.∵A(3,3),AD⊥x轴,∴AD=3.
当点P在直线OA的上方时,线段PC长度的最大值是![]() .
.
∴点P在直线OA的下方.
如图,过点D作DP∥OA交抛物线于点P和点P′,此时四边形ADPC和四边形ADP′C′是平行四边形.
∵直线OA的解析式为y=x,∴直线DP的解析式为y=x-3.
由 解得
解得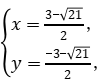 或
或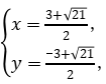 ∴m的值为
∴m的值为![]() .
.
【阶段测试】人教版数学九年级上册--第二十四章 圆 达标测试卷(含答案): 这是一份【阶段测试】人教版数学九年级上册--第二十四章 圆 达标测试卷(含答案),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
【阶段测试】人教版数学九年级上册--第二十三章 旋转 达标测试卷(含答案): 这是一份【阶段测试】人教版数学九年级上册--第二十三章 旋转 达标测试卷(含答案),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
人教版数学九年级上册第二十二章达标测试卷2: 这是一份人教版数学九年级上册第二十二章达标测试卷2,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













