【阶段测试】人教版数学九年级上册--第二十三章 旋转 达标测试卷（含答案）

第二十三章  旋转　 达标测试卷

（时间：120分钟  分数：120分）

一、选择题(共10道题,每小题3分,共30分)

1.下列图案中既是中心对称图形又是轴对称图形的是(　  　)

              A         B         C         D

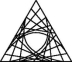
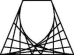
2.在下列四种图形变换中,如图图案包含的变换是(　  　)

第2题图

A.旋转和轴对称 B.轴对称和平移

C.平移和旋转 D.平移、旋转和轴对称

3.将△ABC绕点O逆时针旋转90°后得到的图案应该是(　  　)

                A        B        C       D

4.如图,将直角三角板ABC绕顶点A顺时针旋转到△AB′C′,点B′恰好落在CA的延长线上,∠B=30°,∠C=90°,则∠BAC′为(　  　)

第4题图

A.90° B.60° C.45° D.30°

5.如图,△DEF是由△ABC绕点O旋转180°得到的,则下列结论不成立的是(　  　)

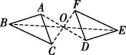
第5题图

A.点A与点D是对应点 B.BO=EO   C.∠ACB=∠FED   D.AB∥DE

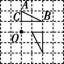
6.如图,在平面直角坐标系中,点B,C,E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是(　  　)

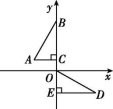
第6题图

A.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度

B.△ABC绕点C顺时针旋转90°,再向下平移1个单位长度

C.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度

D.△ABC绕点C顺时针旋转90°,再向下平移3个单位长度

7.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为(　  　)

A.2 B.2  C.4 D.2

第7题图

8.在如图的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则点P2的坐标为(　  　)

第8题图

A.(1.4,1) B.(1.5,2) C.(1.6,1) D.(2.4,1)

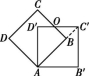
9.如图,把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是(　  　)

第9题图

A.6  B.6   C.3  D.3+3

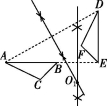
10.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别是点D,E,F是边AC的中点,连接BF,BE,FD,FD与CE交于点G.则下列结论错误的是(　  　)

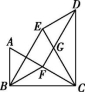
第10题图

A.BE=BC   B.BF∥DE,BF=DE  C.∠DFC=90° D.DG=3GF

二、填空题(共6道题,每小题3分,共18分)

11.已知点P(-b,2)与点Q(3,2a)关于原点对称,则a+b的值是　 　.

12.如图,分别以正方形的各边为直径向其内部作半圆,将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角度最小是　        　. 

第12题图

13.如图,将正方形网格放置在平面直角坐标系中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(-1,1),C(3,1).△A′B′C′是△ABC关于x轴的对称图形,将△A′B′C′绕点B′逆时针旋转180°,点A′的对应点为M,则点M的坐标为　         　. 

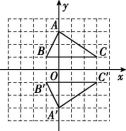
第13题图

14.如图,已知在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,现将AB绕点B顺时针旋转90°得到BD,连接CD,则△BCD的面积为　  　. 

第14题图

15.如图,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°,将△ADE绕点D逆时针旋转90°得到△CDM.若AE=1,则MF的长为　        . 

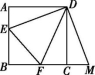
第15题图

16.如图,已知A,B是线段MN上的两点,MN=12,MA=3,MB>3,以点A为中心顺时针旋转点M,以点B为中心逆时针旋转点N,使M,N两点重合成一点C,构成△ABC,当△ABC为直角三角形时,AB的长度是　       　.

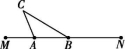
第16题图

三、解答题(共6道题,共52分)

17.(8分)我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心.

(1)如图①,△ABC≌△DEF,△DEF能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心;若不能,试简要说明理由.(保留必要的作图痕迹)

(2)如图②,△ABC≌△MNK,△MNK能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心;若不能,试简要说明理由.(保留必要的作图痕迹)

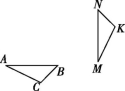
①          ②

题图

18.(8分)如图,在△ABC中,BA=BC,∠ABC=40°,将△ABC绕点B按逆时针方向旋转100°,得到△DBE,连接AD,CE交于点F.

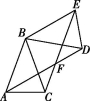
(1)求证:△ABD≌△CBE;

(2)求∠AFC的度数.

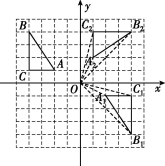
19.(8分)在如图的正方形网格中,△ABC的顶点均在格点上,请解决下列问题:

(1)作出△ABC关于原点O对称的△A1B1C1,并写出点B1的坐标;

(2)作出△A1B1C1绕点O逆时针旋转90°得到的△A2B2C2,并写出线段C1C2的长度.

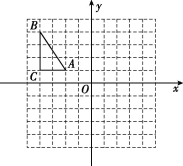
题图

20.(8分)如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.

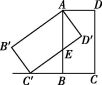
(1)求证:BC=BC′;

(2)若AB=2,BC=1,求AE的长.

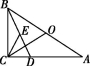
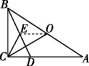
21.(9分)在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.

(1)如图①,连接OC,请写出∠OCE和∠OAC的数量关系并说明理由.

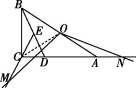
(2)如图②,点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.猜想并证明线段OM和线段ON之间的数量关系.

①          ②

题图

22.(11分)平移、旋转、翻折是几何图形的最基本的三种图形变换,利用图形变换可将分散的条件相对集中,以达到解决问题的目的.

(1)探究发现:如图①,P是等边三角形ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.

完成下面的解题过程:

解:将△APC绕点A旋转到△AP′B的位置,连接PP′,则△APP′是

　　　　三角形. 

∵PP′=PA=3,PB=4,P′B=PC=5,∴P′P2+PB2=P′B2,∴△BPP′为　　　　三角形,且∠BPP′=90°. 

∴∠APB=∠BPP′+∠APP′=　　　　°+　　　　°=　　　　°. 

(2)类比延伸:如图②,在正方形ABCD内部有一点P,连接PA,PB,PC.若PA=2,PB=4,∠APB=135°,求PC的长.

(3)拓展迁移:如图③,若点P是正方形ABCD外一点,PA=3,PB=1,PC=,求∠APB的度数.

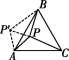
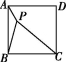
                     ①      ②      ③

第二十三章　达标测试卷

一、选择题

1.A　2.A　3.A　4.B　5.C　6.D　7.A

8.C　解析:∵点A(2,4),A1(-2,1),

∴点P(2.4,2)平移后的对应点P1为(-1.6,-1).

∵点P1绕点O逆时针旋转180°,得到对应点P2,

∴点P2的坐标为(1.6,1).

故选C.

9.A　解析:如图,连接BC′.

∵旋转角∠BAB′=45°,∴∠BAD′=45°,

∴点B在对角线AC′上.

∵B′C′=AB′=3,

在Rt△AB′C′中,AC′==3,

∴BC′=3-3.

在等腰直角三角形OBC′中,OB=BC′=3-3,

∴OC′=(3-3)=6-3,

∴OD′=3-OC′=3-3,

∴四边形ABOD′的周长是2AD′+OB+OD′=6+3-3+3-3=6.故选A.

10.D　解析:A.由旋转的性质可知,CB=CE,∠BCE=60°,∴△BCE为等边三角形,∴BE=BC,本选项结论正确,不符合题意.

B.在Rt△ABC中,∠ABC=90°,∠ACB=30°,F是边AC的中点,∴AB=AC=CF=BF.

由旋转的性质可知,CA=CD,∠ACD=60°,

∴∠A=∠ACD.

在△ABC和△CFD中,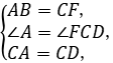

∴△ABC≌△CFD(SAS),∴DF=BC=BE.

∵DE=AB=BF,∴四边形EBFD为平行四边形,

∴BF∥DE,BF=DE,本选项结论正确,不符合题意.

C.∵△ABC≌△CFD,∴∠DFC=∠ABC=90°,本选项结论正确,不符合  题意.

D.在Rt△GFC中,∠GCF=30°,∴GF=CF,同理可得,DF=CF,∴DF=3GF,故本选项结论错误,符合题意.故选D.

二、填空题

11.2　12.90°　13.(-2,1)　14.8

15.　解析:∵△ADE绕点D逆时针旋转90°得到△CDM,

∴∠A=∠DCM=90°,DE=DM,∠ADE=∠CDM,

∴∠FCM=∠FCD+∠DCM=180°,

∴F,C,M三点共线.

∵∠EDM=∠EDC+∠CDM=∠EDC+∠ADE=90°,∠EDF=45°,

∴∠FDM=∠EDF=45°.

又∵DF=DF,∴△DEF≌△DMF(SAS),∴EF=MF.

设EF=MF=x.

∵AE=CM=1,且BC=3,

∴BM=BC+CM=3+1=4,

∴BF=BM-MF=BM-EF=4-x.

∵EB=AB-AE=3-1=2,

∴在Rt△EBF中,由勾股定理得EB2+BF2=EF2,

即22+(4-x)2=x2,解得x=,∴MF=.

16.4或5　解析:设AB=x,则BC=BN=9-x.

在△ABC中,AC=AM=3,

由三角形两边之和大于第三边,得

解得3<x<6.

①若AC为斜边,则32=x2+(9-x)2,即x2-9x+36=0,

方程无解,故AC为斜边不成立.

②若AB为斜边,则x2=(9-x)2+32,解得x=5,满足3<x<6.

③若BC为斜边,则(9-x)2=32+x2,解得x=4,满足3<x<6.

∴x=5或x=4.

三、解答题

17.

①         ②

答图

解:(1)能.如图①,点O1就是所求作的旋转中心.

(2)能.如图②,点O2就是所求作的旋转中心.

18.(1)求证:△ABD≌△CBE;

(2)求∠AFC的度数.

(1)证明:∵△ABC绕点B按逆时针方向旋转100°,

∴∠ABD=∠CBE=100°.

∵BA=BC,∴AB=BC=BD=BE.

在△ABD和△CBE中,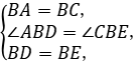

∴△ABD≌△CBE(SAS).

(2)解:∵∠ABD=∠CBE=100°,BA=BC=BD=BE,

∴∠BAD=∠ADB=∠BCE=∠BEC=40°.

∵∠ABE=∠ABD+∠DBE=140°,

∴∠AFE=360°-∠ABE-∠BAD-∠BEC=140°,

∴∠AFC=180°-∠AFE=40°.

19.

答图

解:(1)如图,△A1B1C1即为所作,点B1的坐标为(4,-4).

(2)如图,△A2B2C2即为所作,线段C1C2的长度为=.

20.(1)证明:连接AC,AC′,如图.

∵四边形ABCD为矩形,∴∠ABC=90°,即AB⊥CC′.

∵将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,

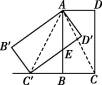
∴AC=AC′,∴BC=BC′.

(2)解:∵四边形ABCD为矩形,

∴AD=BC,∠D=∠ABC′=90°.

∵BC=BC′,∴BC′=AD.

∵将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,

∴AD=AD′,∠D′=∠D,∴AD′=BC′=BC=1,∠ABC′=∠D′.

在△AD′E和△C′BE中,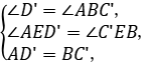

∴△AD′E≌△C′BE,∴BE=D′E.

设AE=x,则D′E=BE=2-x.

在Rt△AD′E中,∠D′=90°,

由勾股定理,得x2-(2-x)2=1,解得x=,∴AE=.

21.

①          ②

答图

解:(1)∠OCE=∠OAC.理由如下:如图①,连接OE.

∵∠BCA=90°,BE=ED,BO=OA,

∴CE=BE=DE=BD,CO=OA=OB,∴∠OCA=∠A,OE∥AD,OE=AD,

∴∠EOC=∠OCA.

∵BD=AD,∴CE=EO,∴∠EOC=∠OCE,∴∠OCE=∠OAC.

(2)OM=ON.证明如下:如图②,连接CO.

∵OC=OA,DA=DB,∴∠OAC=∠OCA=∠ABD,∴∠COA=∠ADB.

∵∠MON=∠ADB,∴∠AOC=∠MON,∴∠COM=∠AON.

∵∠ECO=∠OAC,∴∠MCO=∠NAO.

在△COM和△AON中,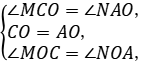∴△COM≌△AON(ASA),

∴OM=ON.

22.解:(1)等边　直角　90　60　150

(2)如图①,把△ABP绕点B顺时针旋转90°得到△CBP′,连接PP′,

则P′B=PB=4,P′C=PA=2.

①

∵旋转角是90°,∴∠PBP′=90°,∴△BPP′是等腰直角三角形,

∴PP′=PB=4,∠PP′B=45°.

∵∠APB=135°,∴∠CP′B=∠APB=135°,

∴∠PP′C=135°-45°=90°.

在Rt△PP′C中,由勾股定理,得PC==6.

(3)如图②,将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,

则△ABP′≌△CBP,∠PBP′=90°,BP′=BP=1,AP′=CP=,

②

∴∠BPP′=45°.根据勾股定理,得PP′=BP=.

∵AP=3,∴AP2+PP′2=9+2=11.

∵AP′2=()2=11,∴AP2+PP′2=AP′2,∴△APP′是直角三角形,且∠APP′=90°,∴∠APB=∠APP′-∠BPP′=90°-45°=45°.