


【同步练习】高中数学人教A版(2019)选修第一册--1.1.1空间向量及其线性运算 练习(含解析)
展开人教A版(2019)选修一1.1.1空间向量及其线性运算
(共17题)
一、选择题(共10题)
- 下面关于空间向量的说法正确的是

A.若向量 ![]() ,
,![]() 平行,则
平行,则 ![]() ,
,![]() 所在直线平行
所在直线平行
B.若向量 ![]() ,
,![]() 所在直线是异面直线,则
所在直线是异面直线,则 ![]() ,
,![]() 不共面
不共面
C.若 ![]() ,
,![]() ,
,![]() ,
,![]() 四点不共面,则向量
四点不共面,则向量 ![]() ,
,![]() 不共面
不共面
D.若 ![]() ,
,![]() ,
,![]() ,
,![]() 四点不共面,则向量
四点不共面,则向量 ![]() ,
,![]() ,
,![]() 不共面
不共面
- 如图,在空间四边形
 中,设
中,设 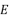 ,
, 分别是
分别是  ,
,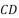 的中点,则
的中点,则 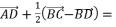

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 空间中任意四个点
 ,
,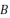 ,
,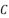 ,
,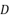 ,则
,则 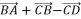 等于
等于 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 若
 ,
, ,
, 三点在同一条直线上,则
三点在同一条直线上,则 
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
- 已知正方体
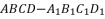 的棱长为
的棱长为 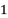 ,设
,设  ,
, ,
, ,则
,则 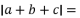

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知向量
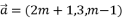 ,
, ,且
,且  ,则实数
,则实数 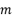 的值等于
的值等于 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或 ![]()
- 已知点
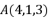 ,
,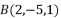 ,
,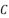 为线段
为线段 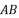 上一点,且
上一点,且  ,则点
,则点 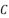 的坐标为
的坐标为 
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
- 已知
 的三个顶点坐标分别为
的三个顶点坐标分别为 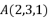 ,
,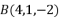 ,
,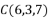 ,则
,则  的重心坐标为
的重心坐标为 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知
 ,
,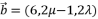 ,若
,若  ,则
,则  与
与  的值可以是
的值可以是 
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
- 已知
 ,
,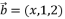 ,且
,且  ,则
,则  的值为
的值为 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(共4题)
- 已知
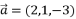 ,
,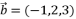 ,
, ,若
,若 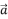 ,
,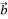 ,
, 三向量共面,则
三向量共面,则  .
.
- 在空间四边形
 中,若
中,若  是正三角形,且
是正三角形,且 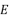 为其中心,连接
为其中心,连接 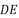 ,则
,则  的化简结果为 .
的化简结果为 .
- 已知
 ,
, ,
, 是不共面向量,
是不共面向量, ,
, ,
,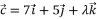 ,若
,若 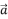 ,
,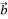 ,
, 三个向量共面,则实数
三个向量共面,则实数  等于 .
等于 .
- 已知
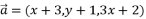 ,
, ,若
,若  ,则
,则 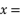 ,
,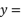 .
.
三、解答题(共3题)
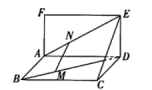
- 如图,点
 ,
,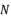 分别在对角线
分别在对角线 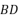 ,
,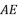 上,且
上,且 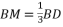 ,
, .求证:向量
.求证:向量  ,
, ,
, 共面.
共面.
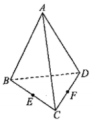
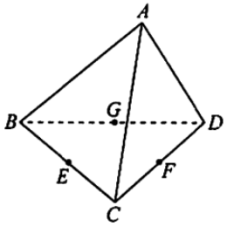
- 如图,已知空间四边形
 ,连接
,连接 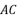 ,
,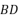 ,
,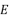 ,
, ,
,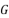 分别是
分别是  ,
,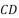 ,
,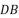 的中点.请化简以下式子,并在图中标出化简结果的向量.
的中点.请化简以下式子,并在图中标出化简结果的向量.
(1) ![]() ;
;
(2) ![]() .
.
- 如图所示,在正方体
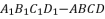 中,
中,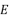 ,
, 分别是
分别是  ,
,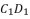 的中点,求证:
的中点,求证: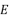 ,
, ,
,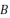 ,
,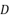 四点共面.
四点共面.

答案
一、选择题(共10题)
1. 【答案】D
【解析】我们可以通过平移将空间中任意两个向量平移到一个平面内,因此空间任意两个向量都是共面的,故B,C都不正确.由向量平行与直线平行的区别,可知A不正确.因为 ![]() ,
,![]() ,
,![]() 是空间中共端点
是空间中共端点 ![]() 但不共面的三条线段,所以向量
但不共面的三条线段,所以向量 ![]() ,
,![]() ,
,![]() 不共面.
不共面.
2. 【答案】C
【解析】因为 ![]() ,
,![]() ,所以
,所以 ![]() .
.
3. 【答案】C
【解析】如图,
利用平面向量运算法则即可得出 ![]() .
.

4. 【答案】A
【解析】因为 ![]() ,
,![]() ,
,![]() 三点共线,所以向量
三点共线,所以向量 ![]() ,
,![]() 共线.
共线.
又因为 ![]() ,
,![]() ,
,
所以 ![]() ,
,
解得 ![]() ,
,![]() .
.
5. 【答案】D
【解析】利用向量加法的平行四边形法则,结合正方形的性质,可得 ![]() .
.
6. 【答案】B
【解析】当 ![]() 时,
时,![]() ,
,![]() ,
,![]() 与
与 ![]() 不平行,所以
不平行,所以 ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,解得
,解得 ![]() .
.
7. 【答案】C
8. 【答案】B
【解析】设 ![]() 的重心坐标为
的重心坐标为 ![]() ,则
,则 ![]() ,
,![]() ,
,![]() .
.
所以 ![]() 的重心坐标为
的重心坐标为 ![]() .
.
9. 【答案】A
【解析】因为 ![]() ,
,
所以 ![]() ,
,
即 ![]() ,
,
所以 ![]()
解得 ![]() 或
或 ![]()
10. 【答案】B
【解析】因为 ![]() ,
,![]() ,
,
所以 ![]() ,
,![]() .
.
又因为 ![]() ,
,
所以 ![]() ,
,
解得 ![]() ,
,![]() ,
,
所以 ![]() .
.
二、填空题(共4题)
11. 【答案】 ![]()
【解析】由题意知 ![]() ,
,
即 ![]() ,
,
所以 ![]()
解得 ![]() .
.
12. 【答案】 ![]()
【解析】延长 ![]() ,交
,交 ![]() 于点
于点 ![]() ,则
,则 ![]() 为
为 ![]() 的中点,
的中点,
所以 ![]() ,
,![]() ,
,
所以 ![]() .
.
13. 【答案】 ![]()
【解析】若向量 ![]() ,
,![]() ,
,![]() 共面,则存在
共面,则存在 ![]() ,使得
,使得 ![]() ,
,
所以 ![]() ,
,
所以 ![]()
解得 ![]() .
.
14. 【答案】 ![]() ;
; ![]()
三、解答题(共3题)
15. 【答案】由题图知,
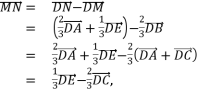
所以向量 ![]() ,
,![]() ,
,![]() 共面.
共面.
16. 【答案】
(1) ![]() ,
,
如图中向量 ![]() .
.
(2) 
如图中向量 ![]() .
.
17. 【答案】设 ![]() ,
,![]() .
.
则 ![]() ,
,
![]() ,
,
所以 ![]() ,
,
而 ![]() ,
,![]() ,
,![]() ,
,![]() 四点不共线,
四点不共线,
因此 ![]() ,故
,故 ![]() ,
,![]() ,
,![]() ,
,![]() 四点共面.
四点共面.
数学选择性必修 第一册1.1 空间向量及其运算综合训练题: 这是一份数学选择性必修 第一册1.1 空间向量及其运算综合训练题,共21页。试卷主要包含了直三棱柱中,若,,,则,已知三棱锥中,是的中点,则,已知点,,,向量,则点坐标是等内容,欢迎下载使用。
高中数学第一章 空间向量与立体几何1.1 空间向量及其运算优秀测试题: 这是一份高中数学第一章 空间向量与立体几何1.1 空间向量及其运算优秀测试题,共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算课时作业: 这是一份人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算课时作业,共6页。试卷主要包含了判断下列各命题的真假等内容,欢迎下载使用。













