





专题6 数据与统计图表(知识解读)-七年级数学下册《同步考点解读•专题训练》(浙教版)
展开专题6 数据与统计图表(知识解读)
【学习目标】
1.体验数据收集、整理、描述和分析的过程,了解统计的意义;
2.能根据统计表中的数据提出并答复简单的问题,同时能够进行简单的分析。根据统计表的数据提出有价值的数学问题及解决策略。
【知识点梳理】
考点1:数据的收集
(1)方式:问卷调查、访谈、查阅资料、实地调查、试验、网上搜索等(根据具体情况合理地选择数据收集的方式)
(2)步骤:(1)明确调查的问题和目的;(2)确定调查对象;(3)选择调查方式;(4)设计调查问题;()展开调查;(6)收集并整理数据;(7)分析数据,得出结论
考点2:普查和抽样调查
(1)普查:对所有考察对象进行全面调查叫普查
优点:可以直接获得总体情况;
缺点:总体中个体数目较多时,普查的工作量较大
(2)总体:所要考察的对象的全体叫总体
个体:组成总体的每一个考察对象叫做个体
(3)抽样调查:从总体中抽取部分个体进行调查,这种调查叫做抽样调查
优点:调查范围小,节省时间、人力、物力及财力
缺点:没有普查得到的结果准确
样本:从总体中抽取的部分个体叫做总体的一个样本,为了获得较为准确的调查结果,抽样时要注意样本的代表性和广泛性
考点3:统计图的选用
扇形统计图
概念:用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小
特点:
(1)反映具体问题中的部分与总体的数量关系
(2)只能得到各部分的百分比,得不到具体数量
(3)在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360度的比
绘制扇形统计图的步骤:计算各部分占总体的百分比;计算各部分对应的扇形的圆心角的度数;画出扇形统计图,表上百分比;写出扇形统计图的名称
条形统计图:一般是由两条互相垂直的数轴和若干长方形组成,两条数轴分别表示两个不同的项目,长方形的高表示其中一个项目的数据
特点:能清楚地表示出每个项目的具体数据
折线统计图:用折线的起伏表示数据的增减变化
考点4:频数分布表和频数直方图
(1)频数:在数据统计中每个对象出现的次数称为频数
(2)注意:频数能反映每个对象出现的频繁程度;所有对象的频数之和等于数据总数
(3)频数分布:各种随机事件在n次试验中出现的次数分布。
(4)频数分布表:对一批数据,将其频数分布用表格的形式表示出来就构成了频数分布表.
(5)绘制频数直方图的步骤:计算所给数据的最大值与最小值的差;决定组距和组数;确定分点;列频数分布表;绘制频数直方图
(6)频数直方图:是一种特殊的条形统计图,它将统计对象的数据进行了分组,画在横轴上;纵轴(即长方形的高)表示各组数据的频数
(7)频数直方图的优点:能更清晰、更直观地反映数据的整体状况。
统计图的选择:
条形统计图:清楚地表示每个项目的具体数目
折线统计图:清楚地反映事物的变化情况
扇形统计图:清楚地表示出各部分在总体中所占的百分比
频数直方图:能更清晰、更直观地反映数据的整体状况
【典例分析】
【考点1:数据的收集】
【典例1】为了解某市5万名学生平均每天完成课后作业的时间,请你运用数学的统计知识将统计的主要步骤进行排序:
①得出结论,提出建议;
②分析数据;
③从5万名学生中随机抽取500名学生,调查他们平均完成课后作业的时间;
④利用统计图表将收集的数据整理和表示.
合理的排序是( )
A.③②④① B.③④②① C.③④①② D.②③④①
【答案】B
【解答】解:统计的主要步骤依次为:
③从5万名学生中随机抽取400名学生,调查他们平均每天读书的时间;
④利用统计图表将收集的数据整理和表示;
②分析数据;
①得出结论,提出建议.
即合理的排序是③④②①,
故选:B.
【变式1】实施“双减”政策后,为了解我县初中生每天完成家庭作业所花时间及质量情况,根据以下四个步骤完成调查:①收集数据;②制作并发放调查问卷;③分析数据;④得出结论,提出建议和整改意见.你认为这四个步骤合理的先后排序为( )
A.①②③④ B.①③②④ C.②①③④ D.②③④①
【答案】C
【解答】解:在统计调查中,我们利用调查问卷收集数据,利用表格整理数据,利用统计图描述数据,通过分析表和图来了解情况,最后得出结论,提出建议和整改意见.
因此合理的排序为:②①③④.
故选:C.
【典例2】(2022秋•贵池区期末)今年某校有2000名学生参加线上学习,为了解这些学生的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.2000名学生是总体
B.每位学生的数学成绩是个体
C.这100名学生是总体的一个样本
D.100名学生是样本容量
【答案】B
【解答】解:A、2000名学生的数学成绩是总体,故选项不合题意;
B、每位学生的数学成绩是个体,故选项符合题意;
C、这100名学生的数学成绩是总体的一个样本,故选项不合题意;
D、样本容量是100,故选项不合题意;
故选:B.
【变式2】要调查某校七年级学生每天用于完成家庭作业的时长,选取的调查对象最合适的是( )
A.选取一个班级的学生
B.选取50名男生
C.选取50名女生
D.随机选取50名七年级学生
【答案】D
【解答】解:要调查某校七年级学生每天用于完成家庭作业的时长,选取的调查对象最合适的是随机选取50名七年级学生.
故选:D.
【典例3】下列调查活动适合使用全面调查的是( )
A.调查初一某班同学课外体育锻炼时间
B.调查全市植树节中栽植树苗的成活率
C.调查某种品牌照明灯的使用寿命
D.调查抗美援朝纪录片《为了和平》在线收视率
【答案】A
【解答】解:A.调查初一某班同学课外体育锻炼时间,适合全面调查,故本选项符合题意;
B.调查全市植树节中栽植树苗的成活率,适合抽样调查,故本选项不符合题意;
C.调查某种品牌照明灯的使用寿命,适合抽样调查,故本选项不符合题意;
D.调查抗美援朝纪录片《为了和平》在线收视率,适合抽样调查,故本选项不符合题意.
故选:A.
【变式3】(2022秋•禅城区期末)要调查下列问题,适合采用抽样调查的是( )
A.疫情期间,了解全校师生入校时体温情况
B.检测我国研制的C919大飞机的零件的质量
C.了解一批灯泡的使用寿命
D.了解小明某周每天参加体育运动的时间
【答案】C
【解答】解:A.疫情期间,了解全校师生入校时体温情况,适合全面调查,故本选项不合题意;
B.检测我国研制的C919大飞机的零件的质量,适合采用全面调查,故本选项不合题意;
C.了解一批灯泡的使用寿命,适合采用抽样调查,故本选项符合题意;
D.了解小明某周每天参加体育运动的时间,适合采用全面调查,故本选项不合题意;
故选:C.
【考点2:频数与频率】
【典例4】某渔民为估计池塘里鱼的总数,先随机打捞20条鱼给它们分别作上标志,然后放回,待有标志的鱼完全混合于鱼群后,第二次打捞80条,发现其中2条鱼有标志从而估计该池塘有鱼( )
A.1000条 B.800条 C.600条 D.400条
【答案】B
【解答】解:设该鱼塘有鱼x条,
根据题意得=,
解得:x=800,
经检验x=800是原分式方程的解,
即估计该鱼塘有鱼800条,
故选:B.
【变式4-1】(2022秋•兰山区校级期末)不透明的袋子中装有10个黑球和若干个白球,这些球除颜色外无其他差别.从袋子中随机摸出一球记下其颜色,再把它放回袋子中摇匀,重复上述过程,共试验400次,其中有300次摸到白球,由此估计袋子中的白球大约有( )
A.6个 B.10个 C.15个 D.30个
【答案】D
【解答】解:设白球有x个,
根据题意得:=,
解得:x=30,
经检验x=30是分式方程的解,
即白球有30个,
故选:D.
【变式4-2】(2022秋•益阳期末)从一口鱼塘里随机捞出10条鱼,在这些鱼身上做上记号,然后把鱼放回鱼池.过一段时间后,在同样的地方再捞出100条鱼,其中带有记号的鱼有2条,根据抽样调查的方法,估计整个鱼塘约有鱼 条.
【答案】500
【解答】解:设整个鱼塘约有鱼x条,由题意得:
100:2=x:10,
解得:x=500.
答:整个鱼塘约有鱼500条.
【考点3:统计图表】
【典例5】新冠肺炎疫情是一场突发的公共卫生事件,某同学收集了2021年1月份石家庄每天新增确诊病例、患者年龄等情况,为了了解每天新增确诊人数的变化趋势以及儿童感染人数所占的比例,分别选择合适的统计图是( )
A.条形统计图,扇形统计图
B.折线统计图,扇形统计图
C.折线统计图,条形统计图
D.条形统计图,频数分布直方图
【答案】B
【解答】解:某同学收集了2021年1月份石家庄每天新增确诊病例、患者年龄等情况,为了了解每天新增确诊人数的变化趋势以及儿童感染人数所占的比例,分别选择合适的统计图是折线统计图,扇形统计图.
故选:B.
【变式5-1】(2022秋•济南期末)要直观介绍空气中各成分的百分比,最适合使用的计图是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
【答案】C
【解答】解:要直观介绍空气中各成分的百分比,最适合使用的统计图是扇形统计图,
故选:C.
【变式5-2】下列四个统计图中,用来表示不同品种的奶牛的日平均产奶量最为合适的是( )
A. B.
B.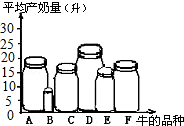
C.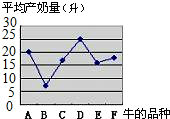 D.
D.
【答案】D
【解答】解:根据题意可得,
用来表示不同品种的奶牛的日平均产奶量最为合适的是条形统计图,因为条形统计图能很好反应不同品种奶牛的平均产量.
故选:D.
【变式5-3】疾控中心统计冬季流感疫情,既想知道每天患病人数的多少,又要能反映疫情变化的情况和趋势,最好选用( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
【答案】B
【解答】解:疾控中心统计冬季流感疫情,既想知道每天患病人数的多少,又要能反映疫情变化的情况和趋势,最好选用折线统计图,
故选:B.
【典例6】(2022秋•万源市校级期末)某校随机抽取部分学生,对“学习习惯”进行问卷调查.设计的问题:对自己做错的题目进行整理、分析、改正;答案选项为:A.很少,B.有时,C.常常,D.总是.将调查结果的数据进行了整理、绘制成部分统计图:

请根据图中信息,解答下列问题:
(1)填空:a= %,b= %,“常常”对应扇形的圆心角度数为 ;
(2)请你补全条形统计图;
(3)若该校有3000名学生,请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生各有多少名?
【解答】解:(1)44÷22%=200(人),
a=24÷200=12%,
b=72÷200=36%,
360°×30%=108°,
故答案为:12,36,108°;
(2)200×30%=60(人),补全条形统计图如图所示:

(3)3000×30%=900(人),3000×36%=1080(人),
答:“常常”对错题进行整理、分析、改正的有900人,
“总是”对错题进行整理、分析、改正的有1080人.
【变式6-1】(2022秋•朝阳区校级期末)为丰富同学们的课余生活,某校计划举行亲近大自然户外活动,现随机抽取了部分学生进行你最想去的景点是“?”的问卷调查,要求学生必须从A(南湖公园),B(净月潭森林公园),C(长春动植物园),D(北湖湿地公园)四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图,请完成下列问题:

(1)求本次调查的学生人数;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中A(南湖公园)项目的圆心角度数.
【解答】解:(1)66÷55%=120(人),
∴本次调查的学生人数为120人;
(2)C的人数为120﹣18﹣66﹣6=30(人),
补全条形统计图如下:
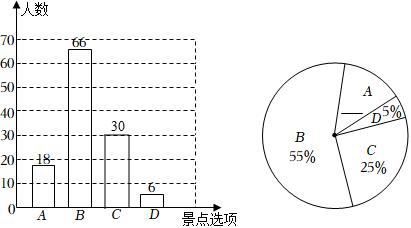
(3)360°×=54°,
答:扇形统计图中A(南湖公园)项目的圆心角度数为54°.
【变式6-2】2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某学校开设了“烹饪、种菜、家用小电器维修、课桌椅维修”4个班级,随机调查了部分学生,并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图(均不完整).请根据统计图中的信息.

解答下列问题:
(1)本次抽查的样本容量是 ;
(2)在扇形统计图中,“课桌椅维修”对应的圆心角为度;
(3)将条形统计图补充完整;
(4)如果该校初中学生共有2000名,那么选择“种菜”的学生约有多少人?
【解答】解:(1)224÷40%=560(人),
故答案为:560;
(2)360°×=108°,
答:在扇形统计图中,“课桌椅维修”对应的圆心角为108°;
(3)种菜的有560﹣84﹣168﹣224=84(人),
补全条形统计图如下:
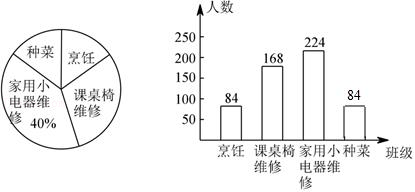
(4)2000×=300(人),
答:选择“种菜”的学生约有300人
【考点4:频数直方图】
【典例7】(2022秋•管城区校级期末)今年12月4日是第八个国家宪法日,宪法是国家的根本大法,是治国安邦的总章程.为贯彻落实习近平总书记关于宪法学习宣传教育的系列重要指示精神,某校开展了丰富多彩的宪法宣传教育活动,并分别在活动前后举办了有关学宪法的知识竞赛(百分制),活动结束后,在七年级随机抽取25名学生活动前后的竞赛成绩进行整理和描述,下面给出部分信息:活动后被抽取学生竞赛成绩为:82,88,96,98,84,86,89,99,94,90,79,91,99,98,87,92,86,99,98,84,93,88,94,89,98.
活动后被抽取学生竞赛成绩频数分布表
成绩x(分) | 频数(人) |
75≤x<80 | 1 |
80≤x<85 | 3 |
85≤x<90 | 7 |
90≤x<95 | m |
95≤x<100 | n |
请你根据以上信息解决下列问题:
(1)本次调查的样本容量是 ,表中m= ;n= ;
(2)若想直观地反映出活动前后被抽取学生竞赛成绩的变化情况,应该把数据整理,绘制成 统计图;(填“扇形”“条形”或“折线”)
(3)若90分及以上都属于A等级,根据调查结果,请估计该校2000名同学中活动后的竞赛成绩为A等级的学生有多少人?
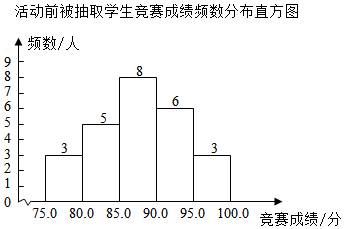
【解答】解:(1)本次调查的样本容量是25,表中m=6,n=8,
故答案为:25,6,8;
(2)若想直观地反映出活动前后被抽取学生竞赛成绩的变化情况,应该把数据整理,绘制成折线统计图,
故答案为:折线;
(3)2000×=1120(人),
答:该校2000名同学中活动后的竞赛成绩为A等级的学生有1120人.
【变式7-1】(2022春•武宣县期末)某市举行“传承好家风征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了不完整的两幅统计图表.
征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
60≤m<70 | 38 | 0.38 |
70≤m<80 | a | 0.32 |
80≤m<90 | b | c |
90≤m≤100 | 10 | 0.1 |
合计 |
| 1 |
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中a+b的值是 ;c的值是 ;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
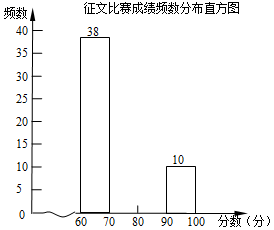
【解答】解:(1)10÷0.1=100,a+b=100﹣(38+10)=52,
c=1﹣0.38﹣0.32﹣0.1=0.2,
故答案为:52,0.2;
(2)a=100×0.32=32,b=100×0.2=20,
补全征文比赛成绩频数分布直方图如下:
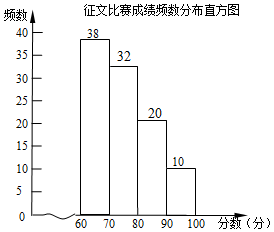
(3)1000×(0.2+0.1)=300(篇),
答:全市获得一等奖征文的篇数为300篇.
【变式7-2】(2022•新乡模拟)体育理化考试在即,某学校教务处为了调研学生的体育理化真实水平.随机抽检了部分学生进模拟测试(体育70,理化30,满分100).
【收集数据】
85,95,88,68,88,86,95,93,87,93,98,99,88,100,97,80,85,92,94,84,80,78,90,98,85,96,98,86,93,80,86,100,82,78,98,88,100,76,88,99(单位:分)
【整理数据】
成绩(单位:分) | 频数(人数) |
60≤x<70 | 1 |
70≤x<80 | m |
80≤x<90 | n |
90≤x≤100 | 19 |
【分析数据】
(1)本次抽查的学生人数共 名;
(2)填空:m= ,n= ,补充完整频数分布直方图;
(3)若分数在90≤x≤100的为优秀,估计全校九年级1200名学生中优秀的人数;
(4)针对这次模拟测试成绩.写出几条你的看法.
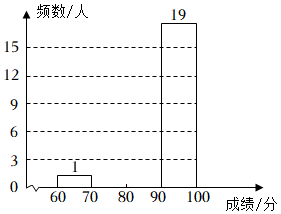
【解答】解:(1)本次抽查的学生人数共40名;
故答案为:40;
(2)由题意,得m=3,n=17,
补全频数分布直方图如下:
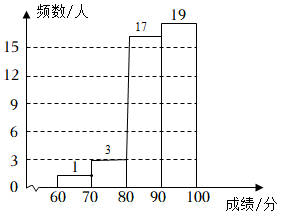
故答案为:3;17;
(3)1200×=570(人),
答:估计全校九年级1200名学生中优秀的人数为570人;
(4)①分数在优秀级别的人数占总人数的一半;②约一半的学生成绩还由提升为优秀的空间;③成绩较差的学生可通过改变体育考试项目得到适当的提高.









