第13章轴对称综合训练试题（Word版附解析）

这是一份第13章轴对称综合训练试题（Word版附解析），共5页。
第十三章综合训练一、选择题1.下列说法正确的是(　　)A.如果两个三角形全等,那么它们必是关于某条直线成轴对称B.如果两个三角形关于某条直线成轴对称,那么它们是全等三角形C.等腰三角形是关于腰上的中线成轴对称的图形D.一条线段是关于经过该线段中点的直线成轴对称的图形2.下列“慢行通过,注意危险,禁止行人通行,禁止非机动车通行”四个交通标志图(黑白阴影图片)为轴对称图形的是(　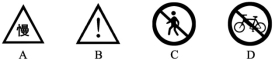　)3.如图,把等腰直角三角形ABC沿BD折叠,使点A落在边BC上的点E处.下面结论错误的是(　　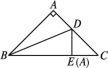)A.AB=BE B.AD=DCC.AD=DE D.AD=EC4.如图,△AOD与△BOC关于直线l成轴对称,则下列说法不正确的是(　　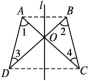)A.∠1=∠2B.∠3=∠4C.l垂直平分AB,CDD.AC,BD互相平分5.在平面直角坐标系中,若点P关于x轴的对称点在第二象限,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为(　　)A.(-3,-2) 　B.(-2,-3) 　　C.(2,3) 　D.(3,2)6.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,AB与ED相交于点F,有下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确的有(　　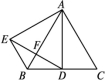)A.0个 B.1个 C.2个 D.3个7.在Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长是(　　)A.2 cm B.4 cm C.8 cm D.16 cm8.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是(　　)A.(-3,2) B.(2,-3) C.(1,-2) D.(-1,2)二、填空题9.若等腰三角形有一个角是50°,则另两个角分别是　　　　　　　　　　　. 10.如图,由镜子中的号码得出实际号码是　　　　　　. 11.如图,在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠ACB=80°,则∠BCE的度数是　　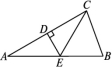　　　. 12.如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD的三等分点.若△ABC的面积为12 cm2,则图中阴影部分的面积是　　　 cm2. 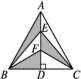三、解答题13.由边长为1的小正方形组成的方格图如图所示,AB=5.(1)请在方格图中建立平面直角坐标系,使点A的坐标为(3,3),点B的坐标为(-1,0); (2)在x轴上画点C,使△ABC是以AB为腰的等腰三角形,并写出所有满足条件的点C的坐标.(不写作法,保留作图痕迹) 14.如图,在△ABC中,∠ACB=90°,D是BC延长线上的一点,E是AB上的一点,且在BD的垂直平分线EG上,DE交AC于点F,求证:点E在AF的垂直平分线上.15.如图,△ABC和△BDE均为等边三角形,点E在线段AD上,求证:BD+CD=AD.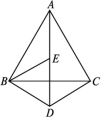               16.如图,在四边形纸片ABCD中,AD∥BC,AD=2,BC=6,∠B=60°,将纸片沿AE折叠,点B恰好与点D重合,求CE的长.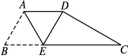
第十三章综合训练一、选择题1.B　全等的三角形不一定成轴对称,而成轴对称的两个三角形一定是全等的.2.B3.B4.D　因为成轴对称的两个图形全等,对应点的连线被对称轴垂直平分,所以选项A,B,C是正确的.5.A　因为点P关于x轴的对称点在第二象限,所以点P在第三象限,由点P到x轴的距离为2,到y轴的距离为3,得P(-3,-2).6.D7.C8.B　如图,点A的对应点A2的坐标是(2,-3).故选B.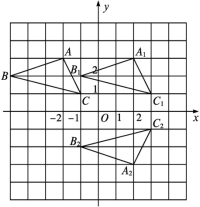二、填空题9.50°,80°或65°,65°　①当50°的角为顶角时,底角为(180°-50°)÷2=65°;②当50°的角为底角时,另一个底角是50°,顶角为180°-2×50°=80°.10.326511.50°12.6三、解答题13.解(1)所作图形如图所示.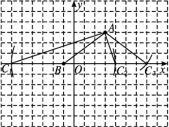(2)以AB为腰的等腰三角形有△ABC1,△ABC2,△ABC3,其中点C的坐标分别为C1(-6,0),C2(4,0),C3(7,0).14.证明如图,∵点E在BD的垂直平分线EG上,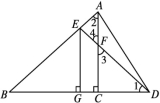∴EB=ED,∴∠1=∠B.又∠ACB=90°,∴∠1+∠3=90°,∠B+∠2=90°,∴∠3=∠2.又∠3=∠4,∴∠2=∠4,∴EA=EF,∴点E在AF的垂直平分线上.15.证明∵△ABC和△BDE均为等边三角形,∴AB=BC,BE=BD=DE,∠ABC=∠DBE=60°.∵∠ABC-∠EBC=∠DBE-∠EBC,∴∠ABE=∠CBD,∴△EBA≌△DBC.∴AE=CD.∴BD+CD=DE+AE=AD.16.解因为点B与点D关于AE对称,所以∠BAE=∠EAD,AB=AD=2.因为AD∥BC,∠B=60°,所以∠BAD=180°-∠B=120°.所以∠BAE=∠BAD=×120°=60°.所以∠BEA=60°.所以∠B=∠BEA=∠BAE=60°.所以BE=AB=2.所以CE=BC-BE=6-2=4.