高考数学一轮复习作业本6.3 基本不等式及其应用（含答案）

2020高考数学(理数)复习作业本6.3

基本不等式及其应用

一         、选择题

1.设△ABC的内角A，B，C所对的边分别为a，b，c，且C=，a＋b=12，则△ABC面积的最大值为(　　)

A．8            B．9           C．16           D．21

2.若实数a，b满足＋=，则ab的最小值为(　　)

A.            B．2         C．2          D．4

3.已知x＞0，y＞0，且4x＋y=xy，则x＋y的最小值为(　　)

A．8            B．9         C．12            D．16

4.设a>0,若关于x的不等式≥5在(1,+∞)上恒成立,则a的最小值为(　　  )

A.16                      B.9                                 C.4                                  D.2

5.正实数ab满足+=1，则(a+2)(b+4)的最小值为(  )                                         

A.16                            B.24                          C.32                            D.40

6.设正实数x,y,z满足x2-3xy+4y2-z=0,则当取得最大值时,的最大值为(　　)　　　　　　 　　　　　　 　　　　　　

A.0                                   B.1                                   C.                                      D.3

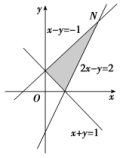
7.若x，y满足约束条件且目标函数z=ax＋by(a＞0，b＞0)的最大值为7，

则＋的最小值为(　　)

A．14           B．7        C．18           D．13

8.正实数ab满足+=1，则(a+2)(b+4)的最小值为(　　)                                         

A.16               B.24                              C.32                           D.40

二         、填空题

9.已知实数x，y满足2x﹣y=4，则4x+(0.5)y的最小值为　            

10.若点A（3，1）在直线mx+ny+1=0上，其中mn＞0,则的最大值为     .

11.若直线过点（1,2），则2a+b的最小值为        .

12.已知直线过点(1,1)，则ab的最小值为_______________．

13.直线l经过点P（1，9），且与两坐标轴的正半轴相交，当两截距之和最小时直线l的方程

为　              

14.已知a，b∈R，且a－3b＋6=0，则2a＋的最小值为________．

三         、解答题

15.首届世界低碳经济大会在南昌召开，本届大会以“节能减排，绿色生态”为主题．某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=x2－200x＋80 000，且每处理一吨二氧化碳得到可利用的化工产品价值为100元．

(1)该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？

(2)该单位每月能否获利？如果获利，求出最大利润；如果不获利，则需要国家至少补贴多少元才能使该单位不亏损？

16.某食品厂定期购买面粉，已知该厂每天需用面粉6 t，每吨面粉的价格为1 800元，面粉的保管等其他费用为平均每吨每天3元，购买面粉每次需支付运费900元．

(1)求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？

(2)若提供面粉的公司规定：当一次性购买面粉不少于210 t时，其价格可享受9折优惠(即原价的90%)，问该厂是否应考虑接受此优惠条件？请说明理由．

答案解析

1.答案为：B.

解析：由三角形的面积公式：S=absin C=ab≤×=9，

当且仅当a=b=6时等号成立．则△ABC面积的最大值为9.

2.答案为：C.

解析：由＋=知a＞0，b＞0，所以=＋≥2，即ab≥2，

当且仅当，即a=，b=2时取“=”，所以ab的最小值为2.

3.答案为：B.

解析：由题意可得＋=1，则x＋y=(x＋y)=5＋＋≥5＋2=9，

当且仅当=，即x=3，y=6时等号成立，故x＋y的最小值为9.

4.答案为：C；

5.C.

6.答案为：B；

7.答案为：B.

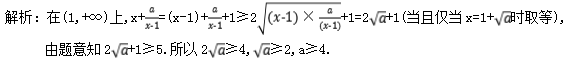
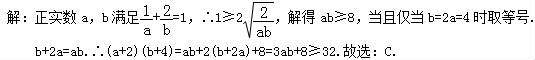
解析：画出可行域如图所示，由图形可知当直线经过x－y=－1与2x－y=2的交点N(3，4)时，

目标函数取得最大值，即3a＋4b=7，

于是＋=(3a＋4b)=(25＋＋)≥(25＋2)=7，

即＋的最小值为7.

8.C.                                         

9.答案为：8．

10.答案为：-l6;

11.答案为：8.

12.答案为：4；

13.答案为：3x+y﹣12=0．

14.答案为：0.25；

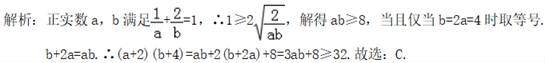
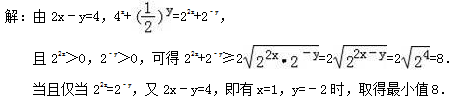
解析：∵a－3b＋6=0，∴a－3b=－6，∴2a＋=2a＋2－3b≥2=2=2=.

当且仅当2a=2－3b，即a=－3，b=1时，2a＋取得最小值.

15.解：

(1)由题意可知，二氧化碳每吨的平均处理成本为：

=x＋－200≥2－200=200，

当且仅当x=，即x=400时等号成立，

故该单位月处理量为400吨时，才能使每吨的平均处理成本最低，最低成本为200元．

(2)不获利．设该单位每月获利为S元，

则S=100x－y=100x－=－x2＋300x－80 000=－(x－300)2－35 000，

因为x∈[400，600]，所以S∈[－80 000，－40 000]．

故该单位每月不获利，需要国家每月至少补贴40 000元才能不亏损．

16.解：

(1)设该厂应每隔x天购买一次面粉，其购买量为6x t，由题意知，

面粉的保管等其他费用为3[6x＋6(x－1)＋…＋6×2＋6×1]=9x(x＋1)元．

设每天所支付的总费用为y1元，则

y1=[9x(x＋1)＋900]＋6×1 800=＋9x＋10 809≥2＋10 809=10 989.

当且仅当9x=，即x=10时取等号．

所以该厂每隔10天购买一次面粉，才能使平均每天所支付的总费用最少．

(2)若该厂家利用此优惠条件，则至少每隔35天购买一次面粉．

设该厂利用此优惠条件后，每隔x(x≥35)天购买一次面粉，平均每天支付的总费用为y2，

则y2=[9x(x＋1)＋900]＋6×1 800×0.90=＋9x＋9 729(x≥35)．

令f(x)=x＋(x≥35)，x2＞x1≥35，

则f(x1)－f(x2)=－=.

∵x2＞x1≥35，

∴x1－x2＜0，x1x2－100＞0，

∴f(x1)－f(x2)＜0，即f(x1)＜f(x2)．

∴当x=35时，y2有最小值，约为10 069.7，此时y2＜10 989.

∴该厂应该接受此优惠条件．