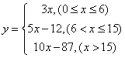高考数学一轮复习作业本1.11 函数模型及其应用（含答案）

2020高考数学(理数)复习作业本1.11 函数模型及其应用

一         、选择题

1.某产品的总成本y(万元)与产量x(台)之间的函数关系式为y=3 000＋20x－0.1x2(0＜x＜240，x∈N*)，若每台产品的售价为25万元，则生产者不亏本时(销售收入不小于总成本)的最低产量是(　　)

A．100台          B．120台         C．150台          D．180台

2.一水池有两个进水口，一个出水口，每个水口的进、出水速度如图甲、乙所示．某天0点到6点，该水池的蓄水量如图丙所示．

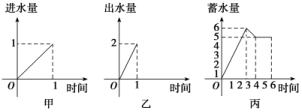
给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水，则一定正确的是(　　)

A．①            B．①②             C．①③          D．①②③

3.某市生产总值连续两年持续增加．第一年的增长率为p，第二年的增长率为q，则该市这两年生产总值的年平均增长率为(　　)

A.                  B．

C.                  D．－1

4.某校甲、乙两食堂某年1月营业额相等，甲食堂的营业额逐月增加，并且每月的增加值相同；乙食堂的营业额也逐月增加，且每月增加的百分率相同．已知本年9月份两食堂的营业额又相等，则本年5月份(　　)

A．甲食堂的营业额较高

B．乙食堂的营业额较高

C．甲、乙两食堂的营业额相同

D．不能确定甲、乙哪个食堂的营业额较高

5.某市家庭煤气的使用量x(m3)和煤气费f(x)(元)满足关系f(x)=

已知某家庭2018年前三个月的煤气费如表：

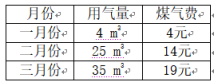
若四月份该家庭使用了20 m3的煤气，则其煤气费为(　　)

A．11.5元          B．11元         C．10.5元          D．10元

6.某家具的标价为132元，若降价以九折出售(即优惠10%)，仍可获利10%(相对于进价)，则该家具的进价是(　　)

A．118元          B．105元          C．106元          D．108元

7.某食品的保鲜时间y(单位：小时)与储藏温度x(单位：℃)满足函数关系y=ekx＋b(e=2.718…为自然对数的底数，k，b为常数)．若该食品在0 ℃的保鲜时间是192小时，在22 ℃的保鲜时间是48小时，则该食品在33 ℃的保鲜时间是(　　)

A．16小时           B．20小时          C．24小时           D．28小时

8.某品牌电视新品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y(单位：台)与投放市场的月数x之间关系的是(　　)

A．y=100x　       B．y=50x2－50x＋100    C．y=50×2x       D．y=100log2x＋100

二         、填空题

9.拟定甲、乙两地通话m分钟的电话费(单位：元)由f(m)=1.06(0.5[m]＋1)给出，其中m＞0，[m]是不超过m的最大整数(如[3]=3，[3.7]=3，[3.1]=3)，则甲、乙两地通话6.5分钟的电话费为________元．

10.某人计划购买一辆A型轿车，售价为14.4万元，购买后轿车一年的保险费、汽油费、年检费、停车费等约需2.4万元，同时汽车年折旧率约为10%(即这辆车每年减少它的价值的10%)，那么，大约使用________年后，花费在该车上的费用(含折旧费)达到14.4万元．

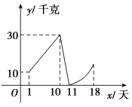
11.某人根据经验绘制了2018年春节前后，从12月21日至1月8日自己种植的西红柿的销售量y(千克)随时间x(天)变化的函数图象，如图所示，则此人在12月26日大约卖出了西红柿________千克．

12.已知一容器中有A，B两种菌，且在任何时刻A，B两种菌的个数乘积为定值1010，为了简单起见，科学家用PA=lg (nA)来记录A菌个数的资料，其中nA为A菌的个数，现有以下几种说法：

①PA≥1；

②若今天的PA值比昨天的PA值增加1，则今天的A菌个数比昨天的A菌个数多了10个；

③假设科学家将B菌的个数控制为5万个，则此时5＜PA＜5.5.

其中正确的说法为________．(写出所有正确说法的序号)

三         、解答题

13.某车间生产一种仪器的固定成本是7500元，每生产一台该仪器需要增加投入100元，已知总收入满足函数：，其中x是仪器的月产量．

(利润=总收入-总成本).

(1)将利润表示为月产量x的函数；

(2)当月产量为何值时，车间所获利润最大？最大利润是多少元？

14.为了保护水资源，提倡节约用水，某市对居民生活用水收费标准如下：每户每月用水不超过6吨时每吨3元，当用水超过6吨但不超过15吨时。超过部分每吨5元，当用水超过15吨时，超过部分每吨10元.

(1)求水费y(元)关于用水量x(吨)之间的函数关系式；

(2)若某居民某月所交水费为93元，试求此用户该月的用水量.

15.据市场分析，南雄市精细化工园某公司生产一种化工产品，当月产量在10吨至25吨时，月生产总成本y(万元)可以看成月产量x(吨)的二次函数；当月产量为10吨时，月总成本为20万元；当月产量为15吨时，月总成本最低为17.5万元，为二次函数的顶点．写出月总成本y(万元)关于月产量x(吨)的函数关系．

已知该产品销售价为每吨1.6万元，那么月产量为多少时，可获最大利润？

16.某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需要增加投入100元，已知总收益满足函数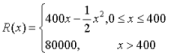：其中x是仪器的月产量．当月产量为何值时，公司所获得利润最大？最大利润是多少？

答案解析

1.答案为：C.

解析：设利润为f(x)万元，

则f(x)=25x－(3 000＋20x－0.1x2)=0.1x2＋5x－3 000(0＜x＜240，x∈N*)．

令f(x)≥0，得x≥150，∴生产者不亏本时的最低产量是150台．

2.答案为：A.

解析：由甲、乙两图知，进水速度是出水速度的，所以0点到3点不出水，3点到4点也可能一个进水口进水，一个出水口出水，但总蓄水量降低，4点到6点也可能两个进水口进水，一个出水口出水，一定正确的是①.

3.答案为：D.

解析：设第一年年初生产总值为1，则这两年的生产总值为(p＋1)(q＋1)．

设这两年生产总值的年平均增长率为x，则(1＋x)2=(p＋1)(q＋1)，

解得x=－1，故选D.

4.答案为：A.

设甲、乙两食堂1月份的营业额均为m，甲食堂的营业额每月增加a(a＞0)，乙食堂的营业额每月增加的百分率为x，由题意可得，m＋8a=m×(1＋x)8，则5月份甲食堂的营业额y1=m＋4a，乙食堂的营业额y2=m×(1＋x)4=，因为y－y=(m＋4a)2－m(m＋8a)=16a2＞0，所以y1＞y2，故本年5月份甲食堂的营业额较高．

5.答案为：A.

解析：根据题意可知f(4)=C=4，f(25)=C＋B(25－A)=14，f(35)=C＋B(35－A)=19，

解得A=5，B=，C=4，所以f(x)=

所以f(20)=4＋(20－5)=11.5.

6.答案为：D.

解析：设家具的进价为a元，由题意知132×(1－10%)－a=10%·a，解得a=108.故选D.

7.答案为：C.

解析：由已知条件，得192=eb，∴b=ln 192.又∵48=e22k＋b=e22k＋ln 192=192e22k=192(e11k)2，

∴e11k===.

设该食品在33 ℃的保鲜时间是t小时，则t=e33k＋ln 192=192 e33k=192(e11k)3=192×=24(小时)．

8.答案为：C.

解析：根据函数模型的增长差异和题目中的数据可知，应为指数型函数模型，代入数据验证即可.

一         、填空题

9.答案为：4.24；

解析：∵m=6.5，∴[m]=6，则f(m)=1.06×(0.5×6＋1)=4.24.

10.答案为：4；

解析：设使用x年后花费在该车上的费用达到14.4万元，

依题意可得，14.4(1－0.9x)＋2.4x=14.4.

化简得：x－6×0.9x=0，令f(x)=x－6×0.9x.

因为f(3)=－1.374＜0，f(4)=0.063 4＞0，

所以函数f(x)在(3，4)上应有一个零点．

故大约使用4年后，花费在该车上的费用达到14.4万元．

11.答案为：；

解析：前10天满足一次函数关系，设为y=kx＋b，将点(1，10)和点(10，30)代入函数解析式得

解得k=，b=，所以y=x＋，则当x=6时，y=.

12.答案为：③；

解析：当nA=1时PA=0，故①错误；

若PA=1，则nA=10，若PA=2，则nA=100，故②错误；

设B菌的个数为nB=5×104，∴nA==2×105，∴PA=lg(nA)=lg 2＋5.

又∵lg 2≈0.3，∴5＜PA＜5.5，故③正确．

二         、解答题

13.解：

14.解：(1)； (2)18吨；

15.解：

16.解：