高考数学一轮复习作业本7.2 直线、平面的平行关系（含答案）

2020高考数学(理数)复习作业本7.2

直线、平面的平行关系

一         、选择题

1.a和b是两条异面直线，下列结论正确的是(　)

A、过不在a、b上的任意一点，可作一个平面与a、b都平行

B、过不在a、b上的任意一点，可作一条直线与a、b都相交

C、过不在a、b上的任意一点，可作一条直线与a、b都平行

D、过a可以并且只可以作一个平面与b平行

2.如果点M是两条异面直线外的一点，则过点M且与a，b都平行的平面              （   ）

A、只有一个                                 B、恰有两个   C、或没有，或只有一个                    D、有无数个

3.若，则l与m的关系是（   ）

A、；    B、l与m异面；  C、；   D、

4.a,b是两条不相交的直线，则过直线b且平行于a的平面（    ）

A、有且只有一个     B、至少有一个     C、至多有一个     D、只能有有限个

5.若，，则下列说法正确的是（    ）

A、过在平面内可作无数条直线与平行

B、 过在平面内仅可作一条直线与平行

C、 过在平面内可作两条直线与平行

D、 与的位置有关

6.下列四个命题

（1），

（2），

（3），

（4），

正确有（    ）个

A、               B、            C、             D、

7.如图，在正方体ABCD-A1B1C1D1中，M，N分别是A1B，AC的中点，则MN与平面BB1C1C的位置关系是(    )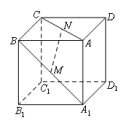

A.相交           B.平行       C.垂直             D.不能确定  

8.若a，b，a∥，条件甲是“a∥b”，条件乙是“b∥”，则条件甲是条件乙的                                                                                   （   ）

A、充分不必要条件              B、必要不充分条件

C、充要条件                   D、既不充分又不必要条件

二         、填空题

9.过平面外一点，与平面平行的直线有_________条，如果直线m∥平面，那么在平面内有_________条直线与m平行

10.若P是直线l外一点，则过P与l平行的平面有___________个。

11.n平面，则m∥n是m∥的______条件

12.若直线  a ∥平面 ，直线b∥ 平面，a，b,则a、b的位置关系是＿

三         、解答题

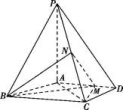
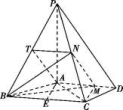
13.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(1)证明MN∥平面PAB;

(2)求四面体N-BCM的体积.

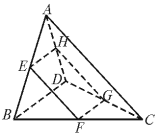
14.如图，□EFGH的四个顶点分别在空间四边形ABCD的边AB、BC、CD、DA上，求证：BD∥面EFGH，AC∥面EFGH．

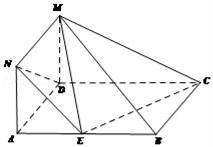
15.如图，正方形ADMN与矩形ABCD所在平面互相垂直 AB=6，AD=3

（Ⅰ）若点E是AB的中点，求证：BM∥平面NDE；

（Ⅱ）若BE=2EA，求三棱锥M﹣DEN的体积.

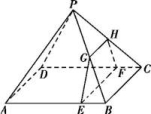
16.如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.

(1)证明:GH∥EF.

(2)若EB=2,求四边形GEFH的面积.

答案解析

1.D

2.C；

3.D；

4.B；

5.B；

6.A；

7.答案：B

解题思路：

8.A；

9.无数　无数

10.无数

11.既不充分也不必要

12.平行或异面

13.解析：(1)证明:由已知得AM=AD=2,取BP的中点T,连接AT,TN,

由N为PC中点知TN∥BC,TN=BC=2.

又AD∥BC,故TN?AM,故四边形AMNT为平行四边形,于是MN∥AT.

因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.

(2)因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为PA.

取BC的中点E,连接AE.由AB=AC=3得AE⊥BC,AE==.

由AM∥BC得M到BC的距离为,故S△BCM=×4×=2.所以四面体N-BCM的体积VN-BCM=·S△BCM·=.

14.证明：EFGH是平行四边形

BD∥面EFGH，

同理可证AC∥面EFGH．

15.

16.解析　(1)证明:因为BC∥平面GEFH,BC⊂平面PBC,且平面PBC∩平面GEFH=GH,

所以GH∥BC.同理可证EF∥BC,因此GH∥EF.

(2)连接AC,BD交于点O,BD交EF于点K,连接OP,GK.

因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.

又BD∩AC=O,且AC,BD都在底面内,所以PO⊥底面ABCD.又因为平面GEFH⊥平面ABCD,且PO⊄平面GEFH,

所以PO∥平面GEFH.因为平面PBD∩平面GEFH=GK,所以PO∥GK,则GK⊥底面ABCD,

从而GK⊥EF.所以GK是梯形GEFH的高.由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,

从而KB=DB=OB,即K为OB的中点.

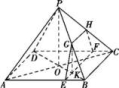
再由PO∥GK得GK=PO,即G是PB的中点,则GH=BC=4.

由已知可得OB=4,PO===6,所以GK=3.

故四边形GEFH的面积S=·GK=×3=18.