高考数学一轮复习作业本6.1 不等式的性质及一元二次不等式（含答案）

这是一份高考数学一轮复习作业本6.1 不等式的性质及一元二次不等式（含答案），共6页。
2020高考数学(理数)复习作业本6.1 不等式的性质及一元二次不等式一         、选择题1.不等式ax2+bx+2>0的解集是(-,),则a+b的值是(　   　)A.10                                        B.-10                                        C.14                                       D.-14 2.若0＜m＜1，则不等式(x－m)(x－)＜0的解集为(　　)A.{x|＜x＜m}          B.{x|x＞或x＜m}C.{x|x＞m或x＜}      D.{x|m＜x＜} 3.设集合M={x|0≤x＜2}，N={x|x2－2x－3＜0}，则有M∩N=(　　)A.{x|0≤x＜1}　　    B.{x|0≤x＜2}    C.{x|0≤x≤1}        D.{x|0≤x≤2} 4.若m<0,n>0且m+n<0,则下列不等式成立的是(　    　)A.-n<m<n<-m                  B.-n<m<-m<n        C.m<-n<-m<n                      D.m<-n<n<-m 5.若0<t<1，则不等式(x-t)(x-)<0的解集为(　　)A.{x|<x<t}　      B.{x|x>或x<t}    C.{x|x<或x>t}      D.{x|t<x<} 6.设a,b是实数,则“a>b>1”是“a+>b+”的(　　    )A.充分不必要条件                         B.必要不充分条件C.充要条件                                             D.既不充分又不必要条件 7.若角α,β满足-<α<β<π,则α-β的取值范围是(　    　)A.(-,)                    B.(-,0)        C.(0,)                    D.(-,0) 8.若不等式x2+ax-2>0在区间[1,5]上有解,则a的取值范围是(　  　)A.(-4.6，+∞)                                    B.[-4.6,1]         C.(1,+∞)                                    D.(-∞,4.6] 二         、填空题9.若a,b∈R且a>b,则下面三个不等式:①>; ②(a+1)2>(b+1)2; ③(a-1)2>(b-1)2. 其中不成立的是　　　　.(填序号)  10.若关于x的不等式的解集为(-∞，-1)∪(4，＋∞)，则实数a=________ 11.在R上定义运算:=ad-bc.若不等式≥1对任意实数x恒成立,则实数a的最大值为　　　　.  12.如果关于x的不等式5x2-a≤0的正整数解是1,2,3,4,那么实数a的取值范围是　　　　.  三         、解答题13.已知a≠0,b≠0,且a+b>0,试比较+与+的大小.            14.解不等式：(x2－x－1)(x2－x＋1)>0；                  15.设f(x)=(m+1)x2﹣mx+m﹣1.                                          (1)当m=1时，求不等式f(x)＞0的解集；                                          (2)若不等式f(x)+1＞0的解集为(1.5,3)，求m的值.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   16.已知函数f(x)=的定义域为R.(1)求a的取值范围;(2)若函数f(x)的最小值为,解关于x的不等式x2-x-a2-a<0.        
答案解析1.答案为：D；解析：由题意知-和是方程ax2+bx+2=0的两个根,则解得a=-12,b=-2,所以a+b=-14.2.答案为：D； 3.答案为：B；4.答案为：D；解析：解法一:(取特殊值法)令m=-3,n=2,分别对各选项进行检验即可.解法二:m+n<0⇒又由于m<0<n,故m<-n<n<-m成立.5.答案为：D；6.答案为：A；解析：因为,若a>b>1,显然>0,则充分性成立,当a=,b=时,显然不等式a+>b+成立,但a>b>1不成立,所以必要性不成立.故选A.7.答案为：B；解析：∵-<β<π,∴-π<-β<,又∵-<α<π,∴-<α-β<.又∵α<β,∴α-β<0,从而-<α-β<0.8.答案为：A；解析：由Δ=a2+8>0知,方程x2+ax-2=0恒有两个不等实根,又知两根之积为负,所以方程必有一正根、一负根.于是不等式在区间[1,5]上有解的充要条件是f(5)>0,即25+5a-2>0,解得a>-4.6,故a的取值范围为(-4.6,+∞). 一         、填空题9.答案为：①②③；解析：取a=,b=-3,则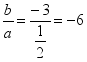,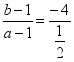=8,故①不成立,取a=-3,b=-4,则②③均不成立.故答案为①②③.10.答案为：4；11.答案为：1.5；解析：原不等式等价于x(x-1)-(a-2)(a+1)≥1,则问题转化为x2-x-1≥(a+1)(a-2)对任意x恒成立,x2-x-1=(x-)2-≥-,所以-≥a2-a-2,解得-≤a≤.则实数a的最大值为.12.答案为：[80,125)；解析：由题意知a>0,由5x2-a≤0,得-≤x≤,又正整数解是1,2,3,4,则4≤<5,∴80≤a<125. 二         、解答题13.解：.∵a+b>0,(a-b)2≥0,a2b2>0,∴≥0.∴+≥+.14.解： 15.解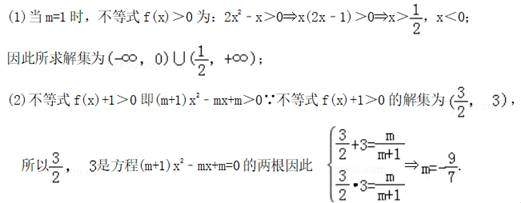：                                                                                    16.解：(1)∵函数f(x)=的定义域为R,∴ax2+2ax+1≥0恒成立,当a=0时,1≥0恒成立.当a≠0时,要满足题意,则有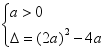解得0<a≤1.综上可知,a的取值范围是[0,1].(2)f(x)==,由题意及(1)可知0<a≤1,∴当x=-1时, f(x)min=,由题意得,=,∴a=,∴不等式x2-x-a2-a<0可化为x2-x-<0.解得-<x<,∴不等式的解集为(-,).