初中数学华师大版八年级下册18.2 平行四边形的判定作业课件ppt

这是一份初中数学华师大版八年级下册18.2 平行四边形的判定作业课件ppt，共21页。PPT课件主要包含了平行于或∥等内容，欢迎下载使用。

1. 下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是(　　 )　　　　　 　　　　　　　　　　A.1∶2∶3∶4B.2∶2∶3∶3C.2∶3∶2∶3D.2∶3∶3∶2
知识点1 两组对边分别平行的四边形是平行四边形
1.C　已知四边形的内角和为360°,当∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 时,∠A=36°,∠B=72°,∠C=108°,∠D=144°,∴∠A+∠B=108°,∠C+∠B=180°,∴AB∥CD,不能得到AD∥BC,∴不能判定四边形ABCD是平行四边形,故选项A不符合题意;同理得选项B,D不符合题意;当∠A∶∠B∶∠C∶∠D= 2∶3∶2∶3时,∠A=∠C=72°,∠B=∠D=108°,∴∠A+∠B=180°,∠C+∠B=180°,∴AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,故选项C符合题意.
2. 原创题 如图,木棒a平行于木棒b,当木棒c　　　　木棒d时,木棒a,b,c,d围成的四边形是平行四边形. 
3. 已知四边形ABCD的对角线为AC,BD,下列条件中能判定四边形ABCD是平行四边形的是 (　　)A.AB=AD,AD=BCB.AB=BC,AD=CDC.AB=CD,AD=BCD.AB=CD,AC=BD
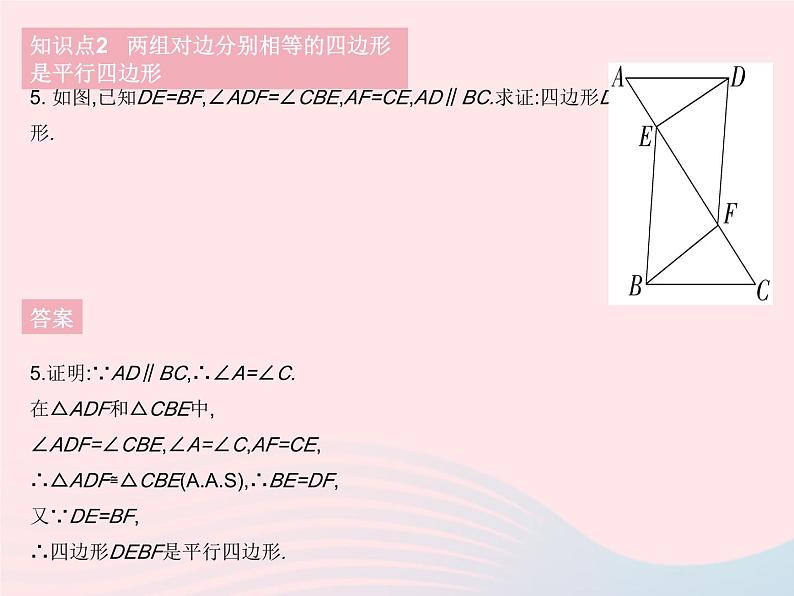
知识点2 两组对边分别相等的四边形是平行四边形
4. 如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是　　　　　　　　 　　　　　　　. 
4.两组对边分别相等的四边形是平行四边形
5. 如图,已知DE=BF,∠ADF=∠CBE,AF=CE,AD∥BC.求证:四边形DEBF是平行四边形.
5.证明:∵AD∥BC,∴∠A=∠C.在△ADF和△CBE中,∠ADF=∠CBE,∠A=∠C,AF=CE,∴△ADF≌△CBE(A.A.S),∴BE=DF,又∵DE=BF,∴四边形DEBF是平行四边形.
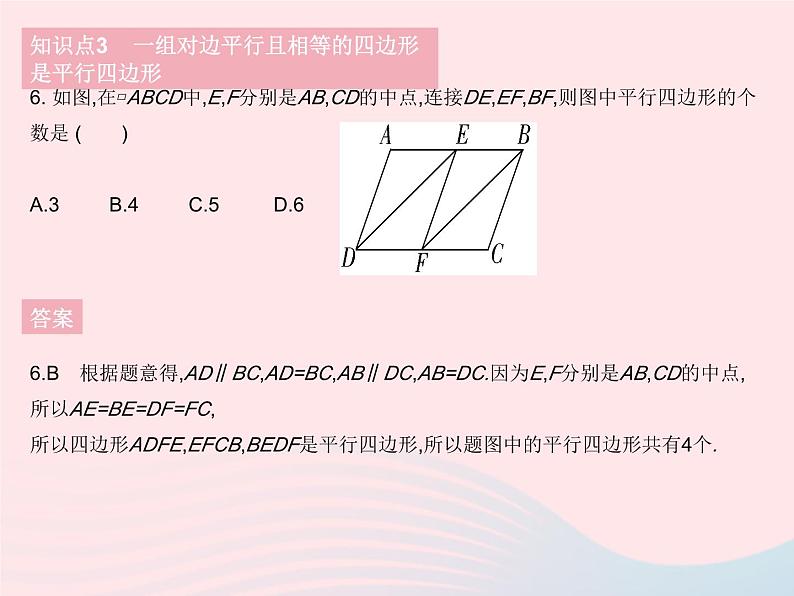
6. 如图,在▱ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,则图中平行四边形的个数是 (　　)　　　　　　　　　　　　　　　　A.3B.4C.5 D.6
知识点3 一组对边平行且相等的四边形是平行四边形
6.B　根据题意得,AD∥BC,AD=BC,AB∥DC,AB=DC.因为E,F分别是AB,CD的中点,所以AE=BE=DF=FC,所以四边形ADFE,EFCB,BEDF是平行四边形,所以题图中的平行四边形共有4个.
7. [2021黑龙江牡丹江中考]如图,在四边形ABCD中,AB=DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为　　　　. 
7.AB∥DC(或AD=BC)
8. [2021湖南郴州中考]如图,四边形ABCD中,AB=DC,将对角线AC向两端分别延长至点E,F,使AE=CF,连接BE,DF.若BE=DF,证明:四边形ABCD是平行四边形.
8.证明:在△BEA和△DFC中,AB=CD,AE=CF,BE=DF,∴△BEA≌△DFC(SSS),∴∠EAB=∠FCD,∴∠BAC=∠DCA,∴AB∥DC,又∵AB=DC,∴四边形ABCD是平行四边形.
1. [2020江苏南通期末]如图,下列条件不一定能判定四边形ABCD是平行四边形的是 (　　)A.∠A=∠C,∠B=∠DB.AB∥CD,AD∥BCC.AB∥CD,AD=BCD.AB=CD,AD=BC
2. 将△ABC(如图)绕AC边的中点O旋转180°后与原三角形拼成的四边形一定是　　　　. 
2.平行四边形　将△ABC绕AC边的中点O旋转180°后得到的三角形与原三角形是全等的,所以拼成的四边形的两组对边分别相等,所以该四边形一定是平行四边形.
3. 易错题 如图,在等边三角形ABC中,BC=6 cm,射线AO∥BC,点E从点A出发沿射线AO以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,设运动时间为t s,那么当t=　　　　时,以A,C,E,F为顶点的四边形是平行四边形. 
3.2或6　①当点F在点C的左侧时, AE=t cm,BF=2t cm,则CF=BC-BF=(6-2t)cm.∵AO∥BC,∴当AE=CF时,四边形AECF是平行四边形,此时t=6-2t,解得t=2.②当点F在点C的右侧时, AE=t cm,BF=2t cm,则CF=BF-BC=(2t-6)cm.∵AO∥BC,∴当AE=CF时,四边形AEFC是平行四边形,此时t=2t-6,解得t=6.综上可得当t=2或6时,以A,C,E,F为顶点的四边形是平行四边形.
4. 在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图(图1)的启发,编写了下面这道题,请你来解一解.如图2所示,将平行四边形ABCD的边DA,AB,BC,CD分别延长至E,F,G,H,使得AE=CG,BF=DH,连接EF,FG,GH,HE.求证:四边形EFGH为平行四边形.
4.证明:∵四边形ABCD是平行四边形,∴AB=CD,∠BCD=∠BAD.∵∠HCG=180°-∠BCD,∠EAF=180°-∠BAD,∴∠HCG=∠EAF.∵BF=DH,AB=CD,∴AF=CH,又∵AE=CG,∠FAE=∠HCG,∴△FAE≌△HCG,∴EF=GH.同理可得EH=GF,∴四边形EFGH为平行四边形.
5. 如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,连接ED,CF,AE,AD,∠EAD=60°.求证:(1)△ABE≌△ACD;(2)四边形EFCD是平行四边形.
5.证明:(1)∵△ABC和△BEF都是等边三角形,∴AB=AC,∠EBF=∠ACB=∠BAC=60°.∵∠EAD=60°,∴∠EAD=∠BAC,∴∠EAB=∠DAC.在△ABE和△ACD中,∠EBA=∠DCA,AB=AC,∠EAB=∠DAC,∴△ABE≌△ACD.(2)由(1)得△ABE≌△ACD,∴BE=CD,又∵△BEF与△ABC都是等边三角形,∴EF=BE=CD,∠EFB=∠ABC=60°,∴EF∥CD,∴EF=CD且EF∥CD,∴四边形EFCD是平行四边形.
素养提升6. 如图是以BC为底边的等腰三角形ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BF=BE.(1)求证:四边形BDEF为平行四边形.(2)当∠C=45°,BD=2时,求D,F两点间的距离.
6.(1)证明:∵△ABC是等腰三角形,∴∠ABC=∠C.∵EG∥BC,DE∥AC,∴∠AEG=∠ABC=∠C,四边形CDEG是平行四边形,∴∠DEG=∠C.∵BE=BF,∴∠F=∠BEF=∠AEG=∠ABC,∴∠F=∠DEG,∴BF∥DE,又∵EF∥BD,∴四边形BDEF为平行四边形.