第4章实数复习课件-(苏科版)

这是一份第4章实数复习课件-(苏科版)，共21页。

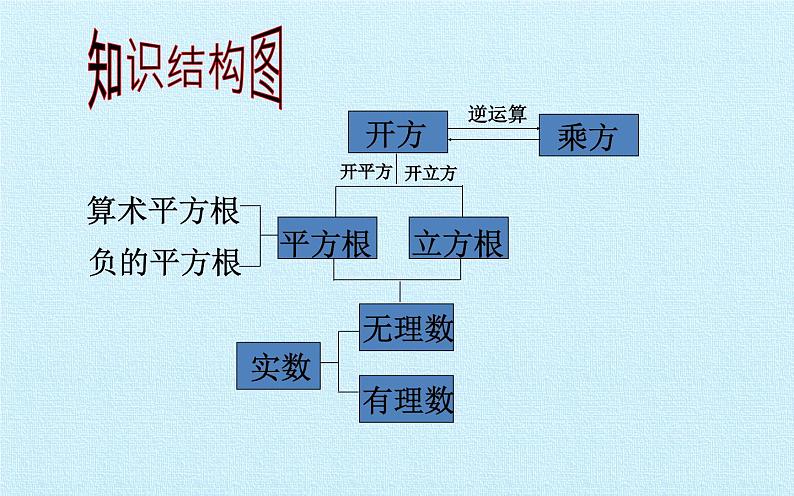
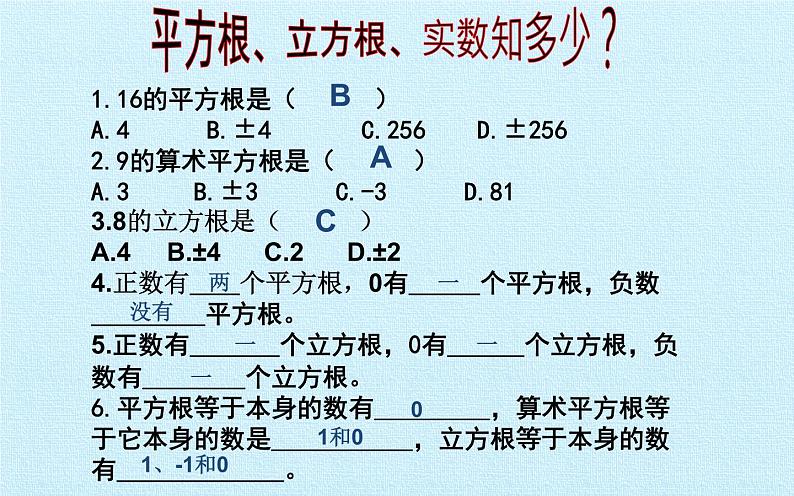
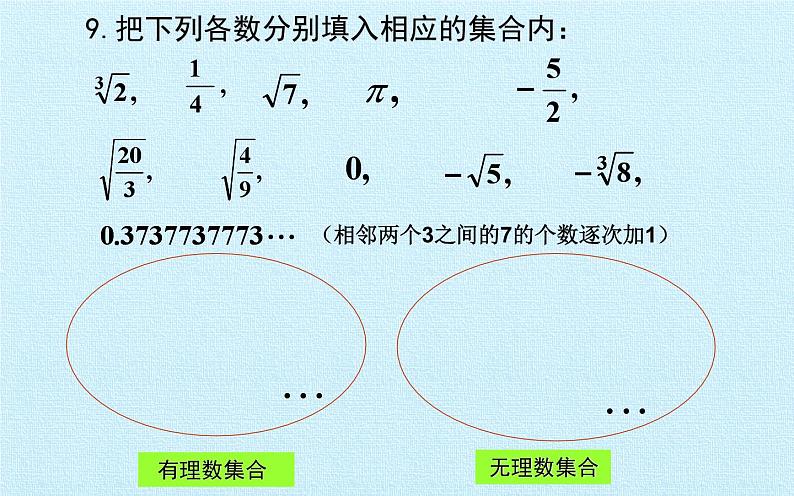
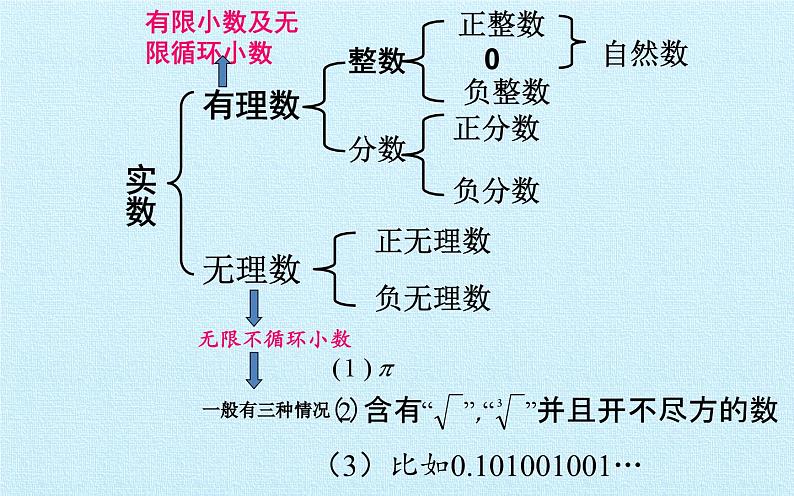
第4章 实数 复习课件算术平方根负的平方根知识结构图1.16的平方根是（　　　）A.4 B.±4 C.256 D.±2562.9的算术平方根是（　　　）A.3 B.±3 C.-3 D.813.8的立方根是（　　　）A.4 B.±4 C.2 D.±24.正数有 个平方根，0有 个平方根，负数 平方根。5.正数有 个立方根，0有 个立方根，负数有 个立方根。6.平方根等于本身的数有 ，算术平方根等于它本身的数是 ，立方根等于本身的数有 。平方根、立方根、实数知多少？BAC两一没有一一一01和01、-1和07.填空： = ; = ; = ; = ; = ; = ; = ; = ;30.5234-5±1±1/28.判断下列说法是否正确：（1）实数不是有理数就是无理数（ ）（2）无限小数都是无理数（ ）（3）无理数都是无限小数（ ）（4）带根号的数都是无理数（ ） （5）两个无理数之和一定是无理数（ ）（6）所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数（ ）（相邻两个3之间的7的个数逐次加1） 有理数集合 无理数集合9.把下列各数分别填入相应的集合内：实数有理数无理数分数整数正整数 0负整数正分数负分数自然数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况（3）比如0.101001001…1.与数轴上的点一一对应的数是（ ）A.有理数 B.无理数 C.实数 D.整数4. 最小值是 ，此时a的取值是 。 3.如果一个数的平方根是-3，那么它的另一个平方根是 。 CB32－1题组训练5.近似数3.5万精确到 位，近似数0.4062精确到 位，0.43万精确到千位为 .6.由四舍五入法得到的近似数为8.01×104，精确到（ 　） A.万位 　　　　 B.百分位 　　 C.万分位 　　　 D.百位例1：如果一个正数的平方根为a+1和 2a-7，求这个数。解：由题意得：（a+1）+（2a－7）＝0解得a＝2所以a+1＝3，2a－7＝－3所以这个数是9典例分析举一反三1、已知2a－1的平方根是±3，b+1的算术平方根是2，则a=　　，b= 。　　　2、已知x－1的平方根是±4，x+y－1的立方根是２，则x=　　，y= 。53 17－8具有双重非负性算术平方根1）被开方数 a 是非负数，即 a ≥ 0 2）算术平方根本身是非负数，即例2：已知 与 互为相反数，求（x－2y）2的平方根。解：因为 与 互为相反数所以 + =0所以 x-y+3=0 x=-1 x+y-1=0 解得 y=2 所以（x－2y）2=25， （x－2y）2的平方根是±5典例分析1、已知 ，求 的值 ；2、已知 ，求2x+y的立方根。解（1）由题意得 b-2c-1 =0 b=5 c-2=0 解得 c=2所以b+2c=9所以 =3解（2）由题意得 2x-y=0 x=2 x-2=0 解得 y=4所以2x+y=8所以2x+y的立方根是2拓展提高例3：求下面各式中的x的值（1）（x-1）2=4 （2）3（x-3）3-24=0解：（1）x-1=±2x-1=2或x-1=-2x=3或-1解：（2）3（x-3）3=24（x-3）3=8x－3=2x=5整体思想、转化思想、分类思想典例分析学以致用1.小明家客厅里5块正方形地砖的面积为32000cm2，求每一块正方形地砖的边长。2.一块直角三角形的花坛，它的两条直角边c长分别为5m，12m，求它的斜边长。课堂聚焦今日事，今日毕交流学习心得，体会丰收喜悦 平方根、立方根、实数 数学思想： 分类思想、方程思想、数形结合思想及转化思想。小结 登高才能望远，才能看到最美的风景；探索才有收获，才能感受到真正的快乐！ 愿同学们能够把握知识命脉成为一个快乐的探索者。！祝：同学们学习进步， 天天　　　　　开心！1.已知a、b满足b = 　 则a= ，b= 。2.已知 的小数部分是a， 的小数部分是b，a= ， b= ，a+b的平方根是 。挑战自我5-4±1 = .