广西北海市2021-2022学年八年级下学期期末教学质量检测数学试卷(含解析)

这是一份广西北海市2021-2022学年八年级下学期期末教学质量检测数学试卷(含解析)，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

北海市2022年春季学期期末教学质量检测
八年级数学
一、选择题：（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求．）
1．下列图形中，是中心对称图形的是（    ）
A． B． C． D．
2．已知一个多边形的内角和是，则这个多边形是（）．
A．四边形 B．五边形 C．六边形 D．七边形
3．已知数据、-5、-1.3、π、-2，其中负数出现的频率是（    ）
A．0.4 B．0.5 C．0.6 D．0.7
4．一次函数的图象与y轴交点的坐标是（    ）
A． B． C． D．
5．如图，平分，垂直于E，，，则的面积为（    ）

A．7 B．8 C．9 D．10
6．如图，菱形的周长是20，，则对角线的长度为（    )

A．5 B． C．4 D．
7．若三角形三个内角的比为，则它的最长边与最短边的比为（    ）
A． B． C． D．
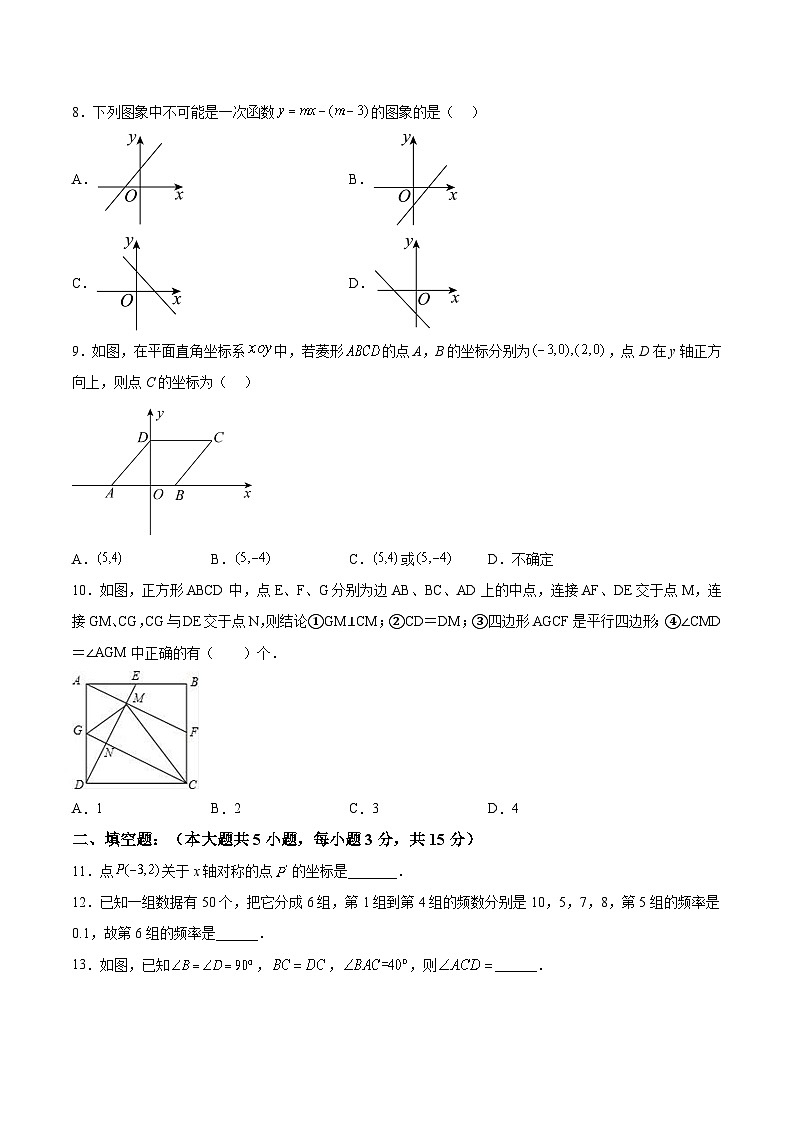
8．下列图象中不可能是一次函数的图象的是（    ）
A． B．
C． D．
9．如图，在平面直角坐标系中，若菱形的点A，B的坐标分别为，点D在y轴正方向上，则点C的坐标为（    ）

A． B． C．或 D．不确定
10．如图，正方形ABCD中，点E、F、G分别为边AB、BC、AD上的中点，连接AF、DE交于点M，连接GM、CG，CG与DE交于点N，则结论①GM⊥CM；②CD＝DM；③四边形AGCF是平行四边形；④∠CMD＝∠AGM中正确的有（　　）个．

A．1 B．2 C．3 D．4
二、填空题：（本大题共5小题，每小题3分，共15分）
11．点关于x轴对称的点的坐标是_______．
12．已知一组数据有50个，把它分成6组，第1组到第4组的频数分别是10，5，7，8，第5组的频率是0.1，故第6组的频率是______．
13．如图，已知，，，则______．

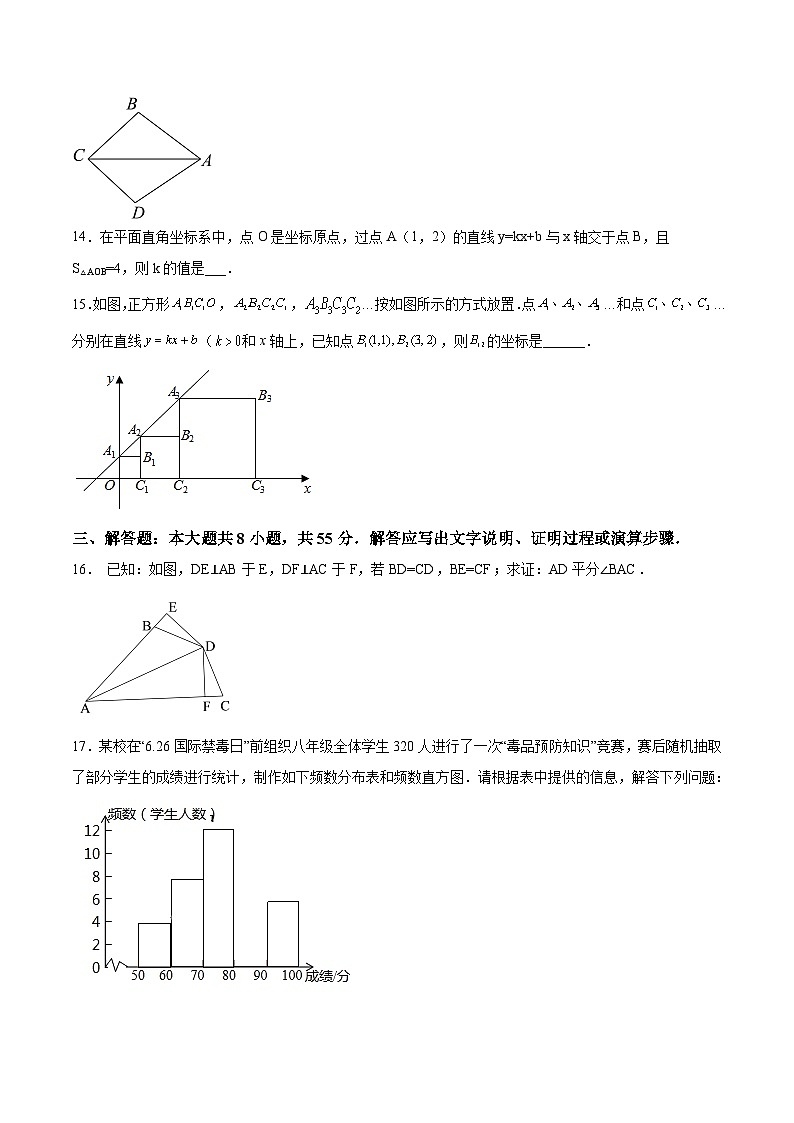
14．在平面直角坐标系中，点O是坐标原点，过点A（1，2）的直线y=kx+b与x轴交于点B，且S△AOB=4，则k的值是___．
15．如图，正方形，，…按如图所示的方式放置．点…和点…分别在直线（和x轴上，已知点，则的坐标是______．

三、解答题：本大题共8小题，共55分．解答应写出文字说明、证明过程或演算步骤．
16． 已知：如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF；求证：AD平分∠BAC．

17．某校在“6.26国际禁毒日”前组织八年级全体学生320人进行了一次“毒品预防知识”竞赛，赛后随机抽取了部分学生的成绩进行统计，制作如下频数分布表和频数直方图．请根据表中提供的信息，解答下列问题：

分数段（x表示分数）
频数
频率

4
0.10

8
b

a
0.30

10
0.25

6
0.15
(1)表中_____，_____，并补全直方图；
(2)若用扇形统计图描述此成绩统计分布表，则分数段对应扇形的圆心角度数是______．
(3)请估计该年级分数在的学生有多少人？
18． 在平面直角坐标系 中的位置如图所示，的顶点均在格点上，且点的坐标是．
（1）直接写出点和点的坐标；
（2）把 向上平移 个单位，再向右移 个单位得到，画出，并写出点的坐标．

19．一艘船以40km/s的速度向正东航行，在A处测得灯塔C在北偏东60°方向上继续航行1h．到达B处，这时测得灯塔C在北偏东30°方向上，已知在灯塔C的四周30 km内有暗礁，问这船继续向东航行是否安全？

20．如图，等腰中，，交于D点，E点是的中点，分别过D、E两点作线段的垂线，垂足分别为G、F两点．

(1)求证：四边形为矩形；
(2)若，，求的长．
21．抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利120元，销售一箱B型口罩可获利140元．该药店计划一次购进两种型号的口罩共100箱，其中B型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这100箱口罩的销售总利润为y元．
(1)求y与x的函数关系式；
(2)该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？
(3)若限定该药店最多购进A型口罩70箱，则这100箱口罩的销售总利润能否为12500元？请说明理由．
22．已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在DC边所在直线上，且随着点P的运动而运动，PE=PD总成立．
(1)如图(1),当点P在对角线AC上时,请你通过测量、观察,猜想PE与PB有怎样的关系?(直接写出结论不必证明)；
(2)如图(2),当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立，请给出证明；如果不成立，请说明理由；
(3)如图(3),当点P运动到CA的反向延长线上时,请你利用图(3)画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)

23．当m，n是非零实数，且满足时，就称点为“完美点”．

(1)若点M为“完美点”，且横坐标为2，则点M的纵坐标为________；
(2)“完美点”P在直线________（填直线解析式）上；
(3)如图，已知点，直线上的“完美点”为点E．连接，．
①求的面积；
②在平面直角坐标系中，是否存在点F，使得以点B，C，E，F为顶点的四边形是平行四边形，如果存在，请求出点F的坐标；如果不存在，请说明理由．
答案
1．D
A.不是中心对称图形，故不符合题意；
B.是轴对称图形，不是中心对称图形，故不符合题意；
C.是旋转对称图形，不是中心对称图形，故不符合题意；
D.是中心对称图形，符合题意；
故选D.
2．B
根据多边形内角和定理，n边形的内角和公式为，因此，
由
得n=5．
故选B．
3．C
解：∵在、-5、-1.3、π、-2中，负数有3个，
∴负数出现的频率是=0.6，
故选：C．
4．B
解：当x=0时，y=0+3=3，
∴图象与y轴交点的坐标是．
故选B．
5．C
解：如图，过点D作DF⊥BA交BA延长于F，

∵平分，垂直于E，DF⊥BA交BA延长于F，
∴DF=DE=3，
∴S△ABD==×6×3=9，
故选：C．
6．A
解：∵四边形ABCD是菱形，且其周长为20，
∴AB=AD=5．
∵∠A=60°，
∴△ABD是等边三角形，
∴AB=AD=BD=5．
故选：A．
7．B
解：根据题意，设三个内角分别是k，2k，3k，则k+2k+3k=180°，解得k=30°，
∴这个三角形的三个内角分别是30°，60°，90°
∴它的最长边与最短边之比为2：1．
故答案是B．
8．D
解：A、由函数图象可知，解得0＜m＜3；
B、由函数图象可知，解得m>3；
C、由函数图象可知，解得m＜0；
D、由函数图象可知，解得m＜0，m＞3，无解．
故选：D．
9．A
解：∵菱形ABCD的顶点A，B的坐标分别为（-3，0），（2，0），点D在y轴上，
∴AB=AO+OB=5，
∴AD=AB=CD=5，
∴DO==4，
∴点C的坐标是：（5，4）．
故选：A．
10．B
解：正方形ABCD中，AD=BC
∵点E、F、分别为边AB、BC上的中点，
∴AG∥FC且AG＝FC，
∴四边形AGCF为平行四边形，故③正确；
∴AF//CG
∴∠GAF＝∠FCG＝∠DGC，∠AMN＝∠GND
在△ADE和△BAF中，
∵，
∴△ADE≌△BAF（SAS），
∴∠ADE＝∠BAF，
∵∠ADE+∠AEM＝90°
∴∠EAM+∠AEM＝90°
∴∠AME＝90°
∴∠GND＝90°
∴DE⊥CG．
∵∠AMD＝90°,G点为AD中点，
∴DG=MG, DE⊥CG．
∴CG垂直平分DM，
∴CD＝CM，
但是∠MDC不等于60°，所以
CD不等于DM故②错误；
在△GDC和△GMC中，
∵ ，

∴△GDC≌△GMC（SSS），
∴∠CDG＝∠CMG＝90°，∠MGC＝∠DGC，
∴GM⊥CM，故①正确；
∵∠CDG＝∠CMG＝90°，
∴∠MGD+∠DCM=360°-∠CDG-∠CMG=180°
∵∠AGM+∠MGD=180°，
∴∠AGM＝∠DCM，
∵CD＝CM，
∴∠CMD＝∠CDM，
在Rt△AMD中，∠AMD＝90°，
∴DM＜AD，
∴DM＜CD，
∴∠DMC≠∠DCM，
∴∠CMD≠∠AGM，故④错误．
故选B．
11．（-3，-2）
点 P(−3，2) 关于x轴对称的点 P′ 的坐标是（-3，-2），
故答案是：（-3，-2）．
12．0.3
解：第5组的频数=50×0.1=5，
∴第6组的频数=50-5-7-8-10-5=15，
15÷50=0.3．
故答案为：0.3．
13．50°
解：在Rt△ABC和Rt△ADC中，
，
∴Rt△ABC≌Rt△ADC（HL），
∴∠DAC=∠BAC=40°，
∴∠DCA=90°-40°=50°，
故答案为：50°．
14．或
解：把y=0代入y=kx+b得ax+b=0，解得，∴B点坐标为（，0）．
把A（1，2）代入y=kx+b得k+b=2，则b=2﹣k．∴B点坐标为（，0）．
∵S△AOB=4，∴|，即|或．
15．
解：∵B1的坐标为（1，1），点B2的坐标为（3，2），
∴正方形A1B1C1O1边长为1，正方形A2B2C2C1边长为2，
∴A1的坐标是（0，1），A2的坐标是：（1，2），
代入y=kx+b得：，解得：，
则直线的解析式是：y=x+1．
∵A1B1=1，点B2的坐标为（3，2），
∴点A3的坐标为（3，4），
∴A3C2=A3B3=B3C3=4，
∴点B3的坐标为（7，4），
∴B1的纵坐标是：1=20，B1的横坐标是：1=21-1，
∴B2的纵坐标是：2=21，B2的横坐标是：3=22-1，
∴B3的纵坐标是：4=22，B3的横坐标是：7=23-1，
∴Bn的纵坐标是：2n-1，横坐标是：2n-1，
则Bn（2n-1，2n-1）．
∴B12的坐标是：（212-1，211）．
故答案为：（212-1，211）．
16．证明：∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°，
在Rt△BDE和Rt△CDF中，
∴Rt△BDE≌Rt△CDF，
∴DE=DF，
又∵DE⊥AB，DF⊥AC，
∴AD平分∠BAC.
17．(1)解：∵调查的总人数是：4÷0.1=40（人）
∴a=40×0.3=12（人），
b=8÷40=0.2；
补全直方图如图所示，

故答案为：12，0.2；
(2)解：分数段对应扇形的圆心角度数是：
360°×0.2=72°；
故答案为：72°；
(3)解：320×（0.25+0.15）=128
∴估计该年级分数在80≤ x﹤100的学生有128人．
18．（1），；
（2）如图，△A1B1C1为所作，

的坐标．
19．解：过点C作CD⊥AB，垂足为D．如图所示：

根据题意可知，∠DBC=90°-30°=60°，
∵，
∴，
∴（），
在中，，，
，
∴ ，
∴这艘船继续向东航行安全．
20．（1）证明：，，
点是的中点．
点是的中点，
是的中位线．
．
，，
．
四边形是平行四边形．
又，
四边形为矩形；
（2）交于点，点是的中点， ，
．
由（1）知，四边形为矩形，则．
在直角中，，，由勾股定理得：．
，，
，
，    
．
21．（1）解：（1）根据题意得，
y＝120x＋140（100−x）＝−20x＋14000，
答：y与x的函数关系式为：y＝−20x＋14000；
（2）（2）根据题意得，100−x≤3x，解得x≥25，
∵y＝−20x＋14000，k＝−20＜0；
∴y随x的增大而减小，
∵x为正整数，
∴当x＝25时，y取最大值为−20×25＋14000＝13500，则100−x＝75，
即商店购进A型口罩25箱、B型口罩75箱，才能使销售总利润最大，最大利润为13500元；
（3）（3）根据题意得25≤x≤70，
∵y＝−20x＋14000，k＝−20＜0；
∴y随x的增大而减小，
∵x为正整数，
∴当x＝70时，y取最小值为−20×70＋14000＝12600，
∵12600＞12500，
∴这100箱口罩的销售总利润不能为12600元．
22．(1)①PE=PB，②PE⊥PB.
(2)(1)中的结论成立．
①∵四边形ABCD是正方形，AC为对角线，
∴CD=CB，∠ACD=∠ACB，
又PC=PC，
∴△PDC≌△PBC，
∴PD=PB，
∵PE=PD，
∴PE=PB，
②：由①,得△PDC≌△PBC，
∴∠PDC=∠PBC.
又∵PE=PD，
∴∠PDE=∠PED.
∴∠PDE+∠PDC=∠PEC+∠PBC=180°，
∴∠EPB=360°−(∠PEC+∠PBC+∠DCB)=90°，
∴PE⊥PB.
(3)如图所示：

结论：①PE=PB，②PE⊥PB.
23．（1）解：∵点M为“完美点”，且横坐标为2，
∴4×2-6n=3×2•n，解得n=，
∴，
故答案为：3；
（2）解：设“完美点”，
∵4m-6n=3mn，m，n是非零实数，
∴4•-6=3m，
∴，
∴P在直线上，
故答案为：；
（3）解：①设直线AB的解析式为，
把点A（3，0），B（0，4）分别代入，得
，解得，
∴直线AB的解析式为：y＝−x+4，
由（2）知“完美点”E在直线上，
联立
解得，
∴E，
∴△CBE的面积=．
②当EFBC且EF=BC时，点B，C，E，F为顶点的四边形是平行四边形，如图1，

则，则F的纵坐标为，即或，
此时F坐标为或
当CFBE,CE BF时，点B，C，E，F为顶点的四边形是平行四边形，如图2，

∵直线AB的解析式为，
∴平行于直线AB且过点C的直线是，
由（2）知“完美点”E在直线上，且 ，
∴直线EC解析式为，
∴平行于直线EC且过点B的直线是，
联立方程组，得，解得  ，
此时F的坐标为 ，
综上，F的坐标为或或 ，