数学人教版21.1 一元二次方程教案

第二章   一元二次方程

2.5一元二次方程的根与系数的关系

教学目标：

知识技能目标

1.能说出根与系数的关系；

2.会利用根与系数的关系解有关的问题.

过程性目标

在经历观察、归纳、猜想、验证的这个探索发现过程中，通过尝试与交流，开拓思路，体会应用自己探索成果的喜悦.

情感态度目标

1.通过观察、实践、讨论等活动，经历发现问题，发现关系的过程，养成独立思考的习惯；

2.通过交流互动，逐步养成合作的意识及严谨的治学精神.

重点和难点：

重点：一元二次方程两根之和，及两根之积与原方程系数之间的关系；

难点：对根与系数这一性质进行应用.

教学过程：

一、创设情境

1．请说出解一元二次方程的四种解法.

2．解下列方程，将得到的解填入下面的表格中，你发现表格中两个解的和与积和原来的方程有什么联系？

(1)x2－2x＝0；

(2)x2＋3x－4＝0；

(3)x2－5x＋6＝0.

让学生先解出方程的正确答案，再观察两解的和、积与原方程中的系数的关系，并加以证明.

二、探究归纳

可以得到；两个解的和等于一次项系数的相反数，两个解的积等于常数项.

一般地，对于关于x的方程x2＋px＋q＝0（p，q为已知常数，p2－4q一般地，对于关于x的方程x2＋px＋q＝0（p，q为已知常数，p2－4q≥0），试用求根公式求出它的两个解x1、x2，算一算x1＋x2、x1•x2的值，你能得出什么结果？与上面发现的现象是否一致.

（此探索过程让学生分组进行交流、协作完成）

探索过程

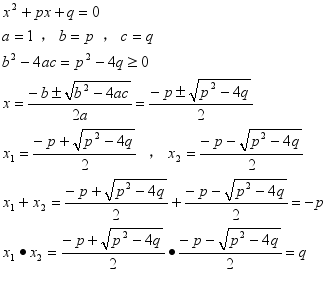
结论：两根之和等于一次项系数的相反数，两根之积等于常数项，这与上面的发现是一致的.

三、实践应用

例 1 已知关于x的方程x2－px＋q＝0的两个根是0和－3，求p和 q的值.

解法一：因为关于x的方程x2－px＋q＝0的两个根是0和－3，所以有

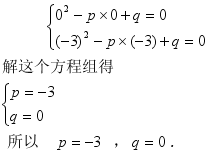
解法二：由，

方程x2－px＋q＝0的两个根是0和－3，可得

例2 写出下列方程的两根和与两根积：

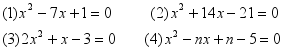
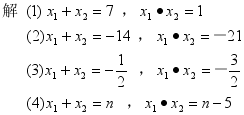
课堂练习

1.写出下列方程的两根和与两根积：

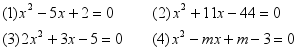
2.已知关于x的方程x2－6x＋p2－2p＋5＝0的一个根是2，求方程的另一个根和p的值.

四、交流反思

1.通过这节课的学习，掌握探索的步骤：观察——归纳——猜想——证明；

2.通过本节课探索出一元二次方程的根与系数的关系.

五、检测反馈

1.已知关于x的方程x2－2x＋m2+m－2＝0的一个根是2，求方程的另一个根和m的值.

2.写出下列方程的两根和与两根积：

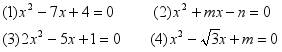
3.已知关于x的方程2x2－mx－m2＝0有一个根是1，求m的值.

六、布置作业

习题2.8