

人教版九年级上册24.2.2 直线和圆的位置关系公开课第1课时教学设计
展开24.2.2 直线和圆位置关系教案
一、【教材分析】
教
学
目
标
知识
技能
1.使学生理解直线和圆的位置关系,掌握直线和圆的位置关系的数量关系定理及其运用.
2.掌握切线的性质、判定及其应用.
过程
方法
1.通过对直线和圆的三种位置关系的直观演示,向学生渗透分类、数形结合的思想,培养学生能从直观演示中归纳出几何性质的能力.
2.初步培养学生能将点和圆的位置关系和点到圆心的距离的数量关系互相对应的理论迁移到直线和圆的位置关系上来.
3.让学生通过操作实践、思考、交流探索归纳出切线的判定定理及性质定理.
情感
态度
让学生从运动的观点来观察直线和圆相交、相切、相离的关系、关注知识的生成,发展与变化的过程,主动探索,勇于发现.从而领悟世界上的一切物体都是运动变化着的,并且在一定的条件下可以转化的辩证唯物主义观点.
教学
重点
使学生正确理解直线和圆的位置关系,掌握切线的判定定理及其性质定理.
教学
难点
直线和圆的位置关系与圆心到直线的距离和圆的关径大小关系的对应,它既可做为各种位置关系的判定,又可作为性质,学生不太容易理解.切线的判定定理及其性质定理的灵活应用.
二、【教学流程】
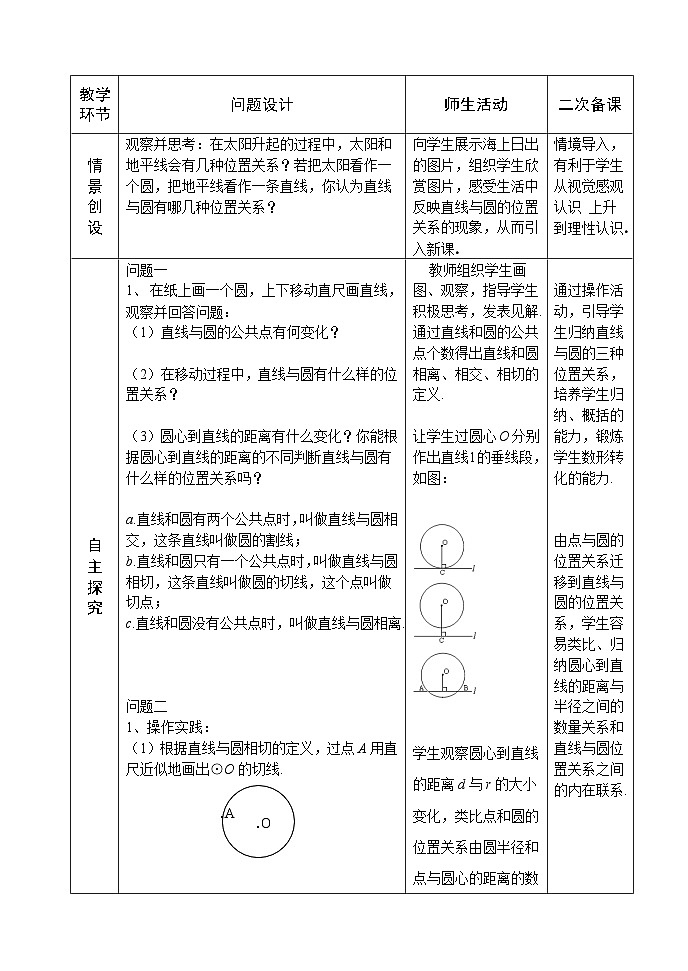
教学环节
问题设计
师生活动
二次备课
情
景
创
设
观察并思考:在太阳升起的过程中,太阳和地平线会有几种位置关系?若把太阳看作一个圆,把地平线看作一条直线,你认为直线与圆有哪几种位置关系?
向学生展示海上日出的图片,组织学生欣赏图片,感受生活中反映直线与圆的位置关系的现象,从而引入新课.
情境导入,有利于学生从视觉感观认识 上升到理性认识.
自
主
探
究
问题一
1、 在纸上画一个圆,上下移动直尺画直线,观察并回答问题:
(1)直线与圆的公共点有何变化?
(2)在移动过程中,直线与圆有什么样的位置关系?
(3)圆心到直线的距离有什么变化?你能根据圆心到直线的距离的不同判断直线与圆有什么样的位置关系吗?
a.直线和圆有两个公共点时,叫做直线与圆相交,这条直线叫做圆的割线;
b.直线和圆只有一个公共点时,叫做直线与圆相切,这条直线叫做圆的切线,这个点叫做切点;
c.直线和圆没有公共点时,叫做直线与圆相离.
问题二
1、操作实践:
.O
.A
(1)根据直线与圆相切的定义,过点A用直尺近似地画出⊙O的切线.
(2)圆的直径是13cm,如果直线与圆心的距离分别是①4.5cm②6.5cm③8cm,那么直线和圆分别是什么位置关系?有几个公共点?
.O
.A
2、思考:如图在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线的距离是多少?直线l和⊙O有什么位置关系?
直线与圆相切 d=r ;
直线与圆相离 d>r;
直线与圆相交 d
3、思考:将第2题反过来,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?
圆的切线垂直于经过切点的半径.(教师板书)
教师组织学生画图、观察,指导学生积极思考,发表见解.
通过直线和圆的公共点个数得出直线和圆相离、相交、相切的定义.
让学生过圆心O分别作出直线l的垂线段,如图:
学生观察圆心到直线的距离d与r的大小变化,类比点和圆的位置关系由圆半径和点与圆心的距离的数量关系来判定,讨论、概括、总结得出直线与圆的位置关系由圆心到直线的距离与圆半径之间的数量关系:
学生根据直线与圆相切的定义,有且只有一个公共点,近似地画出⊙O的切线.
学生应用上面的结论,独立完成问题(2),为下面第2题的思考作铺垫.
结合第1题的操作实践,学生交流探索,可以看出,这时圆心O到直线l的距离就是⊙O的半径,由前面的结论可以得出:直线l是⊙O的切线.这样,我们得到切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.(教师板书)
学生先进行猜想,得到结论:
然后教师引导学生利用反证法给出性质定理的证明,体验性质定理与判定定理的联系与区别.
通过操作活动,引导学生归纳直线与圆的三种位置关系,培养学生归纳、概括的能力,锻炼学生数形转化的能力.
由点与圆的位置关系迁移到直线与圆的位置关系,学生容易类比、归纳圆心到直线的距离与半径之间的数量关系和直线与圆位置关系之间的内在联系.
由思考出发,引导学生探索问题的解决办法,理解切线识别的必要条件.
利用反证法证明,再次熟悉反证法的使用方法,体会反证法证明的优越性.
尝
试
应
用
1、已知圆的直径为12cm,如果直线和圆心的距离为 ⑴ 5.5cm; ⑵ 6cm; ⑶ 8cm 那么直线和圆有几个公共点?为什么?
2、已知圆的直径为13cm,圆心到直线ι的距离为6cm,那么直线ι和这个圆的公共点的个数是 .
3. 已知⊙O的直径为6,P为直线ι上一点,OP=3,那么直线与⊙O的位置关系是__________.
4、在中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何位置关系?为什么?(1)r=2cm;(2)r=2.4cm;(3)r=3cm.
5、课本第96页练习第1、2题
教师出示题目,学生独立思考、解答. 学生解答完毕后,小组交流后以小组为单位展示小组的成果.
教师巡视,帮助学习有困难的学生,并适时指导、点拨,不断提升、总结
对于第4题,师生共同分析,学生自主完成,老师指导学生规范解题过程.
通过问题的训练,加深学生从多个角度对所学知识加以运用,理解直线与圆的三种位置关系.
通过第4题的教学,不仅要让学生理解它的判定方法,还应掌握如何运用该判定方法判断直线与圆的位置关系,促进学生解题能力的提高.活学活用
补
偿
提
高
1、已知Rt△ABC的斜边AB=8,AC=4,以点C为圆心作圆,当半径R=_____时,AB与⊙C相切.
2、已知OA平分∠BOC,P为OA上任意一点,如果以P为圆心的圆与OC相离,那么⊙P与OB的位置关系是( )
A. 相离 B. 相切
C. 相交 D. 不能确定
3、习题24.2第101页第4题
4、东海某小岛上有一灯塔A,已知A塔附近方圆25海里范围内有暗礁,我110舰在O点处测得A塔在其北偏西60°方向,向正西方向航行20海里到达B处,测得A在其西北方向.如果该舰继续航行,是否有触礁的危险?请说明理由.(提示=1.414,=1.732)
教师出示题目,学生有针对性的进行思考、解答.教师巡视,检查了解学生的掌握情况.
学生尝试正确画出图形,讨论、试解,看清条件与图形做出正确的判断
加深学生理解用d与r的数量关系判断直线与圆的位置关系.
小
结
作
业
小结:
通过这节课的学习,你有什么收获?
作业:
1.必做题
教材习题24.2P101第2题, P102第12题
2、 选做题
如图,直角梯形ABCD中,∠A=∠B=90°,AD//BC,E为AB上一点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与边DC有怎样的位置关系?为什么?(提示:过E作EF⊥CD于F,证点E是以AB为直径的圆的圆心)
教师提出问题,学生独立回答,教师在学生总结后进行补充,并根据学生的回答,结合结构图总结本节知识.
教师布置作业,动员分层要求.学生按要求课外完成,通过课后作业巩固本节知识.
供学生课后探讨、研究
使学生能够回顾、总结、梳理所学知识.培养学生反思自己学习过程的意识,充分发挥学生的主体作用,从而培养归纳、表达的能力.
三、【板书设计】
24.2.2 直线和圆的位置关系
.O
.A
直线与圆相切 d=r ;
直线与圆相离 d>r;
直线与圆相交 d
四、【教后反思】
本节在学习直线和圆的位置关系时,首先让学生观察海上日出的图片,再让学生画圆和直线,由交点个数不同探究平面内直线与圆有哪些位置关系.利用知识迁移规律,将点与圆位置关系中d与r的数量关系转化为直线与圆位置关系中的数量关系,从而得到直线与圆位置关系的另一种判定方法.接着学生经过操作实践、思考、交流探索得到切线的判定定理,进而又得出切线的性质定理,完成新知识体系的建构.最后通过例题练习进行实践操作,实现知识从认识到应用的转化,达到理想的教学效果.
初中数学人教版九年级上册24.2.2 直线和圆的位置关系优秀第1课时教案设计: 这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系优秀第1课时教案设计,共7页。教案主要包含了教学目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
初中数学人教版九年级上册24.2.2 直线和圆的位置关系优质课第1课时教学设计及反思: 这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系优质课第1课时教学设计及反思,共7页。教案主要包含了教学目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
人教版九年级上册24.2.2 直线和圆的位置关系第1课时教案: 这是一份人教版九年级上册24.2.2 直线和圆的位置关系第1课时教案,共4页。教案主要包含了教材分析,教学目标,教学重难点,教学过程,板书设计,教学反思等内容,欢迎下载使用。













