《等腰三角形的轴对称性》教学设计2-七年级下册数学北师大版

这是一份《等腰三角形的轴对称性》教学设计2-七年级下册数学北师大版，共4页。
        3  简单的轴对称图形                 第1课时    等腰三角形教学目标1、知识与技能目标：（1）探索并掌握等腰三角形的轴对称性及其相关性质。                  （2）经历探索简单图形轴对称的过程，进一步体验轴对称的特征，                      发展空间观念。2、过程与方法目标：通过学生的操作与思考，使学生掌握等腰三角形和等边三角形的轴对称性及其有关性质，从而发展空间观念；通过运用等腰三角形的性质解决有关的问题，培养分类讨论、方程的思想和添加辅助线解决问题的能力，发展应用意识。3、情感与态度与价值观目标：引导学生对图形的观察、发现，激发学生的好奇心和求知欲， 并在解答问题的过程中获取成功的体验，建立学习的自信心 。教学重点和难点本节课的重点是：1、使学生了解等腰三角形的有关概念。                2、通过动手操作和观察，掌握等腰三角形的轴对称性及其相关性质本节的教学难点是：1、探索等腰三角形的轴对称性及其性质的过程。                  2、等腰三角形的性质的运用 教学过程教学环节教师活动预设学生行为设计意图环节一：复习巩固观察下列各种图形，判断是不是轴对称图形,能找出对称轴吗？ 环节二、情境导入1、观察下列图片，它们有什么共同的特征？2、探究：如图所示，把一张长方形的纸按照图中虚线对折并减去阴影部分，再把它展开得到的△ABC有什么特点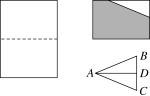？环节三、思考探究，获取新知探究1：等腰三角形1、请结合图形，指出等腰三角形的腰、底边、顶角、底角. 2、画出三种不同的等腰三角形　　通过认真观察，合作交流，能轻松地找到等腰三角形并能一一指出等腰三角形的腰、底边、顶角、底角有的学生找等腰三角形时，会疏漏等边三角形展示生活中美丽图片，让学生感知等腰三角形的对称美，唤起学生的学习兴趣和探索欲望.知道等腰三角形各元素名称，为进一步的学习和探究活动做准备.探究2：等腰三角形的性质问题：等腰三角形是轴对称图形吗？有几条对称轴？怎样找到它的对称轴？如何描述它的对称轴？  1. 做一做：要求每个同学拿出一张长方形纸，把它对折，请你通过折折、剪剪等活动，制作出一个等腰三角形.   鼓励学生充分的进行交流，探索等腰三角形的特征。 分小组活动，学生开动脑筋，既各显神通，又通力合作。通过折一折、剪一剪等方法制作出一个等腰三角形.    动手操作的形式折出等腰三角形以及对称轴，用以发现等腰三角形的轴对称性 充分调动学生思考 2. 想一想：  1  等腰三角形是轴对称图形吗？找出对称轴。  2   顶角的平分线所在的直线是等腰三角形的对称轴吗？  3   底边上的中线所在的直线是等腰三角形的对称轴吗？底边上的高呢？  4  沿对称轴折叠，你能发现等腰三角形的哪些特征？   学生独立思考、探索性质，发现等腰三角形abc这条底边上的高ad平分顶角∠a并且平分底边bc, 这条线段在等腰三角形中扮演了三种角色，从而得到等腰三角形的性质：   等腰三角形顶角的平分线、底边上的中线、底边上的高重合（也称为“三线合一”）.     探索等腰三角形的轴对称性及其有关性质，教学时，可以让学生想象等腰三角形的对称轴是什么，然后 ，通过操作验证自己的结论，并由此探索等腰三角形的有关特征。 提出问题：  等腰三角形有哪些性质？引导学生归纳小结独立思考回答，回答不完整可以有其他同学补充学生对等腰三角形的认识比较到位，培养学生的归纳能力 与学生共同探究并引导学生进行演绎推理探究3. 等边三角形  1、等边三角形的有关概念  2、你能发现等边三角形的哪些特征？探究4.你有哪些方法可以得到一个等腰三角形？与同伴交流环节四|运用新知，深化理解1  等腰三角形的一个内角是50°，则这个三角形的底角的大小是(　　)  A．65°或50°       B．80°或40°    C．65°或80°       D．50°或80° 2.填空：（1）等腰直角三角形的每一个锐角的度数是          ；（2）如果等腰三角形的底角等于40°，那么它的顶角的度数是_________ ；（3）如果等腰三角形有一个内角等于80°，那么这个三角形的最小内角等于____________ . (4)△ ABC中，AB=AC,∠A= 36◦,则∠B= ___，∠C= ____. (5)△ ABC中，AB=AC,∠B= 36◦,则∠A= ____，∠C= ____(6)△ ABC中，AB=AC,∠A= 100◦,则∠B= ___，∠C= ____.3. ⑴等腰三角形的一个角是70°，它的另外两个角的度数是                 .⑵等腰三角形的一个角是90°，它的另外两个角的度数是                   .⑶等腰三角形的一个角是110°，它的另外两个角的度数是                 .方法总结：等边对等角！4.墙上钉一根木条，怎样检验这根木条是否水平先由学生独立完成，然后进行交流 变式练习，学生自主探究.培养学生运用知识解决问题的能力5 、如图，在ΔABC中，AB=AC , 点D在AC上，且BD=BC=AD , 求∠A和∠C的度数. 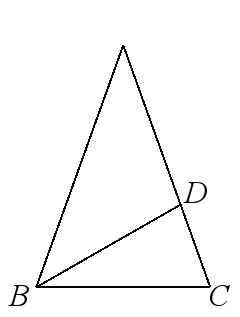   环节五课堂小结     教师在这一环节中要仔细聆听，对于学生的错误和漏洞要及时作出纠正和补充归纳整理：等腰三角形的性质，以及在习题中出现的解题方法。强调：1.“三线合一”应注意的问题：必须以等腰三角形为前提.2.“等边对等角”的前提是“在同一三角形中” 在总结中发挥学生的主体地位，让学生自己进行总结归纳   一方面通过小结对今天所学知识进行一个概括和升华，对学生易错的知识加以强调和补充；另一方面，通过教师和学生的交流，进一步激发学生的学习兴趣，鼓励学生发表自己的见解，为今后的学习打好坚实的基础。环节六：布置作业习题5.3  知识技能1，2,学生应认真独立完成作业落实本节课所学习的知识内容。板书设计（需要一直留在黑板上主板书）1、 等腰三角形的定义：2、 等腰三角形的性质1：等腰三角形的两底角相等（等边对等角）                2：等腰三角形的三线合一性质3、等腰三角形中辅助线作法：    4、运用等腰三角形性质应注意：学生学习活动评价设计教学反思     1. 学生在回答问题时表现出差异，有的学生从分析等腰三角形特点的基础上直接想象出它的对称轴，有的学生需要借助折叠等活动寻找出对称轴，但学生交流与合作不够。 今后的教学中，要鼓励学生进行充分的交流，尽可能多的探索等腰三角形的特征，尽量运用自己的语言说明理由，既可以根据折叠过程中某些线段或角重合说明，对于少数学生可以鼓励他们用全等来说明。但对于全体学生而言，只要求掌握教科书中列出的特征。     应注重操作和思考的有机结合，对于通过想象解决问题的学生，鼓励他们通过操作进行验证；对于通过操作得出结论的学生，鼓励他们重新观察等腰三角形的轴对称性。 2. 对于对称轴的描述，学生有不同的回答，有的学生回答是顶角平分线所在直线，有的学生回答是底边上的中线或高所在直线，此时应该抛出问题：“你们所说的是同一条直线吗？”引出后面两题的讨论，取得了满意的效果。  3. 本节课，对“等角对等边”的探索，由于有了前面观察和动手操作的经验，加上刚学习了三角形全等的知识，所以就增加了添加辅助线进行演绎推理的训练，注重培养了学生的逻辑思维能力。我认为是对初中数学难点的分散，教学效果还有待今后观察。