《移项解一元一次方程》教学设计2-七年级上册数学北师大版

5.2解方程

教学重点与难点

教学重点：让学生通过观察，独立归纳出移项法则，并能熟练地运用．

教学难点：移项的同时必须变号．

学情分析

在第一节的学习中，学生已经练习了如何利用等式的基本性质来解简单的一元一次方程，掌握情况较好，再加上小学阶段已具有的解方程的经验，本节让学生继续借用等式的基本性质1推导和归纳移项法则，应该不是难事．不过开始时学生可能还是会习惯性地使用逆运算，同时计算能力也有待提高．

教学目标

1．熟悉利用等式的基本性质解一元一次方程的基本过程．

2．通过具体的例子归纳移项法则．

3．利用移项法则解方程．

4．通过观察、独立思考等过程，培养学生归纳、概括的能力．

教学方法

先复习第一节所学的等式的两条基本性质，在此基础上借助分析引出方程的解答步骤，引导学生观察、归纳，独立发现移项法则，让学生明确移项的目的就是把含有未知数的项和不含未知数的项分开，从而化为ax＝b的形式，最后通过练习巩固法则并准确运用．

教学过程

一、复习导入

设计说明

本节直接用复习上节所学重点知识的方式导入新课，一是可以反馈学生对知识点的落实情况，二是其中的等式基本性质1就是新课中移项法则的理论依据，有一举两得的功效．

投影显示

1．填空：

等式的性质1：等式两边同时加上(或减去)__________，所得结果仍是__________．用字母表示为：若a＝b，则a±__________＝b±__________(__________)．

括号内填条件时应注意：所填字母表示一个代数式．

等式的性质2：等式两边同时乘以__________(或除以__________)，所得结果仍是__________．

用字母表示为：若a＝b，则a×__________＝b×__________；a÷__________＝b÷__________.

括号内填条件时应注意：所填字母表示一个非零数．

教学说明

复习题1采用填空题的形式，同时兼顾了等式两条基本性质的语言叙述与符号表示，学生掌握情况良好．复习题2是解两个简单的方程，目的是让学生实践性质的应用．操作时可以让学生先独立完成，然后在小组内由组长负责批改反馈即可．

二、讲授新课

设计说明

通过“探索练习——观察归纳——例题解析”的逻辑顺序，让学生经历自主观察发现规律并进行描述的过程，从而提升抽象问题的能力，再配合例题的讲解训练，逐步体会出移项法则的优越性．

1．探索练习

阅读解方程的过程：

解：(1)5x－2＝8，方程两边都加上2，得5x－2＋2＝8＋2，

即5x＝10，

即x＝2.

(2)7x＝6x－4，方程两边都减去6x，得7x－6x＝6x－6x－4，

即7x－6x＝－4，

即x＝－4.

2．观察归纳

问题1：分别将变化前后的两组方程进行对比，大家可以发现几处不同？(可以用下图进行演示)

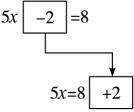
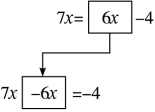
学生很容易找到：一是项的位置发生变化(从方程的一边移到了另一边)；二是项的符号发生变化(移动前后符号相反)．

问题2：你能用数学语言归纳出这个规律吗？你能说出这个规律产生的依据吗？(在学生回答的基础上，投影显示以下内容)

移项法则：将方程中的一些项改变符号后，从方程的一边移到另一边．

变形依据：等式的基本性质1.

问题3：你认为在应用法则时应该注意哪些问题呢？

学生可以从多个方面和角度去分析，但最后答案一般会集中在以下两点：

(1)所移动的是方程中的项，并且是从方程的一边移到另一边，而不是从方程的一边交换两项的位置；(2)移项时必须要变号．

随堂练习　下列变形是移项的是(　　)

A．由5＝x，得x＝5

B．由2x－3＝x＋5，得2x－x＝5＋3

C．由x＝1，得x＝2

D．由－1＝＋2，得5x－1＝＋2

答案：B

3．例题解析

例1　解下列方程：

(1)2x＋6＝1；(2)3x＋3＝2x＋7.

解：(1)移项，得2x＝1－6.

合并同类项，得2x＝－5.

方程两边同除以2，得x＝－.[

(2)移项，得3x－2x＝7－3.

合并同类项，得x＝4.

本题可以采用学生口述，教师板演的方法，因为这是解方程一节安排的第一组例题，教学时必须强调解题的规范步骤和格式，同时教师还应及时纠正学生可能出现的错误，适时组织学生交流改错．

例2　解方程：x＝－x＋3.

解：移项，得x＋x＝3.

合并同类项，得x＝3.

方程两边同除以(或同乘以)，得x＝4.

本题建议首先放手让学生去做．学生可能采取多种方法解答，教学时不应拘泥于教材提供的解法，只要合理都应该给予鼓励．

教学说明

大部分学生在归纳“移项法则”的过程中，表现出了较强的观察、总结能力，并乐意在解方程时使用这种优于小学用逆运算关系解方程的方法，理解也比较到位，基本能做到移项要变号．需要补充说明的是，还有部分学生仍习惯用逆运算，而非移项法则来解方程，对此教师不宜强求，因为法则不能只强调记忆，更应强调理解，随着后面题目的逐渐训练，让学生自己逐步体会移项的优越性．

三、变式训练，熟练技能

练习：(1)10x－3＝9；(2)5x－2＝7x＋8；(3)x＝x＋16.

答案：(1)x＝；(2)x＝－5；(3)x＝－32.

教学说明

本节课的重点是学习移项法则，所以在方程的选择上，都是移项后再合并同类项的比较简单的题目，目的在于让学生能较好的落实法则内容，并与前一节内容相比较，感受这种解法的简洁性．

四、总结反思

通过今天的学习你有哪些收获？你认为应该提醒同学注意哪些事项？

组织学生先在小组内反思讨论，然后互相补充，总结以下几点：

1．移项法则：将方程中的一些项改变符号后，从方程的一边移到另一边．

2．方法：一般把含未知数的项放在方程的左边，常数项移到方程的右边．

3．要点：(1)移项一定要变号，同时未移动的项不能变号；

(2)注意区分“移项”与“项的换序”的不同．

4．依据：等式的基本性质1.

5．目的：为了合并同类项，将方程化为ax＝b的形式．

评价与反思

1．方程是处理问题的一种很好的途径，而解方程又是这种途径必须要掌握的．教学中教师充分应用小组合作学习的优势，通过问题的引导，让学生在合作与交流中探索用移项法则解方程的一般过程与规律，并在前面探索的基础上辅助适当练习，从而理解法则的本质，构建自己的认知结构．

2．鉴于本节课的内容易于学生探索实现，所以安排了合理有效的小组活动：一是在学生进行小组合作学习时，给了学生充分独立思考的时间；二是在学生小组合作学习时，教师从讲台上来到学生中间，与学生一起参与讨论与交流；三是学生进行小组合作学习时，教师提供了适当的问题让学生充分讨论；四是学生汇报时，教师能根据学生的回答情况适时加以点拨与指导，真正实现了小组合作学习、学生的独立思考与教师的有效指导的紧密结合．