数学5.6 应用一元一次方程——追赶小明课文配套课件ppt

这是一份数学5.6 应用一元一次方程——追赶小明课文配套课件ppt，共27页。PPT课件主要包含了速度×时间，路程÷时间，路程÷速度，课前复习2分钟，先学5分钟，设用x分追上小明，后教5分钟，课中小结2分钟，s后s前，t前t后+1等内容，欢迎下载使用。

走过的路程和行进速度及所花时间的关系是：路程=__________， 速度=__________, 时间=__________.
例1 小明每天早上要在7：50之前赶到距家1000米的学校上学。小明以80米/分的速度出发，5分后，小明的爸爸发现他忘了带语文书。于是，爸爸立即以180米/分的速度去追小明，并且在途中追上了他 （1）爸爸追上小明用了多长时间？ （2）追上小明时，距离学校还有多远？
分析：爸爸走的路程=小明走的路程 爸爸走的时间+5分钟=小明走的时间
画出线段图，关系就清楚了。
第一次先学后教：追及（同地不同时）
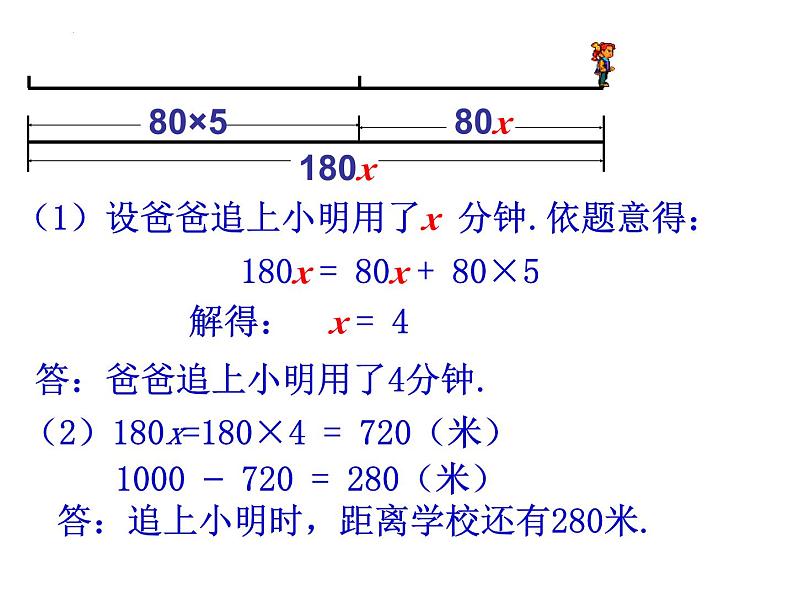
（1）设爸爸追上小明用了x 分钟.依题意得：
180x = 80x + 80×5
解得： x = 4
答：爸爸追上小明用了4分钟.
（2）180x=180×4 = 720（米）
1000 − 720 = 280（米）
答：追上小明时，距离学校还有280米.
同向而行（追及问题）条件：同地不同时，甲先走，乙后走等量关系：甲走的路程=乙走的路程；甲走的时间=乙走的时间＋时间差.
育红学校七年级学生步行到郊外旅行，七（1）班的学生组成前队，步行速度为4km/h.七（2）班的学生组成后队，速度为6km/h，前队出发1小时后，后队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑自行车速度为12km/h。根据上面的事实提出问题并尝试去解答。
（1）后队追上前队时用了多少时间？
再练：议一议（12分钟）
解：设后队用x小时追上前队，依题意得：
分析：两个等量关系： 且 ①s后=v后t后=6x②s前=v前t前=4(x+1)
6x=4(x+1)解得：x=2答：后队追上前队时用了2小时
（2）联络员总共骑了多少千米？
分析：后队走的时间=联络员骑的时间
解：12×2=24（千米）答：联络员总共骑了24千米。
例2 甲、乙两站间的路程为450km；一列慢车从甲站开出，每小时行驶65km；一列快车从乙站开出，每小时行驶85km。 （1）两车同时开出，同向而行，快车追慢车，则经过多久快车可以追上慢车？
解：设经过t小时两车相遇，依题意得：
分析：慢车走的时间=快车走的时间 慢车走的路程=快车走的路程-两地距离
65t=85t-450
答：经过22.5小时快车可以追上慢车。
第二次先学后教：追及（同时不同地）
同向而行（追及问题）条件：同时不同地，甲快，乙慢，甲追乙等量关系：甲走的时间=乙走的时间；甲走的路程=乙走的路程＋两地距离.
同向而行（追及问题）①同地不同时，甲先走，乙后走快走的路程=慢走的路程；快走的时间=慢走的时间-时间差.②同时不同地快走的时间=慢走的时间；快走的路程=慢走的路程＋两地距离.
例2 甲、乙两站间的路程为450km；一列慢车从甲站开出，每小时行驶65km；一列快车从乙站开出，每小时行驶85km。 （2）两车同时开出，相向而行，多少小时相遇？ （3）快车先开0.5小时，两车相向而行，慢车行驶多少小时两车相遇？
第三次先学后教：相遇问题（10分钟）
解：设经过x小时两车相遇，依题意得：
例2 甲、乙两站间的路程为450km；一列慢车从甲站开出，每小时行驶65km；一列快车从乙站开出，每小时行驶85km。 （2）两车同时开出，相向而行，多少小时相遇？
解： （2）设两车行驶了x小时后相遇，依题意得：
65x+85x=450
答：两车行驶了3小时后相遇。
（3）解:设慢车行驶了y小时后两车相遇，依题意得：
65y+85y+85x0.5=450
答：慢车行驶了2小时43分后两车相遇。
例2 甲、乙两站间的路程为450km；一列慢车从甲站开出，每小时行驶65km；一列快车从乙站开出，每小时行驶85km。 （3）快车先开0.5小时，两车相向而行，慢车行驶多少小时两车相遇？
相向行驶（相遇问题）条件：甲乙两方经过一段时间相遇等量关系：甲走的路程+乙走的路程=两地距离
例3 一船行于A、B两码头之间，顺水航行需3小时，逆水航行需5小时，已知水流速度是4km/h,求这两码头之间的距离。
解：设两码头之间的距离为xkm,则船顺水航行的速度为 km/h,逆水航行的速度为 km/h,依题意得：
答：这两个码头之间的距离为60km.
分析： 顺水速度=静水速度+水速 逆水速度=静水速度-水速 静水速度=顺水速度-水速=逆水速度+水速
第四次先学后教：航行问题（10分钟）
例4 一架飞机飞行两城之间，顺风时需要5小时， 逆风时需要6小时，已知两地距离为30千米，求风速。
解：设风速为x公里/小时，依题意得：
答：风速为0.5千米/小时。
分析：飞行问题也是行程问题。同水流问题一样，飞行问题的等量关系有：顺风飞行速度=飞机本身速度+风速，逆风飞行速度=飞机本身速度-风速。
船，飞机的行程问题（航行问题）条件：顺流逆流往返两地等量关系：（飞行同下）顺水速度=静水速度+水速 逆水速度=静水速度-水速 静水速度=顺水速度-水速=逆水速度+水速=>顺水速度-逆水速度=2×水速
例5 甲和乙在400米长的环形跑道上练习赛跑，甲的速度是8米/秒，乙的速度是7米/秒。若两人同时同地同向而行，问经过多少秒后甲追上乙？
分析：本题是追及问题，当甲追乙时，表示甲超出乙一圈，即用相同的时间，甲多跑了400米。
解：设经过x秒后甲追上乙，依题意得：
答：经过400秒后甲追上乙.
第五次先学后教：环形追及问题
环形追及问题条件：两人同时同地同方向追及等量关系：快人跑的时间=慢人跑的时间快人跑的路程=慢人跑的路程+一圈距离
例4 甲和乙在400米长的环形跑道上练习赛跑，甲的速度是8米/秒，乙的速度是7米/秒。若两人同时同地反向而行，问经过多少秒后两人首次相遇？
分析：相遇时，两人路程和是环形跑道的一圈，因此，甲跑的路程+乙跑的路程=400米。
解：设经过x秒后两人首次相遇，依题意得：
所以经过 秒后两人首次相遇。
第六次先学后教：环形相遇问题
环形相遇问题条件：两人同时同地反方向相遇等量关系：快人跑的时间=慢人跑的时间快人跑的路程+慢人跑的路程=一圈距离
1、敌我两方相距25千米，敌军以每小时5千米速度逃跑，我军同时以每小时8千米的速度追击，并在相距1千米处发生战斗，问战斗是在开始追后几小时发生的？
分析：此题是追及问题，等量关系式为我军追及的距离+1km=敌人逃跑的距离+25km.
解：设战斗是在开始追及后x小时发生，依题意得：
8x-5x=25-1 解得： x=8
答：8小时后战斗开始。
2、甲、乙两人在环形跑道上练习跑步，已知环形跑道一圈400米，乙每秒钟跑6米，甲的速度是乙的 倍。如果甲在乙前面8米处同时同地同向出发，那么经过多少秒甲追上乙？
解：设经过x秒甲追上乙，依题意得：
6× x=6x+400-8 x=196
所以经过196秒甲、乙两人首次相遇。
1、A、B两地相距448千米，一列慢车从A地出发每小时行驶60千米，一列快车从B地行驶出发每小时行驶80千米，两车相向而行，慢车先行28分钟，快车开出后多长时间相遇？
解：设快车行x小时后相遇，依题意得：
60x( +x)+80x=448 x=3
所以快车开出3小时后相遇。
2、甲、乙两人在环形跑道上练习跑步，已知环形跑道一圈400米，乙每秒钟跑6米，甲的速度是乙的 倍。如果甲乙两人相距8米，同时反向出发，那么经过多少秒两人首次相遇？
解：设经过x秒甲、乙两人首次相遇，依题意得：
6× x+6x=400-8 x=28
所以经过28秒甲、乙两人首次相遇.