





北师大版七年级上册5.6 应用一元一次方程——追赶小明优秀ppt课件
展开1.学会利用线段图分析行程问题,寻找等量关系,建立数学模型.(难点)2.能利用行程中的速度、路程、时间之间的关系列方程解应用题.(重点)
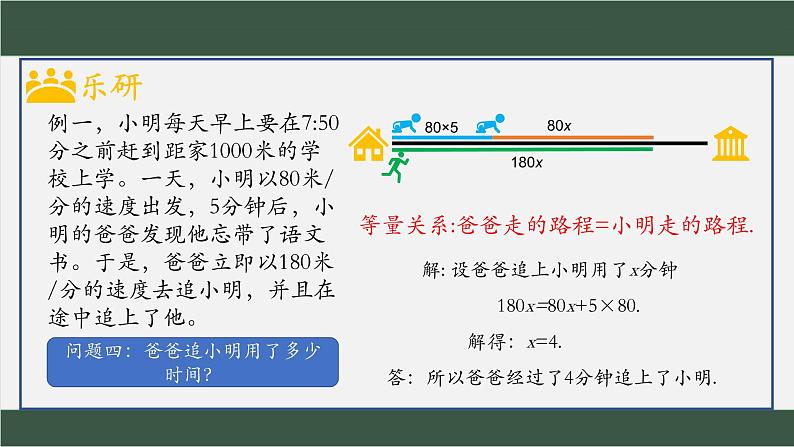
例一,小明每天早上要在7:50分之前赶到距家1000米的学校上学。一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘带了语文书。于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他。
问题一:在整个过程中,小明走的路程分为几个部分
答:整个过程分成两个部分,分别为追赶前走的路程和追赶时走的路程
问题二:在整个过程中,小明爸爸走的路程分为几个部分
答:整个过程中小明爸爸走的路程为追赶时走的路程
问题三:在整个过程中,小明走的路程和爸爸走的路程是什么关系?
答:小明走的路程和小明爸爸走的路程相同
你能通过一定的示意图把整个过程表示出来吗?
等量关系:爸爸走的路程=小明走的路程.
解: 设爸爸追上小明用了x分钟
180x=80x+5×80.
答:所以爸爸经过了4分钟追上了小明.
问题四:爸爸追小明用了多少时间?
等量关系:家离学校的距离-爸爸走的路程=距离学校的距离.
解: 由问题四可知,爸爸用了4分钟追上小明
答:爸爸追上小明时距学校还有280米.
问题五:追上小明时,距离学校多远
1000-180×4= 280(米).
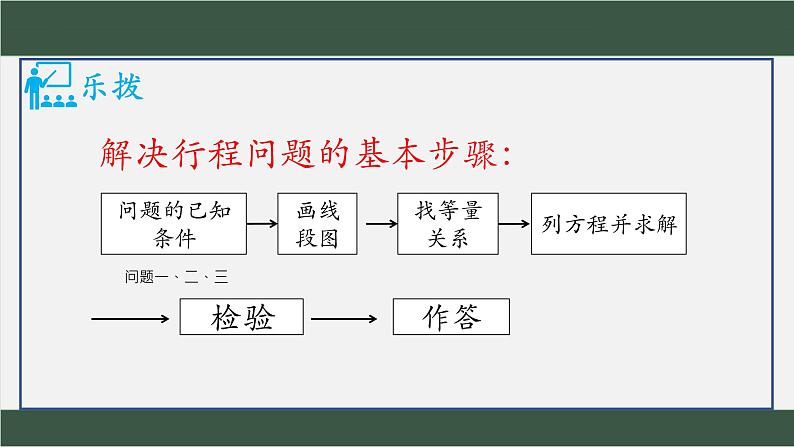
解决行程问题的基本步骤:
1. 例1的题目属于行程问题的哪一类型?
A.相遇问题 B.追及问题
2.追及问题有这几种情况,该题属于哪种类型?
例2 小彬和小强每天早晨坚持跑步,小彬每秒跑 4米,小强每秒跑6米.如果小强站在百米跑道起跑处,小彬站在他前面10米处,两人同时同向起跑,几秒后小强能追上小彬?
问题一:小彬和小强是同时出发吗?
问题二:既然是同时出发,为什么会出现一个人追另一个人的现象呢?
答:小彬和小强是同时同向出发
答:小彬站在小强前面10米处
追及问题有这几种情况,该题属于哪种类型?
小彬每秒跑 4米,小强每秒跑6米. 小彬站在他前面10米处,两人同时同向起跑,
等量关系:小彬跑的路程+10m=小强跑的路程.
解:设经过 x 秒后小强追上小彬。 4x+10 = 6x 解得:x = 5.答:经过5秒后小强追上小彬.
(2)同时不同地慢者所行路程 + 两者距离 = 快者所行的路程
(1)同地不同时:慢者先行的路程 + 慢者被追及的路程 = 快者追及的路程
180x= 80x +5×80
180x-80x=5×80
(180-80)x=5×80
(6-4) x= 10
速度差×追击时间=需要追击的路程
例3 小彬和小强每天早晨坚持跑步,小彬每秒跑 4米,小强每秒跑6米.如果小强站在百米跑道起跑处,小彬站在他前面10米处,小彬先跑3秒,小刚再出发同向起跑,几秒后小强能追上小彬?
小彬每秒跑 4米,小强每秒跑6米. 小彬站在他前面10米处,小彬先跑3秒两人同时同向起跑,
等量关系:小彬和小强同时跑的路程+小彬先跑的路程+10m=小强跑的路程.
解:设经过x秒后小强追上小彬,4x+10+3×4=6x 解得:x=11.答:经过11秒后小强追上小彬.
关系式:速度差×追击时间=需要追击的路程
解:设经过x秒后小强追上小彬,(6-4)x=10+3×4 解得:x=11.答:经过11秒后小强追上小彬.
通过刚才的推导,例一、例二和例三都能通过“速度差×追击时间=需要追击的路程”得到,那“需要追击的路程” 在不同的追击问题中该如何寻找呢?
例1 小明每天早上要在7:50分之前赶到距家1000米的学校上学。一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘带了语文书。于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他。
例一是哪种类型的追击问题?
例一是同地不同时的追及问题
观察图像可知“需要追击的路程”为小明先走的路程。
同地不同时的追击问题:“需要追击的路程” =先走的路程
例二是哪种类型的追击问题?
例二是同时不同地的追及问题
观察图像可知“需要追击的路程”为两人同时运动时两人的距离。
同时不同地的追击问题:“需要追击的路程” =两人同时运动时两人的距离
例3 小彬和小强每天早晨坚持跑步,小彬每秒跑 4米,小强每秒跑6米.如果小强站在百米跑道起跑处,小彬站在他前面10米处,小彬先跑3秒,小刚再出发同向起跑,几秒后小强能追上小彬?
观察图像可知“需要追击的路程”为小彬先走的路程+两人同时运动时两人间的距离。
例三是哪种类型的追击问题?
例三是不同时不同地的追及问题
不同地不同时的追击问题:“需要追击的路程” =先走的路程+两人同时运动时两人间的距离
若小明到校后发现忘带语文书,打电话通知爸爸来.爸爸立即以180米/分的速度从家里出发,同时小明以120米/分的速度从学校返回,两人几分钟相遇?
等量关系:小明的路程+爸爸的路程=家到学校的总路程
若小明到校后,小明的爸爸发现他忘带语文书,于是立即以180米/分的速度去送书,2分钟后,小明发现自己未带书,于是立即以140米/分的速度往家返,小明和爸爸在途中相遇.(1)问小明走了多长时间和爸爸相遇?
等量关系:小明返回的路程+爸爸的路程=家到学校的总路程
两者所走的路程之和 = 总路程
(3)不同时不同地慢者同时跑的路程+慢者先跑的路程+两人的起始距离=快者跑的路程.
数学5.6 应用一元一次方程——追赶小明课文配套课件ppt: 这是一份数学5.6 应用一元一次方程——追赶小明课文配套课件ppt,共27页。PPT课件主要包含了速度×时间,路程÷时间,路程÷速度,课前复习2分钟,先学5分钟,设用x分追上小明,后教5分钟,课中小结2分钟,s后s前,t前t后+1等内容,欢迎下载使用。
北师大版七年级上册5.6 应用一元一次方程——追赶小明一等奖课件ppt: 这是一份北师大版七年级上册5.6 应用一元一次方程——追赶小明一等奖课件ppt,共25页。PPT课件主要包含了学习目标,情境导入,探究新知,追及问题,归纳总结,甲的行程+乙的行程,甲的行程,乙的行程,注意单位统一,做一做等内容,欢迎下载使用。
2021学年5.6 应用一元一次方程——追赶小明教学ppt课件: 这是一份2021学年5.6 应用一元一次方程——追赶小明教学ppt课件,共26页。PPT课件主要包含了龟兔赛跑,行程问题,请用线段图表示,小明所跑的路程,小彬所跑的路程,小强所跑的路程,追及问题同向同时,甲在前乙在后,相遇问题相向而行,归纳小结等内容,欢迎下载使用。












