2024年中考数学一轮复习《正方形》考点课时精炼(含答案)

这是一份2024年中考数学一轮复习《正方形》考点课时精炼(含答案)，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
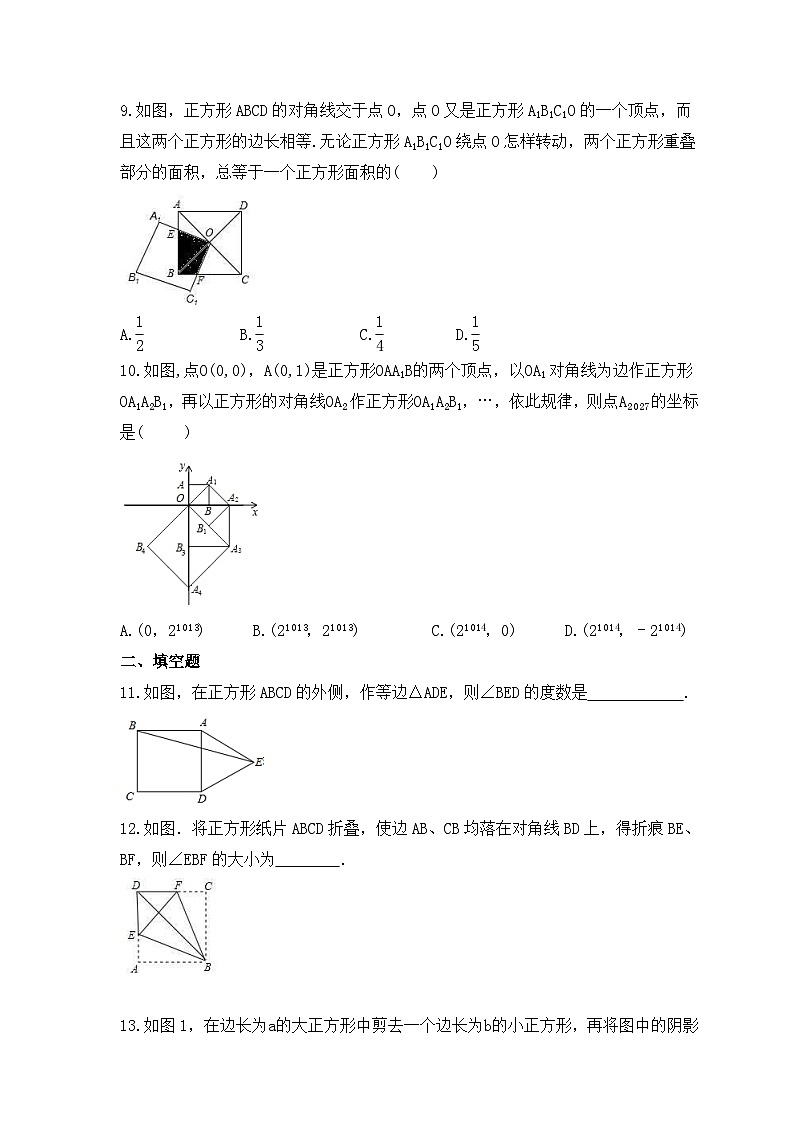
2024年中考数学一轮复习《正方形》考点课时精炼一              、选择题1.如图，平行四边形、矩形、菱形、正方形的包含关系可用如图表示，则图中阴影部分所表示的图形是(　　)A.矩形        B.菱形        C.矩形或菱形        D.正方形2.如图，四边形ABCD是正方形，延长AB到点E，使AE＝AC，则∠BCE的度数是(　　)A.22.5°         B.25°          C.23°           D.20°3.如图，已知菱形ABCD，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为(　　)A.16          B.12          C.24           D.184.如图，E是正方形ABCD的边BC延长线上一点，且CE＝AC，则∠E＝(　　)A.90°      B.45°     C.30°    D.22.5°5.将一正方形纸片按图中⑴、⑵的方式依次对折后，再沿⑶中的虚线裁剪，最后将⑷中的纸片打开铺平，所得图案应该是下面图案中的(   )6.如图所示，两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动，下列说法错误的是(　　)A.四边形ACDF是平行四边形B.当点E为BC中点时，四边形ACDF是矩形C.当点B与点E重合时，四边形ACDF是菱形D.四边形ACDF不可能是正方形7.下列叙述，错误的是(　　)A.对角线互相垂直且相等的平行四边形是正方形 B.对角线互相垂直平分的四边形是菱形 C.对角线互相平分的四边形是平行四边形 D.对角线相等的四边形是矩形8.已知一个无盖长方体的底面是边长为1的正方形，侧面是长为2的长方形，现展开铺平.如图，依次连结点A，B，C，D得到一个正方形，将周围的四个长方形沿虚线剪去一个直角三角形，则所剪得的直角三角形较短直角边与较长直角边的比是(　　)A.                            B.                        C.                            D.9.如图，正方形ABCD的对角线交于点O，点O又是正方形A1B1C1O的一个顶点，而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动，两个正方形重叠部分的面积，总等于一个正方形面积的(　　)A.                          B.                          C.         D.10.如图,点O(0,0)，A(0,1)是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA1A2B1，…，依此规律，则点A2027的坐标是(     )A.(0，21013)      B.(21013，21013)         C.(21014，0)      D.(21014，﹣21014)二              、填空题11.如图，在正方形ABCD的外侧，作等边△ADE，则∠BED的度数是　　　　　　.12.如图．将正方形纸片ABCD折叠，使边AB、CB均落在对角线BD上，得折痕BE、BF，则∠EBF的大小为　　　　． 13.如图1，在边长为a的大正方形中剪去一个边长为b的小正方形，再将图中的阴影部分剪拼成一个长方形，如图2．这个拼成的长方形的长为30，宽为20．则图2中Ⅱ部分的面积是        ．14.若正方形的面积是9，则它的对角线长是     .15.如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE＝30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q.若PQ＝AE，则AP等于_______cm.16.如图，线段AC＝n＋1(其中n为正整数)，点B在线段AC上，在线段AC同侧作正方形ABMN及正方形BCEF，连接AM、ME、EA得到△AME.当AB＝1时，△AME的面积记为S1；当AB＝2时，△AME的面积记为S2；当AB＝3时，△AME的面积记为S3；则S3﹣S2＝　   　.三              、解答题17.如图，已知点E，F，P，Q分别是正方形ABCD的四条边上的点，并且AF＝BP＝CQ＝DE．求证：(1)EF＝FP＝PQ＝QE；(2)四边形EFPQ是正方形．18.如图，菱形ABCD的对角线AC、BD相交于点O，分别延长OA、OC到点E、F，使AE＝CF，依次连接B、F、D、E各点.(1)求证：△BAE≌△BCF；(2)若∠ABC＝50°，则当∠EBA＝________°时，四边形BFDE是正方形.    19.如图，已知在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．(1)求证：AP＝BQ；(2)在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．          20.如图，在正方形ABCD中，E，F分别为AD，CD边上的点，BE，AF交于点O，且AE＝DF．(1)求证：△ABE≌△DAF；(2)若BO＝4，DE＝2，求正方形ABCD的面积．     21.如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G．(1)证明：△ADG≌△DCE；(2)连接BF，证明：AB＝FB．          22.如图，在正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B，直角顶点P在射线AC上移动，另一边交DC于点Q.(1)如图①，当点Q在DC边上时，猜想并写出PB与PQ所满足的数量关系，并加以证明；(2)如图②，当点Q落在DC的延长线上时，猜想并写出PB与PQ满足的数量关系，并证明你的猜想.                    23.在几何探究问题中，经常需要通过作辅助线(如，连接两点，过某点作垂线，作延长线，作平行线等等)把分散的条件相对集中，以达到解决问题的目的.(1)(探究发现)如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF＝45°，连接EF.通过探究，可发现BE，EF，DF之间的数量关系为________(直接写出结果).(2)(验证猜想)同学们讨论得出下列三种证明思路(如图1)：思路一：过点A作AG⊥AE，交CD的延长线于点G.思路二：过点A作AG⊥AE，并截取AG＝AE，连接DG.思路三：延长CD至点G，使DG＝BE，连接AG.请选择一种思路证明(探究发现)中的结论.(3)(应用)如图2，点E，F分别在正方形ABCD的边BC，CD上，且BC＝3BE， ∠EAF＝45°，设BE＝t，试用含t的代数式表示DF的长.
参考答案1.D.2.A3.A.4.D5.B.6.B.7.D.8.C.9.C.10.B11.答案为：45°.12.答案为：45°．13.答案为：100.14.答案为：3.15.答案为：1或2.16.答案为：.17.证明：(1)∵四边形ABCD是正方形，∴∠A＝∠B＝∠C＝∠D＝90°，AB＝BC＝CD＝AD，∵AF＝BP＝CQ＝DE，∴DF＝CE＝BQ＝AP，在△APF和△DFE和△CEQ和△BQP中，，∴△APF≌△DFE≌△CEQ≌△BQP(SAS)，∴EF＝FP＝PQ＝QE；(2)∵EF＝FP＝PQ＝QE，∴四边形EFPQ是菱形，∵△APF≌△BQP，∴∠AFP＝∠BPQ，∵∠AFP＋∠APF＝90°，∴∠APF＋∠BPQ＝90°，∴∠FPQ＝90°，∴四边形EFPQ是正方形．18.证明：(1)在菱形ABCD中，BA＝BC，∴∠BAC＝∠BCA，∴∠BAE＝∠BCF.在△BAE与△BCF中，BA＝BC，∠BAE＝∠BCF，AE＝CF∴△BAE≌△BCF(SAS).(2)20.19.证明：(1)∵正方形ABCD∴AD＝BA，∠BAD＝90°，即∠BAQ＋∠DAP＝90°∵DP⊥AQ∴∠ADP＋∠DAP＝90°∴∠BAQ＝∠ADP∵AQ⊥BE于点Q，DP⊥AQ于点P∴∠AQB＝∠DPA＝90°∴△AQB≌△DPA(AAS)∴AP＝BQ(2)①AQ﹣AP＝PQ②AQ﹣BQ＝PQ③DP﹣AP＝PQ④DP﹣BQ＝PQ20.证明：(1)∵四边形ABCD是正方形，∴AB＝AD，∠BAE＝∠D＝90°，又AE＝DF，∴△ABE≌△DAF；(2)∵△ABE≌△DAF，∴∠FAD＝∠ABE，又∠FAD＋∠BAO＝90°，∴∠ABO＋∠BAO＝90°，∴△ABO∽△EAB，∴AB：BE＝BO：AB，即AB：6＝4：AB，∴AB2＝24，所以正方形ABCD面积是24．21.解：(1)∵四边形ABCD是正方形，∴∠ADG＝∠C＝90°，AD＝DC，又∵AG⊥DE，∴∠DAG＋∠ADF＝90°＝∠CDE＋∠ADF，∴∠DAG＝∠CDE，∴△ADG≌△DCE(ASA)；(2)如图所示，延长DE交AB的延长线于H，∵E是BC的中点，∴BE＝CE，又∵∠C＝∠HBE＝90°，∠DEC＝∠HEB，∴△DCE≌△HBE(ASA)，∴BH＝DC＝AB，即B是AH的中点，又∵∠AFH＝90°，∴Rt△AFH中，BF＝AH＝AB．22.解：(1)PB＝PQ.证明：连接PD，∵四边形ABCD是正方形，∴∠ACB＝∠ACD，∠BCD＝90°，BC＝CD，又∵PC＝PC，∴△DCP≌△BCP(SAS)，∴PD＝PB，∠PBC＝∠PDC，∵∠PBC＋∠PQC＝180°，∠PQD＋∠PQC＝180°，∴∠PBC＝∠PQD，∴∠PDC＝∠PQD，∴PQ＝PD，∴PB＝PQ(2)PB＝PQ.证明：连接PD，同(1)可证△DCP≌△BCP，∴PD＝PB，∠PBC＝∠PDC，∵∠PBC＝∠Q，∴∠PDC＝∠Q，∴PD＝PQ，∴PB＝PQ.23.解：(1)EF＝BE＋DF.(2)思路三：延长CD至点G，使DG＝BE，连接AG.∵正方形ABCD∴AB＝AD，∠B＝∠ADC＝90°∵BE＝DG∴△ABE≌△ADG(SAS)∴AE＝AG,∠BAE＝∠DAG∵∠EAF＝45°，∴∠BAE＋∠DAF＝45°∴∠GAF＝∠GAD＋∠DAF＝45°∴∠GAF＝∠EAF∴AF＝AF∴△EAF≌△GAF(SAS)∴EF＝GF＝BE＋DF.(3)由题意可知，CE＝2t，设DF＝x，则CF＝3t-x，EF＝2t＋x,∴在RtCEF中，EF2＝CE2＋CF2，∴(x＋t)2＝(3t-x)2＋(2t)2∴x＝t.即DF＝t.