

2021北京石景山高一(上)期末数学(教师版)
展开2021北京石景山高一(上)期末
数 学
一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1. 已知集合A={1,2,3,4},B={2,4,6,8},则AB中元素个数为
A. 1 B. 2 C. 3 D. 4
2. 当时,在同一坐标系中,函数与的图象是( ).
A. B. C. D.
3. 已知,则“”是“”( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分又非必要条件
4. 下列函数中,在区间上为减函数的是( )
A. B. C. D.
5. 若则一定有
A. B. C. D.
6. 已知函数为奇函数,且当x > 0时,=x2+,则等于( )
A. -2 B. 0
C. 1 D. 2
7. 已知函数,在下列区间中,包含零点的区间是
A. B. C. D.
8. 设,,,则( )
A. B. C. D.
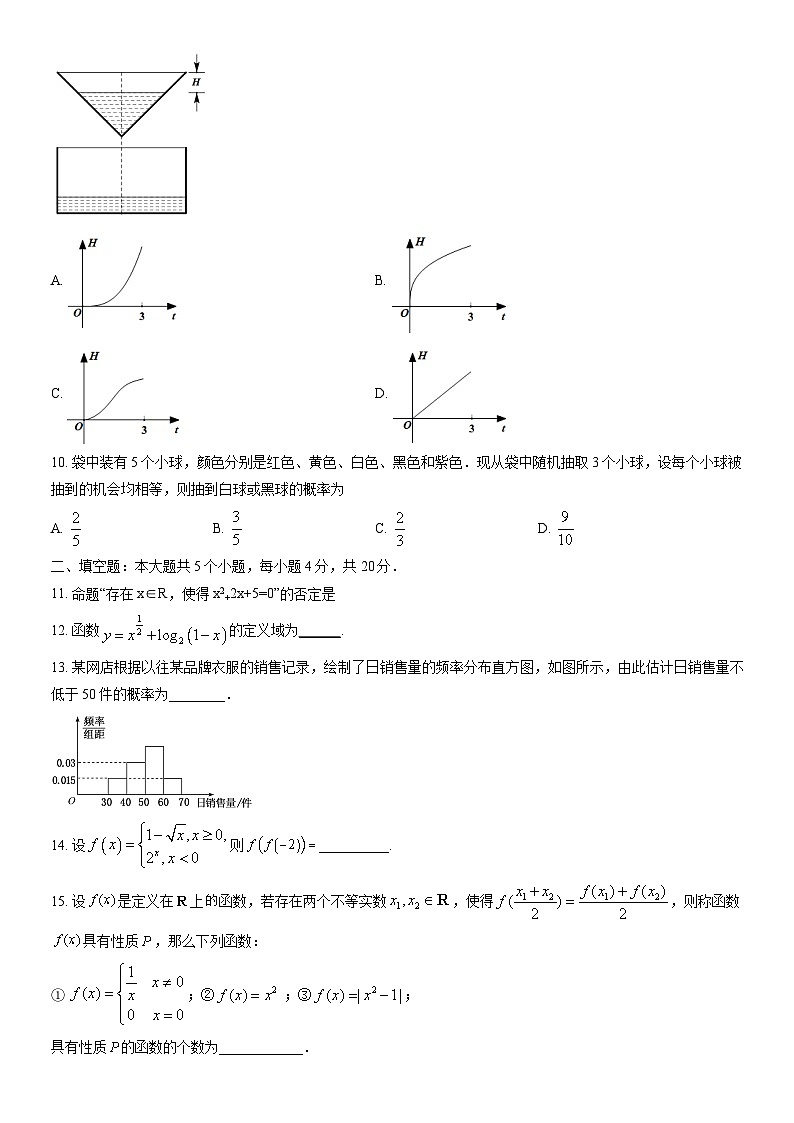
9. 如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间(分)的函数关系表示的图象只可能是( )
A. B.
C. D.
10. 袋中装有5个小球,颜色分别是红色、黄色、白色、黑色和紫色.现从袋中随机抽取3个小球,设每个小球被抽到的机会均相等,则抽到白球或黑球的概率为
A. B. C. D.
二、填空题:本大题共5个小题,每小题4分,共20分.
11. 命题“存在x∈R,使得x2+2x+5=0”的否定是
12. 函数的定义域为______.
13. 某网店根据以往某品牌衣服的销售记录,绘制了日销售量的频率分布直方图,如图所示,由此估计日销售量不低于50件的概率为________.
14. 设则__________.
15. 设是定义在上函数,若存在两个不等实数,使得,则称函数具有性质,那么下列函数:
① ;② ;③;
具有性质的函数的个数为____________.
三、解答题:本大题共5个小题,共40分.应写出文字说明,证明过程或演算步骤.
16. 已知集合,或,.
(Ⅰ)求;
(Ⅱ)求.
17. 某篮球队在本赛季已结束的8场比赛中,队员甲得分统计的茎叶图如下:
(1)求甲在比赛中得分的均值和方差;
(2)从甲比赛得分在分以下的场比赛中随机抽取场进行失误分析,求抽到场都不超过均值的概率.
18. 对于四个正数,如果,那么称是的“下位序对”.
(1)对于,试求的“下位序对”;
(2)设均为正数,且是的“下位序对”,试判断之间的大小关系.
19. 已知函数.
(1)求函数的定义域及的值;
(2)判断函数奇偶性;
(3)判断在上的单调性,并给予证明.
20. 某工厂某种航空产品年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
参考答案
一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1. 已知集合A={1,2,3,4},B={2,4,6,8},则AB中元素的个数为
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
【详解】由题意可得,故中元素的个数为2,所以选B.
【名师点睛】集合基本运算的关注点:
(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.
(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图.
2. 当时,在同一坐标系中,函数与的图象是( ).
A. B. C. D.
【答案】B
【解析】
【分析】
根据时指数函数与对数函数均为定义域内的增函数即可得答案.
【详解】解:因,函数为指数函数,为对数函数,
故指数函数与对数函数均为定义域内的增函数,
故选:B.
3. 已知,则“”是“”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分又非必要条件
【答案】A
【解析】
【分析】“a>1”⇒“”,“”⇒“a>1或a<0”,由此能求出结果.
【详解】a∈R,则“a>1”⇒“”,
“”⇒“a>1或a<0”,
∴“a>1”是“”的充分非必要条件.
故选A.
【点睛】充分、必要条件的三种判断方法.
1.定义法:直接判断“若则”、“若则”的真假.并注意和图示相结合,例如“⇒”为真,则是的充分条件.
2.等价法:利用⇒与非⇒非,⇒与非⇒非,⇔与非⇔非的等价关系,对于条件或结论是否定式的命题,一般运用等价法.
3.集合法:若⊆,则是的充分条件或是的必要条件;若=,则是的充要条件.
4. 下列函数中,在区间上为减函数的是( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据基本初等函数的单调性及复合函数单调性求解.
【详解】当时,在上单调递减,所以在区间上为增函数;
由指数函数单调性知在区间上单调递增;
由在区间上为增函数, 为增函数,可知在区间上为增函数;
知在区间上为减函数.
故选:D
5. 若则一定有
A. B. C. D.
【答案】D
【解析】
【详解】本题主要考查不等关系.已知,所以,所以,故.故选
6. 已知函数为奇函数,且当x > 0时,=x2+,则等于( )
A. -2 B. 0
C. 1 D. 2
【答案】A
【解析】
【分析】首先根据解析式求值,结合奇函数有即可求得
【详解】∵x > 0时,=x2+
∴=1+1=2
又为奇函数
∴
故选:A
【点睛】本题考查了函数的奇偶性,结合解析式及函数的奇偶性,求目标函数值
7. 已知函数,在下列区间中,包含零点的区间是
A. B. C. D.
【答案】C
【解析】
【详解】因为,,所以由根的存在性定理可知:选C.
考点:本小题主要考查函数的零点知识,正确理解零点定义及根的存在性定理是解答好本类题目的关键.
8. 设,,,则( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据指数函数、对数函数的单调性,利用中间值比较法对三个数进行比较即可.
【详解】由函数的单调性,可知.
由函数的单调性,可知,
由函数的单调性可知,
所以.
故选:B
【点睛】方法点睛:指对数比较大小,常用的方法是:中间值分析法(与比较大小),单调性分析法(根据单调性直接写出范围).
9. 如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间(分)的函数关系表示的图象只可能是( )
A. B.
C. D.
【答案】A
【解析】
【分析】
利用特殊值法,圆柱液面上升速度是常量,表示圆锥漏斗中液体单位时间内落下相同的体积,当时间取分钟时,液面下降的高度与漏斗高度的比较.
【详解】由于所给的圆锥形漏斗上口大于下口,当时间取分钟时,液面下降的高度不会达到漏斗高度的,对比四个选项的图象可得结果.
故选:A
【点睛】本题主要考查了函数图象的判断,常利用特殊值和函数的性质判断,属于中档题.
10. 袋中装有5个小球,颜色分别是红色、黄色、白色、黑色和紫色.现从袋中随机抽取3个小球,设每个小球被抽到的机会均相等,则抽到白球或黑球的概率为
A. B. C. D.
【答案】D
【解析】
【详解】分析:先求对立事件的概率:黑白都没有的概率,再用1减得结果.
详解:从袋中球随机摸个,
有,黑白都没有只有种,
则抽到白或黑概率为.
选.
点睛:古典概型中基本事件数的探求方法
(1)列举法.
(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.
(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.
(4)排列组合法:适用于限制条件较多且元素数目较多的题目.
二、填空题:本大题共5个小题,每小题4分,共20分.
11. 命题“存在x∈R,使得x2+2x+5=0”的否定是
【答案】对任何x∈R,都有x2+2x+5≠0.
【解析】
【详解】因为命题“存在x∈R,使得x2+2x+5=0”是特称命题,根据特称命题的否定是全称命题,
可得命题的否定为:对任何x∈R,都有x2+2x+5≠0.
故答案为对任何x∈R,都有x2+2x+5≠0.
12. 函数的定义域为______.
【答案】
【解析】
【分析】
根据函数解析式,列出不等式组求解即可.
【详解】因为函数,
所以解得,
所以函数定义域为,
故答案为:
13. 某网店根据以往某品牌衣服的销售记录,绘制了日销售量的频率分布直方图,如图所示,由此估计日销售量不低于50件的概率为________.
【答案】0.55
【解析】
【分析】
用减去销量为的概率,求得日销售量不低于50件的概率.
【详解】用频率估计概率知日销售量不低于50件的概率为1-(0.015+0.03)×10=0.55.
故答案为:
【点睛】本小题主要考查根据频率分布直方图计算事件概率,属于基础题.
14. 设则__________.
【答案】
【解析】
【分析】先求,再求的值.
【详解】由分段函数可知,
.
故答案为:
【点睛】本题考查分段函数求值,属于基础题型.
15. 设是定义在上的函数,若存在两个不等实数,使得,则称函数具有性质,那么下列函数:
① ;② ;③;
具有性质的函数的个数为____________.
【答案】
【解析】
【分析】
根据题意,找出存在的点,如果找不出则需证明:不存在,,使得.
【详解】①因为函数是奇函数,可找关于原点对称的点,比如,存在;
②假设存在不相等,,使得,即,得,矛盾,故不存在;
③函数为偶函数,,令,,
则,存在.
故答案为:
【点睛】关键点点睛:证明存在性命题,只需找到满足条件的特殊值即可,反之需要证明不存在,一般考虑反证法,先假设存在,推出矛盾即可,属于中档题.
三、解答题:本大题共5个小题,共40分.应写出文字说明,证明过程或演算步骤.
16. 已知集合,或,.
(Ⅰ)求;
(Ⅱ)求.
【答案】(1)(2)
【解析】
分析】
(1)根据交集直接能算;
(2)根据补集、并集运算求解.
【详解】(1)因为,或,
所以
(2)由或,知,
所以.
17. 某篮球队在本赛季已结束的8场比赛中,队员甲得分统计的茎叶图如下:
(1)求甲在比赛中得分均值和方差;
(2)从甲比赛得分在分以下场比赛中随机抽取场进行失误分析,求抽到场都不超过均值的概率.
【答案】(1)15,32.25(2)
【解析】
【分析】
(1)由已知中的茎叶图,代入平均数和方差公式,可得得答案;
(2)根据古典概型计算即可求解.
【详解】(1)这8场比赛队员甲得分为:7,8,10,15,17,19,21,23
故平均数为:,
方差:
.
(2) 从甲比赛得分在分以下的场比赛中随机抽取场,共有15中种不同的取法,
其中抽到场都不超过均值的为得分共6种,
由古典概型概率公式得.
18. 对于四个正数,如果,那么称是的“下位序对”.
(1)对于,试求的“下位序对”;
(2)设均为正数,且是的“下位序对”,试判断之间的大小关系.
【答案】(1)(2)
【解析】
【分析】
(1) 根据新定义,代入计算判断即可;
(2)根据新定义得到ad < bc,再利用不等式的性质,即可判断.
【详解】(1),
的“下位序对”是.
(2)是的“下位序对”,
,
均为正数,
,即,
,
同理可得,
综上所述,
【点睛】关键点点睛:对于本题关键理解,如果,那么称是的“下位序对”这一新定义,理解此定义后,利用不等式性质求解即可.
19. 已知函数.
(1)求函数的定义域及的值;
(2)判断函数的奇偶性;
(3)判断在上的单调性,并给予证明.
【答案】(1)(2)偶函数(3)在上是减函数,证明见解析.
【解析】
【分析】
(1)根据对数函数成立的条件即可求函数f (x)的定义域及的值;
(2)根据函数奇偶性的定义即可判断函数的奇偶性;
( 3)利用函数单调性的定义进行判断和证明.
【详解】(1)因为,
所以,解得,
所以函数的定义域为.
(2)由(1)知函数的定义域关于原点对称,
且,
所以函数是偶函数.
(3)在上是减函数.
设,且,
则,
因为,
所以,所以,
即,
所以在上是减函数.
【点睛】方法点睛:利用定义法证明函数的单调性,第一步设且,第二步做差,变形,判断差的符号,第三步根据差的符号作出结论.
20. 某工厂某种航空产品的年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
【答案】(1);(2)年产量为件时,利润最大为万元.
【解析】
【详解】试题分析:(1)实际应用题首先要根据题意,建立数学模型,即建立函数关系式,这里,要用分类讨论的思想,建立分段函数表达式;(2)根据建立的函数关系解模,即运用数学知识求函数的最值,这里第一段,运用的是二次函数求最值,而第二段,则可运用基本不等式求最值,然后再作比较,确定最终的结果,最后要回到实际问题作答.
试题解析:解:(1)当时,;
当时,,
所以.
(2)当时,
此时,当时,取得最大值万元.
当时,
此时,当时,即时,取得最大值万元,
所以年产量为件时,利润最大为万元.
考点:函数、不等式的实际应用.
2022北京石景山高一(上)期末考试数学试卷(教师版): 这是一份2022北京石景山高一(上)期末考试数学试卷(教师版),共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021北京石景山高一(下)期末数学(教师版): 这是一份2021北京石景山高一(下)期末数学(教师版),共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022北京石景山高二(上)期末数学(教师版): 这是一份2022北京石景山高二(上)期末数学(教师版),共12页。












