北师大版九年级上册6 应用一元二次方程教学ppt课件

这是一份北师大版九年级上册6 应用一元二次方程教学ppt课件，共19页。PPT课件主要包含了建立一元二次方程模型，应用一元二次方程，谢谢大家等内容，欢迎下载使用。
想一想：列方程解应用题的一般步骤是什么？
审题，分清题意，明确题目要求，弄清已知数、未知数以及它们之间的关系；
设未知数，设未知数的方法有直接设未知数和间接设未知数两种；
根据题中的等量关系列方程；
“检验”，即验证是否符合题意；
回答题目中要解决的问题.
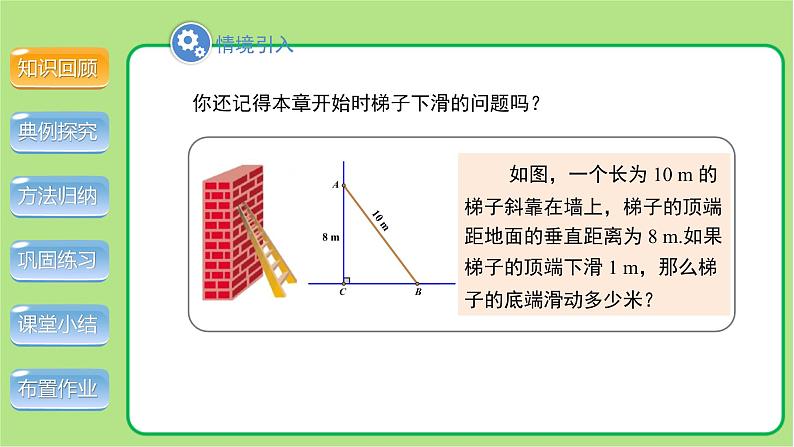
你还记得本章开始时梯子下滑的问题吗？
如图，一个长为 10 m 的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为 8 m.如果梯子的顶端下滑 1 m，那么梯子的底端滑动多少米？
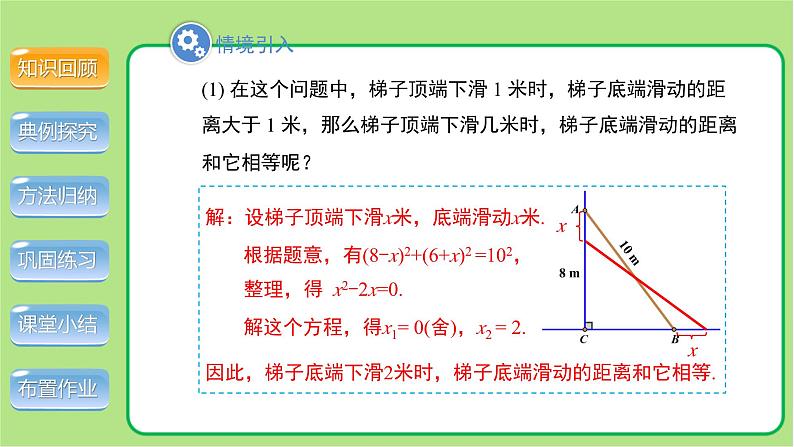
(1) 在这个问题中，梯子顶端下滑 1 米时，梯子底端滑动的距离大于 1 米，那么梯子顶端下滑几米时，梯子底端滑动的距离和它相等呢？
解：设梯子顶端下滑x米，底端滑动x米.
根据题意，有(8-x)2+(6+x)2 =102，
整理，得 x2-2x=0.
解这个方程，得x1= 0(舍)，x2 = 2.
因此，梯子底端下滑2米时，梯子底端滑动的距离和它相等.
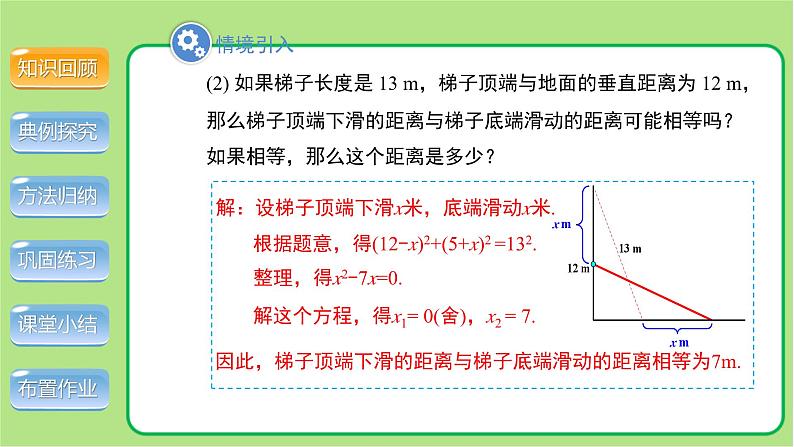
(2) 如果梯子长度是 13 m，梯子顶端与地面的垂直距离为 12 m，那么梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗？如果相等，那么这个距离是多少？
根据题意，得(12-x)2+(5+x)2 =132.
整理，得x2-7x=0.
解这个方程，得x1= 0(舍)，x2 = 7.
因此，梯子顶端下滑的距离与梯子底端滑动的距离相等为7m.
例1 如图，某海军基地位于 A 处，在其正南方向 200 n mile 处有一重要目标 B，在 B 的正东方向200 n mile 处有一重要目标C.小岛 D 位于 AC 的中点，岛上有一补给码头；小岛 F 位于 BC 中点.一艘军舰从 A 出发，经 B 到 C 匀速巡航，一艘补给船同时从 D 出发，沿南偏西方向匀速直线航行，欲将一批物品送达军舰.
已知军舰的速度是补给船的 2 倍，军舰在由 B 到 C 的途中与补给船相遇于E处，那么相遇时补给船航行了多少海里？(结果精确到0.1 n mile)
(1)要求 DE 的长，需要如何设未知数？
(4)构造出Rt△DEF 后，三条边长DE，DF，EF 分别是多少？
(2)怎样建立含 DE 未知数的等量关系？
(3)利用勾股定理建立等量关系，如何构造直角三角形？
一般求什么设什么，可设DE的长为x n mile.
连接DF，由三角形中位线得AB∥DF，从而DF⊥EF，构造出Rt△DEF.
根据已知条件，可考虑利用勾股定理建立等量关系.
DF=100 n mile，DE=x n mile，EF=AB+BF-(AB+BE)=(300-2x) n mile.
解这个方程，得 所以，相遇时补给船大约航行了 118.4 n mile.
解： 连接 DF.∵AD = CD，BF = CF，∴DF 是△ABC 的中位线.∴DF∥AB，且 DF = AB.∵AB⊥BC，AB=BC= 200 n mile，∴ DF⊥BC，DF = 100 n mile，BF = 100 n mile.设相遇时补给船航行了 x n mile，那么DE = x nmile，AB + BE = 2x n mile，EF = AB + BF -(AB + BE)=(300-2x) n mile.在Rt△DEF 中，根据勾股定理可得方程 x2 = 1002 + (300-2x)2，整理，得 3x2-1200x + 100 000 = 0.
例2 如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC向点C以2cm/s的速度移动，如果P、Q分别从A、B同时出发，那么几秒后五边形APQCD的面积为64cm2？
由S五边形APQCD =S矩形ABCD- S△PBQ，
设t秒后五边形APQCD的面积为64cm2，
则AP=tcm，BQ=2tcm，
所以PB=(6-t)cm.
可得：64 = 6×12 - 2t(6-t) ÷2.
从而求得满足条件的解即可.
解：设t秒后五边形APQCD的面积为64cm2，根据题意，得 64=6×12-2t(6-t) ÷2. 整理，得 t2 - 6t + 8 = 0.解方程，得 t1= 2，t2 =4.因此，在第2秒和第4秒时五边形的面积都是 64cm2.
这里要特别注意，在列一元二次方程解应用题时，由于所得的根一般有两个，所以要检验这两个根是否符合实际问题的要求.
运用一元二次方程模型解决实际问题的步骤有哪些？
分析数量关系 设未知数
1.《九章算术》“勾股”章有一题：“今有二人同所立，甲行率七，乙行率三，乙东行，甲南行十步而斜东北与乙会，问甲乙行各几何.”大意是说：已知甲、乙二人同时从同一地点出发，甲的速度为 7，乙的速度为 3.乙一直向东走，甲先向南走了 10 步，后又斜向北偏东方向走了一段后与乙相遇.那么相遇时，甲、乙各走了多远？
设甲乙两人走的时间为x，则甲走的路程为3x，乙走的路程为7x，依题意得：
所以，相遇时，甲走了10.5步，乙走了24.5步.
解：如图所示，甲、乙二人同时从点O出发，在点B处相遇.
2.有这样一道阿拉伯古算题：有两笔钱，一多一少，其和等于 20，积等于 96，多的一笔钱被许诺赏给赛义德，那么赛义德得到多少钱？
解: 设较多的钱为 x，则较少的为(20-x).由题意，可得 x(20- x)＝96.解得 x1＝12，x2＝8 (舍去)．所以，赛义德得到的钱数为12.
3.如图：在 Rt△ACB 中，∠C = 90°，点 P、Q 同时由A、B 两点出发分别沿 AC、BC 方向向点 C 匀速移动，它们的速度都是 1 m/s，几秒后△PCQ 的面积为Rt△ACB 面积的一半？
解: 设经过 t s，△PCQ 面积为 Rt△ACB 面积的一半． 根据题意，得 (8－t)(6－t)＝ ×6×8× ，解方程，得 t1＝2，t2＝12 (舍去)．所以，2 s后△PCQ 面积为 Rt△ACB 面积的一半．
4.如图，一条水渠的断面为梯形，已知断面的面积为 0.78 m2，上口比渠底宽 0.6 m，渠深比渠底少 0.4 m，求渠深.
解：设渠深为 x m，则渠底为 (x＋0.4) m．S ＝ [(x＋0.4＋0.6＋x＋0.4)]x ＝ 0.78.解得 x1＝–1.3(舍去)，x2＝0.6．所以，渠深 0.6 m．
(x+0.4+0.6) m
审、设、列、解、检、答
注意：在列一元二次方程解应用题时，由于所得的根一般有两个，所以要检验这两个根是否符合实际问题的要求.
教科书第55页习题2.9 第4题
敬请各位老师提出宝贵意见！