



押中考数学第25-26题(解答压轴题:几何探究)-备战2023年中考数学临考题号押题(全国通用)
展开押中考数学第25-26题(解答压轴题:几何探究)
专题诠释:几何探究题型是中考数学常见的题型,常以压轴题的形式出现,是数学学习中的重点也是难点。探索的问题千变万化,但少不了对图形的分析和研究,尤其是对基本图形和基本结构的认识,大题可以小作,拆分成基础问题再进行解答!
目录
模块一 〖真题回顾〗 1
知识点一:和旋转有关的几何探究 1
知识点二:和图形性质有关的探究 8
模块二 〖押题冲关〗 14
模块一 〖真题回顾〗
知识点一:和旋转有关的几何探究
1.(2022·辽宁阜新·统考中考真题)已知,四边形ABCD是正方形,△DEF绕点D旋转(DE
(1)如图1,求证:△ADE≌△CDF;
(2)直线AE与CF相交于点G.
①如图2,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图3,连接BG,若AB=4,DE=2,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
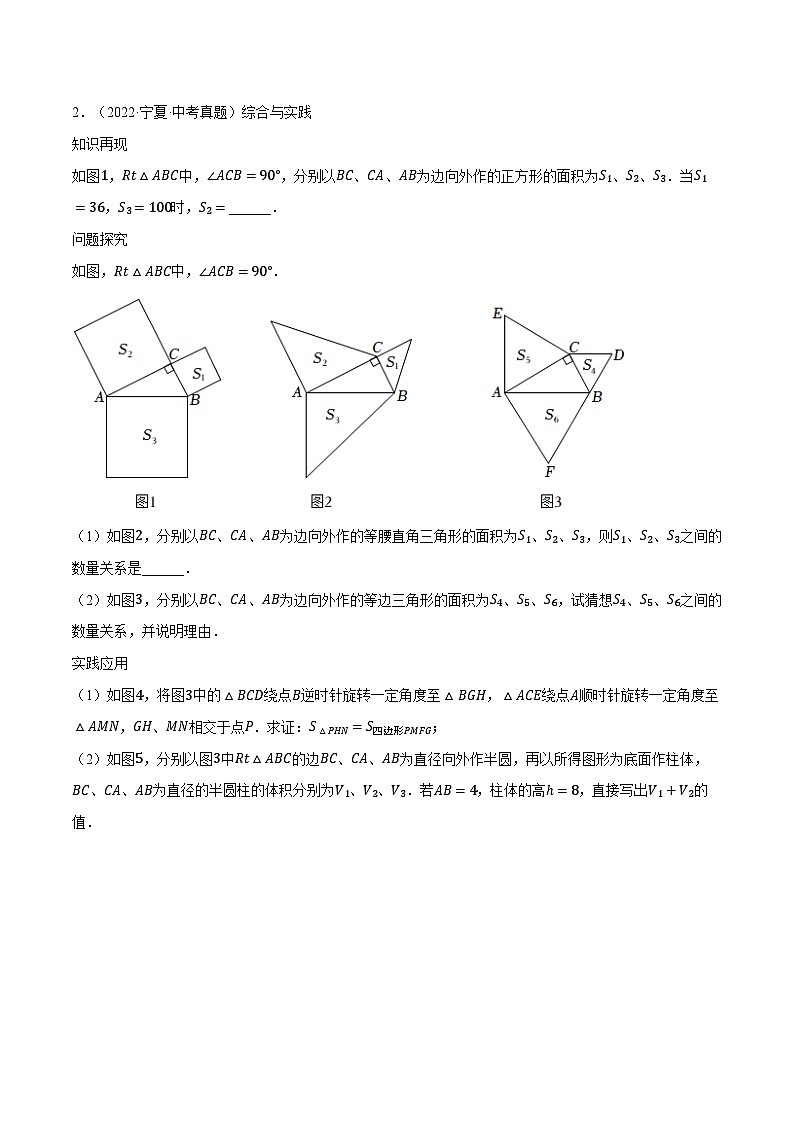
2.(2022·宁夏·中考真题)综合与实践
知识再现
如图1,Rt△ABC中,∠ACB=90°,分别以BC、CA、AB为边向外作的正方形的面积为S1、S2、S3.当S1=36,S3=100时,S2=______.
问题探究
如图,Rt△ABC中,∠ACB=90°.
(1)如图2,分别以BC、CA、AB为边向外作的等腰直角三角形的面积为S1、S2、S3,则S1、S2、S3之间的数量关系是______.
(2)如图3,分别以BC、CA、AB为边向外作的等边三角形的面积为S4、S5、S6,试猜想S4、S5、S6之间的数量关系,并说明理由.
实践应用
(1)如图4,将图3中的△BCD绕点B逆时针旋转一定角度至△BGH,△ACE绕点A顺时针旋转一定角度至△AMN,GH、MN相交于点P.求证:S△PHN=S四边形PMFG;
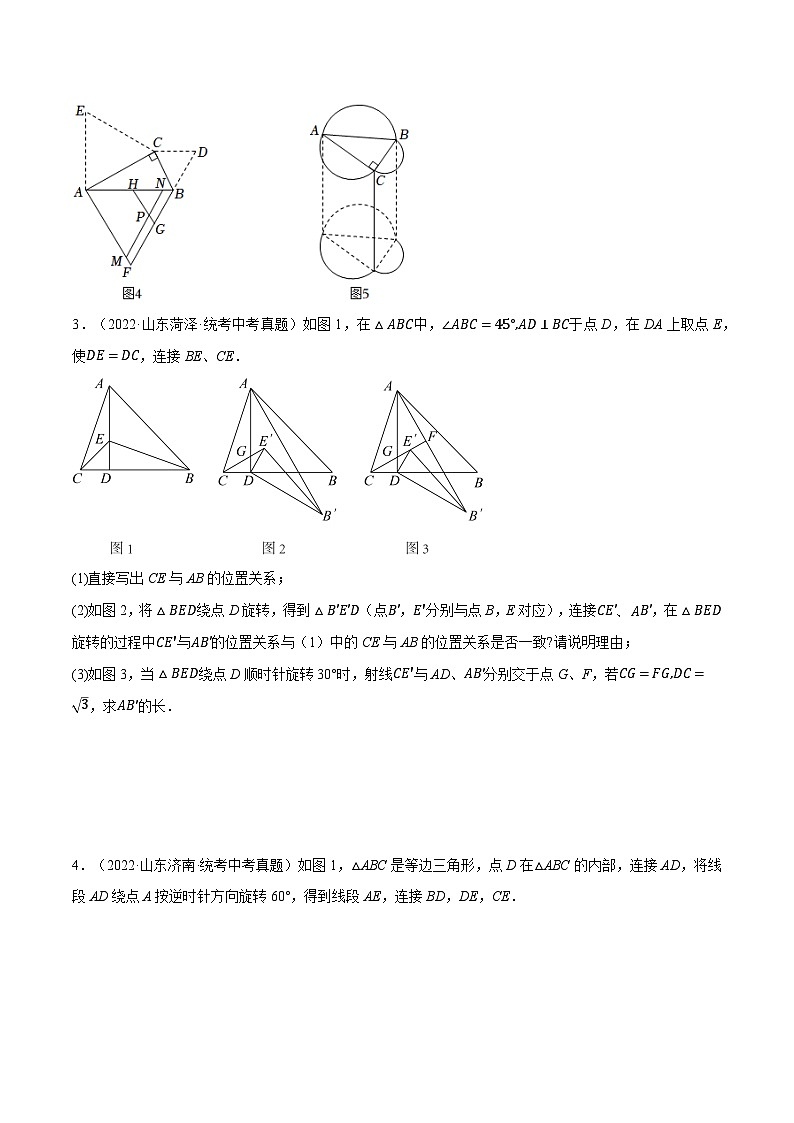
(2)如图5,分别以图3中Rt△ABC的边BC、CA、AB为直径向外作半圆,再以所得图形为底面作柱体,BC、CA、AB为直径的半圆柱的体积分别为V1、V2、V3.若AB=4,柱体的高ℎ=8,直接写出V1+V2的值.
3.(2022·山东菏泽·统考中考真题)如图1,在△ABC中,∠ABC=45°,AD⊥BC于点D,在DA上取点E,使DE=DC,连接BE、CE.
(1)直接写出CE与AB的位置关系;
(2)如图2,将△BED绕点D旋转,得到△B'E'D(点B',E'分别与点B,E对应),连接CE'、AB',在△BED旋转的过程中CE'与AB'的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;
(3)如图3,当△BED绕点D顺时针旋转30°时,射线CE'与AD、AB'分别交于点G、F,若CG=FG,DC=3,求AB'的长.
4.(2022·山东济南·统考中考真题)如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE.
(1)判断线段BD与CE的数量关系并给出证明;
(2)延长ED交直线BC于点F.
①如图2,当点F与点B重合时,直接用等式表示线段AE,BE和CE的数量关系为_______;
②如图3,当点F为线段BC中点,且ED=EC时,猜想∠BAD的度数,并说明理由.
5.(2022·江苏南通·统考中考真题)如图,矩形ABCD中,AB=4,AD=3,点E在折线BCD上运动,将AE绕点A顺时针旋转得到AF,旋转角等于∠BAC,连接CF.
(1)当点E在BC上时,作FM⊥AC,垂足为M,求证AM=AB;
(2)当AE=32时,求CF的长;
(3)连接DF,点E从点B运动到点D的过程中,试探究DF的最小值.
6.(2022·内蒙古通辽·统考中考真题)已知点E在正方形ABCD的对角线AC上,正方形AFEG与正方形ABCD有公共点A.
(1)如图1,当点G在AD上,F在AB上,求2CE2DG的值为多少;
(2)将正方形AFEG绕A点逆时针方向旋转α(0°<α<90°),如图2,求:CEDG的值为多少;
(3)AB=82,AG=22AD,将正方形AFEG绕A逆时针方向旋转α(0°<α<360°),当C,G,E三点共线时,请直接写出DG的长度.
7.(2022·山东潍坊·中考真题)【情境再现】
甲、乙两个含45°角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足O处,将甲绕点O顺时针旋转一个锐角到图②位置.小莹用作图软件Geogebra按图②作出示意图,并连接AG,BH,如图③所示,AB交HO于E,AC交OG于F,通过证明△OBE≌△OAF,可得OE=OF.
请你证明:AG=BH.
【迁移应用】
延长GA分别交HO,HB所在直线于点P,D,如图④,猜想并证明DG与BH的位置关系.
【拓展延伸】
小亮将图②中的甲、乙换成含30°角的直角三角尺如图⑤,按图⑤作出示意图,并连接HB,AG,如图⑥所示,其他条件不变,请你猜想并证明AG与BH的数量关系.
8.(2022·辽宁盘锦·中考真题)如图,四边形ABCD是正方形,△ECF为等腰直角三角形,∠ECF=90°,点E在BC上,点F在CD上,P为EF中点,连接AF,G为AF中点,连接PG,DG,将Rt△ECF绕点C顺时针旋转,旋转角为α(0°≤α≤360°).
(1)如图1,当α=0°时,DG与PG的关系为 ;
(2)如图2,当α=90°时
①求证:△AGD≌△FGM;
②(1)中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由.
9.(2022·辽宁锦州·统考中考真题)如图,在△ABC中,AB=AC=25,BC=4,D,E,F分别为AC,AB,BC的中点,连接DE,DF.
(1)如图1,求证:DF=52DE;
(2)如图2,将∠EDF绕点D顺时针旋转一定角度,得到∠PDQ,当射线DP交AB于点G,射线DQ交BC于点N时,连接FE并延长交射线DP于点M,判断FN与EM的数量关系,并说明理由;
(3)如图3,在(2)的条件下,当DP⊥AB时,求DN的长.
10.(2022·山东青岛·统考中考真题)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,将△ABC绕点A按逆时针方向旋转90°得到△ADE,连接CD.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AD方向匀速运动,速度为1cm/s.PQ交AC于点F,连接CP,EQ.设运动时间为t(s)(0
(1)当EQ⊥AD时,求t的值;
(2)设四边形PCDQ的面积为S(cm2),求S与t之间的函数关系式;
(3)是否存在某一时刻t,使PQ∥CD?若存在,求出t的值;若不存在,请说明理由.
知识点二:和图形性质有关的探究
11.(2022·吉林长春·统考中考真题)【探索发现】在一次折纸活动中,小亮同学选用了常见的A4纸,如图①,矩形ABCD为它的示意图.他查找了A4纸的相关资料,根据资料显示得出图①中AD=2AB.他先将A4纸沿过点A的直线折叠,使点B落在AD上,点B的对应点为点E,折痕为AF;再沿过点F的直线折叠,使点C落在EF上,点C的对应点为点H,折痕为FG;然后连结AG,沿AG所在的直线再次折叠,发现点D与点F重合,进而猜想△ADG≌△AFG.
【问题解决】
(1)小亮对上面△ADG≌△AFG的猜想进行了证明,下面是部分证明过程:
证明:四边形ABCD是矩形,
∴∠BAD=∠B=∠C=∠D=90°.
由折叠可知,∠BAF=12∠BAD=45°,∠BFA=∠EFA.
∴∠EFA=∠BFA=45°.
∴AF=2AB=AD.
请你补全余下的证明过程.
【结论应用】
(2)∠DAG的度数为________度,FGAF的值为_________;
(3)在图①的条件下,点P在线段AF上,且AP=12AB,点Q在线段AG上,连结FQ、PQ,如图②,设AB=a,则FQ+PQ的最小值为_________.(用含a的代数式表示)
12.(2022·贵州贵阳·统考中考真题)小红根据学习轴对称的经验,对线段之间、角之间的关系进行了拓展探究.
如图,在▱ABCD中,AN为BC边上的高,ADAN=m,点M在AD边上,且BA=BM,点E是线段AM上任意一点,连接BE,将△ABE沿BE翻折得△FBE.
(1)问题解决:
如图①,当∠BAD=60°,将△ABE沿BE翻折后,使点F与点M重合,则AMAN=______;
(2)问题探究:
如图②,当∠BAD=45°,将△ABE沿BE翻折后,使EF∥BM,求∠ABE的度数,并求出此时m的最小值;
(3)拓展延伸:
当∠BAD=30°,将△ABE沿BE翻折后,若EF⊥AD,且AE=MD,根据题意在备用图中画出图形,并求出m的值.
13.(2022·天津·统考中考真题)将一个矩形纸片OABC放置在平面直角坐标系中,点O(0,0),点A(3,0),点C(0,6),点P在边OC上(点P不与点O,C重合),折叠该纸片,使折痕所在的直线经过点P,并与x轴的正半轴相交于点Q,且∠OPQ=30°,点O的对应点O'落在第一象限.设OQ=t.
(1)如图①,当t=1时,求∠O'QA的大小和点O'的坐标;
(2)如图②,若折叠后重合部分为四边形,O'Q,O'P分别与边AB相交于点E,F,试用含有t的式子表示O'E的长,并直接写出t的取值范围;
(3)若折叠后重合部分的面积为33,则t的值可以是___________(请直接写出两个不同的值即可).
14.(2022·浙江绍兴·统考中考真题)如图,在矩形ABCD中,AB=6,BC=8,动点E从点A出发,沿边AD,DC向点C运动,A,D关于直线BE的对称点分别为M,N,连结MN.
(1)如图,当E在边AD上且DE=2时,求∠AEM的度数.
(2)当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由.
(3)当直线MN恰好经过点C时,求DE的长.
15.(2022·江苏镇江·统考中考真题)已知,点E、F、G、H分别在正方形ABCD的边AB、BC、CD、AD上.
(1)如图1,当四边形EFGH是正方形时,求证:AE+AH=AB;
(2)如图2,已知AE=AH,CF=CG,当AE、CF的大小有_________关系时,四边形EFGH是矩形;
(3)如图3,AE=DG,EG、FH相交于点O,OE:OF=4:5,已知正方形ABCD的边长为16,FH长为20,当△OEH的面积取最大值时,判断四边形EFGH是怎样的四边形?证明你的结论.
16.(2022·山东东营·统考中考真题)△ABC和△ADF均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿AB、BC运动,运动到点B、C停止.
(1)如图1,当点E、D分别与点A、B重合时,请判断:线段CD、EF的数量关系是____________,位置关系是____________;
(2)如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;
(3)当点D运动到什么位置时,四边形CEFD的面积是△ABC面积的一半,请直接写出答案;此时,四边形BDEF是哪种特殊四边形?请在备用图中画出图形并给予证明.
17.(2022·湖北襄阳·统考中考真题)矩形ABCD中,ABBC=k2(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.
(1)【特例证明】如图(1),当k=2时,求证:AE=EF;
小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
∵k=2,
∴AB=BC.
∵∠B=90°,BH=BE,
∴∠1=∠2=45°,
∴∠AHE=180°-∠1=135°.
∵CF平分∠DCG,∠DCG=90°,
∴∠3=12∠DCG=45°.
∴∠ECF=∠3+∠4=135°.
∴……
(只需在答题卡对应区域写出剩余证明过程)
(2)【类比探究】如图(2),当k≠2时,求AEEF的值(用含k的式子表示);
(3)【拓展运用】如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°,PF=5,求BC的长.
18.(2022·浙江衢州·统考中考真题)如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)求证:∠DBG=90°.
(2)若BD=6,DG=2GE.
①求菱形ABCD的面积.
②求tan∠BDE的值.
(3)若BE=AB,当∠DAB的大小发生变化时(0°<∠DAB<180°),在AE上找一点T,使GT为定值,说明理由并求出ET的值.
19.(2022·辽宁朝阳·统考中考真题)【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.
(1)小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明△ADE≌△ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.
(2)【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.
(3)【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=6,AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.
20.(2022·辽宁鞍山·统考中考真题)如图,在△ABC中,AB=AC,∠BAC=120°,点D在直线AC上,连接BD,将DE绕点D逆时针旋转120°,得到线段DE,连接BE,CE.
(1)求证:BC=3AB;
(2)当点D在线段AC上(点D不与点A,C重合)时,求CEAD的值;
(3)过点A作AN∥DE交BD于点N,若AD=2CD,请直接写出ANCE的值.
模块二 〖押题冲关〗
1.(2023·陕西西安·陕西师大附中校考模拟预测)折纸是我国传统的民间艺术,通过折纸不仅可以得到许多美丽的图形,折纸的过程还蕴含着丰富的数学知识,在综合与实践课上老师让同学们以“正方形的折叠”为主题开展了数学活动.
(1)操作判断:
在AD上选一点P,沿BP折叠,使点A落在正方形内部的点M处,把纸片展平,过M作EF∥BC交AB、CD、BP于点E、F、N,连接PM并延长交CD于点Q,连接BQ,如图①,当E为AB中点时,△PMN是________三角形.
(2)迁移探究:
如图②,若BE=5,且ME⋅MF=10,求正方形ABCD的边长.
如图③,若MNBC=1n(n>1),直接写出CQBC的值为_______.
2.(2023·安徽亳州·统考一模)综合与实践
(1)问题解决:已知四边形ABCD是正方形,以B为顶点作等腰直角三角形BEF,BE=BF,连接AE.如图1,当点E在BC上时,请判断AE和CF的关系,并说明理由.
(2)问题探究:如图2,点H是AE延长线与直线CF的交点,连接BH,将△BEF绕点B旋转,当点F在直线BC右侧时,求证:AH−CH=2BH;
(3)问题拓展:将△BEF绕点B旋转一周,当∠CFB=45°时,若AB=3,BE=1,请直接写出线段CH的长.
3.(2023·陕西西安·统考二模)问题提出
(1)如图1,⊙O是△ABC的内接圆,∠A=60°,BC=4,则⊙O半径长等于______;
问题探究
(2)如图2,在矩形ABCD中,AB=4,若在边CD上存在一点P,使得∠APB=90°,求矩形ABCD面积的最大值;
问题解决
(3)如图3,是一个矩形广场,其中AB=60m,BE足够长.为了方便居民生活,促进经济发展,街道计划在矩形内部修建一个面积尽量大的交易市场ABCD,其中C,D分别在边BE,AF上,且∠BCD=45°.在具体施工中安全联防小组要求在CD上找到一点Q,使得∠AQB=45°,以便安装摄像头对市场进行安全监管.请问满足上面要求的市场ABCD是否存在,若存在,请求出市场ABCD面积的最大值;若不存在,请说明理由.
4.(2023·江苏无锡·统考一模)如图,在矩形ABCD中,E为CD边上一点,将△BCE沿BE翻折,使点C恰好落在AD边上点F处,作∠ABF的角平分线交EF的延长线于点M,BM交AD于点N.
(1)求证:MF=NF;
(2)若AB=6,BC=10时,求MF的长;
(3)若NF=12AN+FD时,求ABBC的值.
5.(2023·广东广州·统考一模)定义新概念:有一组邻边相等,且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形ABCD,AB=BC=4,∠ABC=90°.
①若CD=3,AC⊥CD于点C,求AD的长;
②若AD=DC,∠ADC=45°,求BD的长;
(2)如图②,在矩形ABCD中AB=6,BC=15,点P是对角线BD上的一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,要使四边形ABFE是等腰直角四边形,求AE的长.
6.(2023·安徽合肥·校考一模)(1)【初步体验】如图1,正方形ABCD中,点E,F分别是AD、AB边上,且BE⊥CF于点O,求证:BE=CF.
(2)【思考探究】如图2,在(1)的条件下,连接AO并延长交BC于点G,若点G为BC边中点,求证:AE2=AF⋅AB.
(3)【灵活运用】如图3,在(2)的条件下,连接EF并延长交CB的延长线于点H,求AEGH的值.
7.(2023·山东菏泽·统考一模)实践与探究
操作一:如图①,将矩形纸片ABCD对折并展开,折痕PQ与对角线AC交于点E,连接BE,则BE与AC的数量关系为______.
操作二:如图②,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,M为AF的中点,连接DM、ME.求证:DM=ME.
拓展延伸:如图③,摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,连接AF,M为AF的中点,连接DM、ME、DE.已知正方形纸片ABCD的边长为5,正方形纸片ECGF的边长为22,求△DME的面积.
8.(2023·辽宁葫芦岛·统考一模)已知Rt△ABC中,∠C=90°,AC=BC,点E是线段AC上的动点(点E不与点A和点C重合),点F在线段BC上,线段EF绕点F逆时针旋转90°得到线段FD,点D恰好落在AB上.
(1)如图1,若EF∥AB,请直接写出线段DB和CE的数量关系;
(2)如图2,若EF与AB不平行.
①请写出线段BF,BD,CE之间的数量关系,并说明理由;
②连接DE,若AC=4,tan∠EDA=12,请直接写出线段CF的长.
9.(2023·河南洛阳·东方二中校考二模)(1)特殊发现
如图1,正方形BEFG与正方形ABCD的顶点B重合,BE,BG分别在BC、BA边上,连接DF,则有:
①DFAG=____________;②直线DF与直线AG所夹的锐角等于____________度;
(2)理解运用
将图1中的正方形BEFG绕点B逆时针旋转,连接DF、AG.
①如图2,(1)中的结论是否仍然成立?请说明理由;
②如图3,若D、F、G三点在同一直线上,且过AB边的中点O,BE=4,请求出AB的长;
(3)拓展延伸
如图4,点P是正方形ABCD的AB边上一动点(不与A、B重合),连接PC,沿PC将△PBC翻折到△PEC位置,连接DE并延长,与CP的延长线交于点F,连接AF,若AB=4PB,则DEEF的值是__________.
10.(2023·广东东莞·东莞市光明中学校考一模)【问题探究】(1)如图(1)在正方形ABCD中,AB=6,点E为DC上的点,DE=2CE,连接BE,点O为BE上的点,过点O作MN⊥BE交AD于点M,交BC于点N,则MN的长度为 .
【类比迁移】(2)如图(2)在矩形ABCD中,AB=6,BC=8,连接BD,过BD的中点O作MN⊥BD交AD于点M,交BC于点N,求MN的长度.
【拓展应用】(3)如图(3)李大爷家有一块平行四边形ABCD的菜地,测得AB=52米,BC=7米,∠ABC=45°,为了管理方便,李大爷沿着对角线BD开一条小路,过这小路的正中间,开了另一条垂直于它的小路MN(小路面积忽略不计),求新开出的小路MN的长度.
11.(2023·陕西西安·校考三模)问题提出:
(1)如图①,在△ABC中,AB=AC=13,BC=10,AD平分∠CAB交BC边于点D,点E为AC边上的一个动点,连接DE,则线段DE长的最小值为 .
问题探究:
(2)如图②,在△ABC中,∠C=90°,AC=BC=8,点D为AB边的中点,且∠EDF=90°,∠EDF的两边分别交BC、AC于点E、F.求四边形DECF的面积.
问题解决:
(3)某观光景区准备在景区内设计修建一个大型儿童游乐园.如图③,四边形ABCD为儿童游乐园的大致示意图,并将儿童游乐园分成△EDM、△BFM、△DCB和四边形AEMF四部分,其中在△EDM和△BFM两区域修建益智区,在△DCB区域修建角色游戏区,在四边形AEMF区域修建木工区.根据设计要求:四边形ABCD是平行四边形,∠ADC=60°,点E、点F、点M分别在边AD、边AB和对角线BD上,且EM=FM,∠EMF=60°,四边形AEMF的面积为2003平方米,现需在四边形ABCD的四周修建护栏起到保护乐园的作用,为了节约修建成本,四边形ABCD的周长是否存在最小值?若存在,请求出四边形ABCD周长的最小值;若不存在,请说明理由.
12.(2023·四川成都·统考二模)如图1,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D,E分别是AB,AC中点,连接DE.在同一平面内,将△ADE绕点A逆时针旋转,射线BD,CE相交于点P.
(1)如图2,在旋转过程中,∠BPC的角度是否不变?若不变,请求出∠BPC的度数.
(2)如图2,当∠BAD=120°时,求线段PC的长.
(3)连接DC,当线段PC取得最小值时,求线段DC的值.
13.(2023·江苏常州·常州实验初中校考一模)我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.
(1)概念理解:请你根据上述定义举一个等邻角四边形的例子,例如 是等邻角四边形;
(2)问题探究:如图1,在等邻角四边形ABCD中,∠DAB=∠ABC,AD,BC的垂直平分线恰好交于AB边上一点P,连接AC,BD,试探究AC与BD的数量关系,并说明理由;
(3)应用拓展:如图2,在△ABC与△ABD中,∠C=∠D=90°,BC=BD=3,AB=5,将△ABD绕着点A顺时针旋转角α0°<∠α<∠BAC得到△AB'D'(如图3),当四边形AD'BC为等邻角四边形时,求出它的面积.
14.(2023·陕西西安·高新一中校考模拟预测)问题探究:
(1)如图①,在Rt△ABC中,∠ACB=90°,AC=BC=8,以BC为直径的半圆交AB于D,P是CD上的一个动点,连接AP,则AP的最小值是____________;
(2)如图②,菱形ABCD中,AB=8,∠B=60°,点M在AD上,点N在BC上,若MN平分菱形ABCD的面积,且线段MN的长度最短,请你画出符合要求的线段MN,并求出此时MN的长度.
间题解决:
(3)合理开发利用土地资源能为人类持续创造更多财富,如图③,现有一块四边形空地ABCD计划改造利用,经测量AB=60m,AD=80m,AB∥CD,∠ABC=∠C=90°,∠D=60°,P是BC边上的一个移动观测点,过AB边上一点E修一条垂直于AP的笔直小路EF(小路宽度不计),交CD边于点F,在垂足M处建一凉亭,在凉亭M和顶点B之间修一条绿化带(宽度不计),请问是否存在EF平分四边形土地ABCD的面积?若存在,求出在EF平分四边形土地ABCD的面积时绿化带BM长度的最小值;若不存在,请说明理由.
15.(2023·江苏常州·常州市第二十四中学校考一模)如图,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.
(1)求线段CE的长.
(2)判断四边形AFGD是什么特殊四边形,并说明理由.
(3)如图,M、N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设DN=x.是否存在这样的点N,使△DMN是直角三角形?若存在,请求出x的值;若不存在,请说明理由.
16.(2023·湖北宜昌·校考一模)已知:在矩形ABCD中,ABBC=k,点P是BC上一动点(不与端点B,C重合),连接AP,PQ⊥AP于点P,交CD于点Q,连接AQ.
(1)如图1,当点P运动到BC的中点时.
①求证:△ABP∽△PCQ∽△APQ;
②若∠DAQ=60°,求k的值;
(2)如图2,当k>12时,点P在运动的过程中,是否存在点Q和点D重合的情况?若存在,试确定此时P点的位置;若不存在,请说明理由.
(3)如图3,当k=1时,PQ的延长线交正方形外角∠DCI的平分线于点G,连接AG交边CD于点H,连接PH,当AQ最小时,求PHHQ的值.
17.(2023·浙江嘉兴·统考一模)如图1,已知AB是半圆O的直径,半径OC⊥AB,D是弧BC上的动点(不含点B,C),连接AC,作BE⊥射线CD于点E.
(1)猜想∠BDE的度数,并说明理由
(2)连接OD,若OD∥AC,求证:CD=2DE.
(3)如图2,作正方形OBFC,连接OE,EF,OE交BD于点G.若OG=2GE,EF=2,求BE的长.
18.(2023·河南省直辖县级单位·校联考一模)已知△ABC和△DEB都是等腰三角形,AB=6,BD=2.
(1)当∠A=∠BDE=60°时:
①如图1,当点D在边AB上时,请直接写出CE和AD的数量关系:___________;
②如图2,当点D不在AB边上时,判断线段CE和AD的数量关系,并说明理由.
(2)如图3,当∠A=∠BDE=90°时,请直接写出CE和AD的数量关系:____________________;
(3)在(1)的条件下,将△DEB绕点B逆时针旋转α(0∘<α<360∘),当BC=CD时,请直接写出AD的长度.
19.(2023·山西晋城·统考一模)综合与实践
动手操作:
第一步:如图①,将矩形纸片ABCD沿过点O的直线折叠,使得点A,点D都落在BC边上,此时,点A与点D重合,记为E,折痕分别为BO、CO,如图②;
第二步:再沿过点O的直线折叠,使得直线OB与直线OC重合,且O、E、C三点在同一条直线上,折痕分别为OG、OH,如图③;
第三步:在图③的基础上继续折叠,使△OGB与△OHC重合,得到图④,展开铺平,连接FH,MG交于点N,如图⑤,图中的虚线为折痕.
问题解决:
(1)在图⑤中,∠BGO的度数是 ;
(2)在图⑤中,请判断四边形OFNM的形状,并说明理由;
(3)试判断线段ON与GH的数量关系,并证明;
(4)若AB=1,则AF的长是 .(提示:12+1=2−1)
20.(2023·湖南岳阳·统考一模)(1)【问题情境】如图①,在矩形ABCD中,点E、F分别在边CD、AD上,且AE⊥BF于点G,求证:BFAE=ABAD;
(2)【变式思考】如图②,在(1)的条件下,连接CG,若CG=CB,求证:点E是DC的中点;
(3)【深入探究】如图③,在矩形ABCD中,点E、F、H分别在边CD、AD、BC上,且AE⊥HF于点G,连接CG,设∠HCG=2α,且sinα=1010,若CG=CH,BHCH=m,求DEHG的值(用含m的代数式表示)
押中考数学第25-26题(解答压轴题:函数综合)-备战2023年中考数学临考题号押题(全国通用): 这是一份押中考数学第25-26题(解答压轴题:函数综合)-备战2023年中考数学临考题号押题(全国通用),文件包含押中考数学第25-26题解答压轴题函数探究解析版docx、押中考数学第25-26题解答压轴题函数探究原卷版docx等2份试卷配套教学资源,其中试卷共165页, 欢迎下载使用。
押中考数学第19-20题(解答得分题:计算或分式化简求值、几何证明、尺规作图和统计概率)-备战2023年中考数学临考题号押题(全国通用): 这是一份押中考数学第19-20题(解答得分题:计算或分式化简求值、几何证明、尺规作图和统计概率)-备战2023年中考数学临考题号押题(全国通用),文件包含押中考数学第19-20题解答得分题计算或分式化简求值几何证明尺规作图和统计概率解析版docx、押中考数学第19-20题解答得分题计算或分式化简求值几何证明尺规作图和统计概率原卷版docx等2份试卷配套教学资源,其中试卷共104页, 欢迎下载使用。
押中考数学第9-10题(选择压轴题:多结论问题)-备战2023年中考数学临考题号押题(全国通用): 这是一份押中考数学第9-10题(选择压轴题:多结论问题)-备战2023年中考数学临考题号押题(全国通用),文件包含押中考数学第9-10题多结论问题解析版docx、押中考数学第9-10题多结论问题原卷版docx等2份试卷配套教学资源,其中试卷共83页, 欢迎下载使用。












