押广东卷25题（二次函数综合）-备战 中考数学临考题号押题（广东卷）

押广东卷第25题

二次函数综合

广东中考对最后一题压轴题型二次函数知识的考查要求高，均是以10分简答题的形式进行考查，难度系数大，这几年中考命题趋势，难度可能再次提升。纵观近几年的中考试题，主要考查以下两个方面：一是考查具体二次函数的解析式．二是考查二次函数与不等式组、几何证明，存在性问题，最值问题，角度问题．

今年预测最后一题压轴题还是考查二次函数综合内容。

要求考生熟练掌握与二次函数有关的基础知识、二次函数的图象和性质以及几何相关计算与证明。能熟练求函数解析式，能根据函数图像与动点求存在性问题，角度问题，最值问题等。解答的关键是认真审题，分析图形，寻找相关联信息，利用数形结合和分类讨论的思想方法进行推理、探究和计算。

1．（2021广东）已知二次函数的图象过点，且对任意实数x，都有．

（1）求该二次函数的解析式；

（2）若（1）中二次函数图象与x轴的正半轴交点为A，与y轴交点为C；点M是（1）中二次函数图象上的动点．问在x轴上是否存在点N，使得以A、C、M、N为顶点的四边形是平行四边形．若存在，求出所有满足条件的点N的坐标；若不存在，请说明理由．

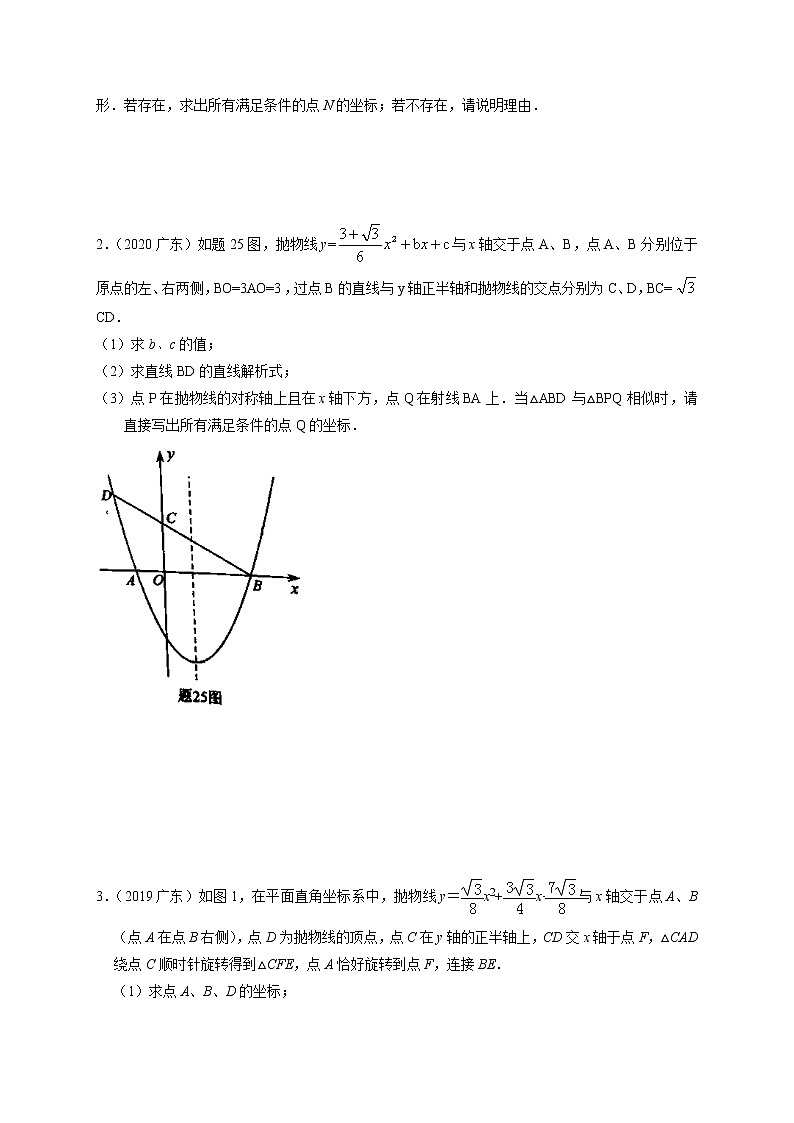
2．（2020广东）如题25图，抛物线y=与x轴交于点A、B，点A、B分别位于原点的左、右两侧，BO=3AO=3，过点B的直线与y轴正半轴和抛物线的交点分别为C、D，BC=CD．

（1）求b、c的值；

（2）求直线BD的直线解析式；

（3）点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD与△BPQ相似时，请直接写出所有满足条件的点Q的坐标．

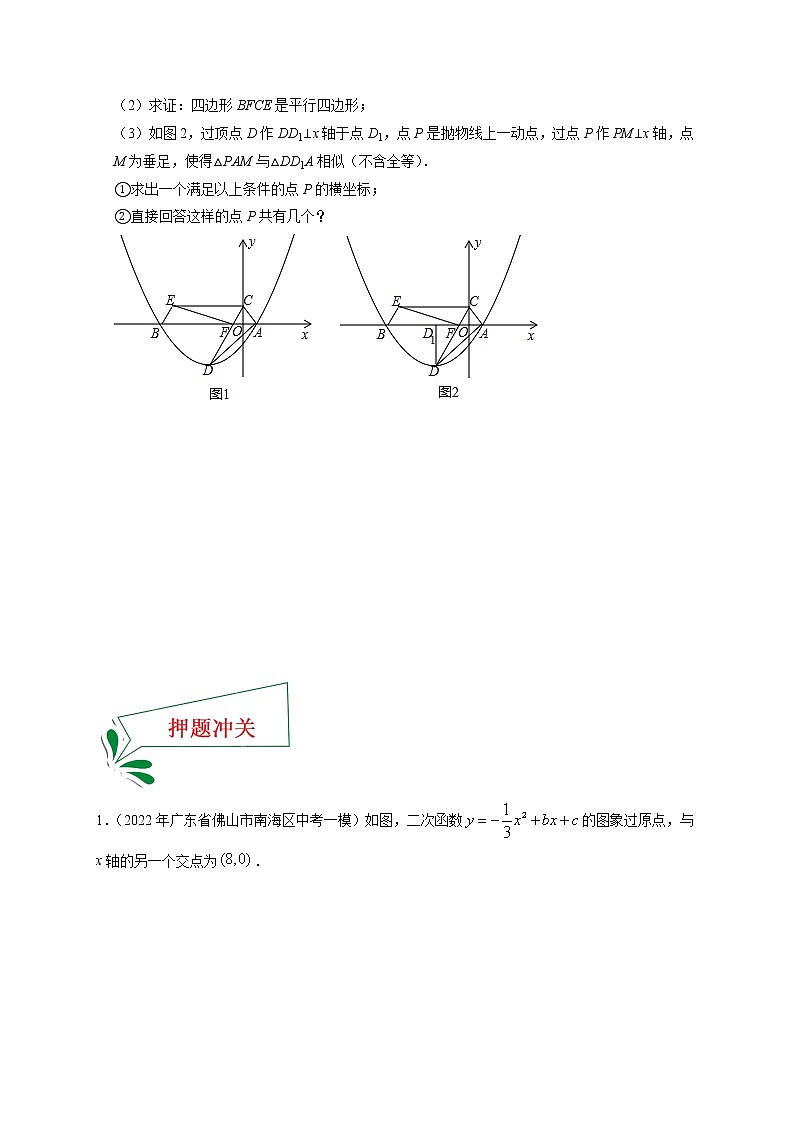
3．（2019广东）如图1，在平面直角坐标系中，抛物线y＝x2+x﹣与x轴交于点A、B（点A在点B右侧），点D为抛物线的顶点，点C在y轴的正半轴上，CD交x轴于点F，△CAD绕点C顺时针旋转得到△CFE，点A恰好旋转到点F，连接BE．

（1）求点A、B、D的坐标；

（2）求证：四边形BFCE是平行四边形；

（3）如图2，过顶点D作DD1⊥x轴于点D1，点P是抛物线上一动点，过点P作PM⊥x轴，点M为垂足，使得△PAM与△DD1A相似（不含全等）．

①求出一个满足以上条件的点P的横坐标；

②直接回答这样的点P共有几个？

1．（2022年广东省佛山市南海区中考一模）如图，二次函数的图象过原点，与x轴的另一个交点为．

（1）求该二次函数的解析式；

（2）在x轴上方作x轴的平行线，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．矩形ABCD为正方形，求m的值；

（3）在（2）的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒（），过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，当以A、E、F、Q四点为顶点构成的四边形为平行四边形时，请求出t的值．

2．（2022年广东省佛山市禅城区中考一模）函数y＝x2+bx+c图象交x轴于A，B两点（点A在左侧）、交y轴交于点C．已知：OB＝2OA，点F的坐标为（0，2），△AFB≌△ACB．

（1）求抛物线解析式；

（2）抛物线上点P在第一象限，当∠OCB＝2∠PCB时，求点P的坐标；

（3）抛物线上的点D在第一象限内，过点D作直线DE⊥x轴于点E，当7OE＝20DE时，直接写出点D的坐标；若点M在抛物线上，点N在抛物线的对称轴上，是否存在以点B，D，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．

3．（2022年广东省广州市黄埔区中考一模）已知抛物线y＝ax2＋bx＋3经过点和点，与y轴交于点C，P为第二象限内抛物线上一点．

（1）求抛物线的解析式，并写出顶点坐标；

（2）如图，连接PB，PO，PC，BC，OP交BC于点D，当S△CPD：S△BPD＝1：2时，求出点D的坐标．

4．（2022年广东省佛山市南海区中考二模）已知二次函数yx2＋bx＋c的图象与x轴交于A（1，0）和B（-3，0），与y轴交于点C．

（1）求该二次函数的表达式．

（2）如图1，连接BC，动点D以每秒1个单位长度的速度由A向B运动，同时动点E以每秒个单位长度的速度由B向C运动，连接DE，当点E到达点C的位置时，D、E同时停止运动，设运动时间为t秒．当△BDE为直角三角形时，求t的值．

（3）如图2，在抛物线对称轴上是否存在一点Q，使得点Q到x轴的距离与到直线AC的距离相等，若存在，求出点Q的坐标；若不存在，请说明理由．

5．（2022年广东省广州市增城区九年级中考一模）已知抛物线的顶点为．

（1）当时，求点的坐标；

（2）经过探究发现，随着的变化，顶点在某直线上运动，直线与轴，轴分别交于，两点，求的面积；

（3）若抛物线与直线的另一交点为，以为直径的圆与坐标轴相切，求的值．

1．（2022年广东省肇庆市四会市九年级下学期中考数学一模）如图，已知二次函数y＝x2+bx+c的图象经过A，B两点，BC⊥x轴于点C，且点A（﹣1，0），C（4，0），AC＝BC．

（1）求抛物线的解析式；

（2）点E是线段AB上一动点（不与A，B重合），过点E作x轴的垂线，交抛物线于点F，当线段EF的长度最大时，求点E的坐标及S△ABF；

（3）点P是抛物线对称轴上的一个动点，是否存在这样的P点，使△ABP成为直角三角形？若存在，直接写出所有点P的坐标；若不存在，请说明理由．

2．（2022年广东省肇庆市高要区中考一模）如图所示，在平面直角坐标系中，抛物线经过、、三点，其顶点为，连接，点是线段上一个动点（不与、重合），过点作轴的垂线，垂足点为，连接．

（1）求抛物线的函数解析式，并写出顶点的坐标：

（2）如果点的坐标为，的面积为，求与之间的函数关系式，直接写出自变量的取值范围，并求出的最大值；

3．（汕尾市2021-2022学年度义务教育学业质量监测九年级二模）如图①，抛物线与轴负半轴交于点，与轴的另一交点为，与轴正半轴交于点，抛物线的对称轴与直线相交于点，与轴交于点．

（1）求抛物线的解析式及对称轴；

（2）抛物线的对称轴上存在点，使得，利用图①求点的坐标；

（3）如图②，抛物线的对称轴与抛物线相交于点，连接，在抛物线上是否存在点（不与点重合），使得？若存在，请直接写出点的坐标；若不存在，请说明理由．

4．（2022年广东省梅州市中考数学1模）如图，在平面直角坐标系中，抛物线的顶点坐标为，与轴交于点，与交于点，．

（1）求二次函数的表达式；

（2）过点作平行于轴，交抛物线于点，点为抛物线上的一点（点在上方），作平行于轴交于点，当点在何位置时，四边形的面积最大？求出最大面积；

（3）若点在抛物线上，点在其对称轴上，以，，，为顶点的四边形是平行四边形，且为其一边，求点的坐标．

5．（2022年广东省珠海市九年级下学期数学第二次模拟）如果抛物线C1的顶点在抛物线C2上，抛物线C2的顶点也在抛物线C1上时，那么我们称抛物线C1与C2“互为关联”的抛物线．如图1，已知抛物线C1：y1＝x2+x与C2：y2＝ax2+x+c是“互为关联”的抛物线，点A，B分别是抛物线C1，C2的顶点，抛物线C2经过点D（6，﹣1）．

（1）直接写出A，B的坐标和抛物线C2的解析式；

（2）抛物线C2上是否存在点E，使得△ABE是直角三角形？如果存在，请求出点E的坐标；如果不存在，请说明理由；

（3）如图2，点F（﹣6，3）在抛物线C1上，点M，N分别是抛物线C1，C2上的动点，且点M，N的横坐标相同，记△AFM面积为S1（当点M与点A，F重合时S1＝0），△ABN的面积为S2（当点N与点A，B重合时，S2＝0），令S＝S1+S2，观察图象，当y1≤y2时，写出x的取值范围，并求出在此范围内S的最大值．

7．（2022年广东省中山市纪中、纪雅、三鑫三校联考中考数学一模）如图，拋物线与x轴交于A，B两点（点A在点B的左侧），顶点为D．点P为对称轴右侧抛物线上的一个动点，其横坐标为m，直线AD交y轴于点C，过点P作PF∥AD交x轴于点．F，PE∥x轴，交直线AD于点E，交直线DF于点M．

（1）求直线AD的表达式及点C的坐标；

（2）当DM＝3MF时，求m的值；

（3）试探究点P在运动过程中，是否存在m，使四边形AFPE是菱形，若存在，请直接写出点P的坐标；若不存在，请说明理由．

8．（2021汕头市金平区一模）如图1，直线y＝﹣x+2与x轴交于点B，与y轴交于点C，抛物线y＝﹣x2+bx+c经过B、C两点，点P是抛物线上的一个动点，过点P作PQ⊥x轴，垂足为Q，交直线y＝﹣x+2于点D．设点P的横坐标为m．

（1）求该抛物线的函数表达式；

（2）若以P、D、O、C为顶点的四边形是平行四边形，求点Q的坐标；

（3）如图2，当点P位于直线BC上方的抛物线上时，过点P作PE⊥BC于点E，求当PE取得最大值时点P的坐标，并求PE的最大值．

9.（2021佛山市大沥镇一模） 如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N，其项点为D．

（1）填空：抛物线的解析式为　   　；

（2）若P是抛物线上位于直线AC上方的一个动点，设点P的横坐标为t，过点P作y轴的平行线交AC与M，当t为何值时，线段PM的长最大，并求其最大值；

（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，请直接写出点E的坐标；若不能，请说明理由．

10．（2021佛山市禅城区一模）如图，抛物线y＝﹣x2+x+3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ．过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E，连接PD，与BC交于点F．设点P的运动时间为t秒（t＞0）．

（1）求直线BC的函数表达式；

（2）①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）

②在点P、Q运动的过程中，当PQ＝PD时，求t的值；

（3）试探究在点P，Q运动的过程中，是否存在某一时刻，使得点F为PD的中点？若存在，请直接写出此时t的值与点F的坐标；若不存在，请说明理由．