新教材2023年高中数学章末知识梳理2第2章圆锥曲线课件北师大版选择性必修第一册

这是一份新教材2023年高中数学章末知识梳理2第2章圆锥曲线课件北师大版选择性必修第一册，共25页。

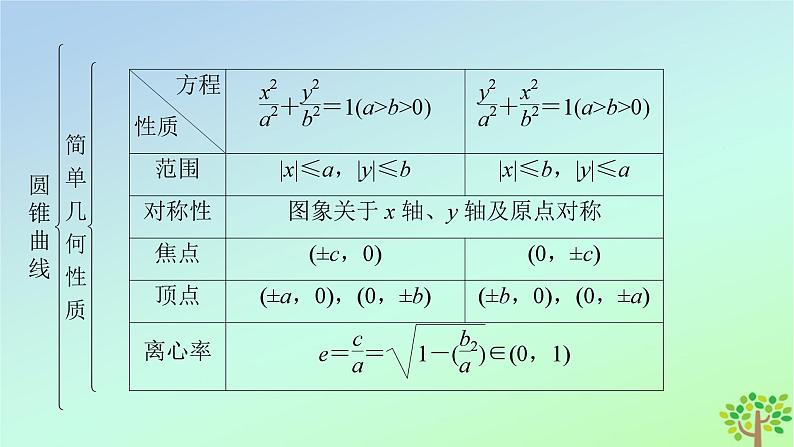
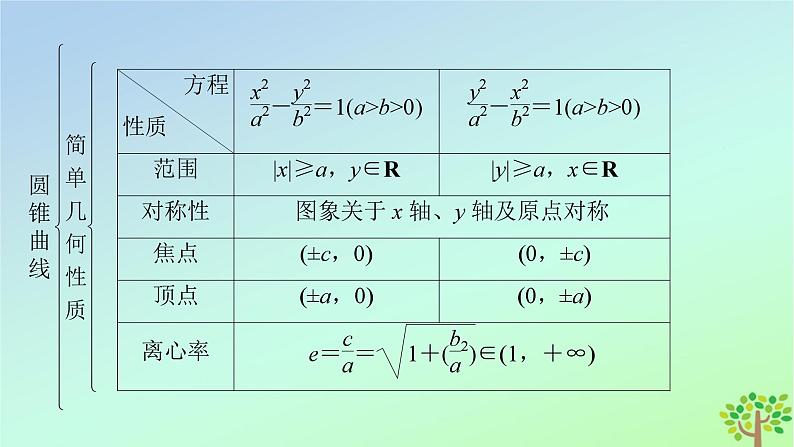
第二章　圆锥曲线章末知识梳理知识体系构建圆锥曲线圆锥曲线圆锥曲线圆锥曲线圆锥曲线圆锥曲线圆锥曲线要点专项突破求动点的轨迹方程，实质是建立动点的坐标(x，y)间的关系f(x，y)＝0，解题的关键是认真分析形成轨迹的动点与已知条件的内在联系，选择恰当的方法构建动点的轨迹方程．探求动点轨迹问题的常用方法有：直接法、定义法、相关点法、交轨法． 在平面直角坐标系xOy中，已知点F(1，0)，直线l：x＝－1，点P在直线l上移动，R是线段PF与y轴的交点，动点Q满足RQ⊥PF，PQ⊥l.求动点Q的轨迹方程E.典例1当动点所满足的条件恰符合某曲线的定义时，如到定点的距离等于定长，或到两定点距离之和等于定值(且大于两定点之距)，或到两定点距离之差的绝对值等于定值(且小于两定点之距)等，常利用定义法确定动点的轨迹，结合已知条件求出基本量即得动点的轨迹方程． 求解下列问题．(1)已知圆M：(x＋1)2＋y2＝1，圆N：(x－1)2＋y2＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C，求C的方程．(2)已知两个定圆O1和O2，它们的半径分别是1和2，且|O1O2|＝4，动圆M与圆O1内切，且与圆O2外切，建立适当的坐标系，求动圆圆心M的轨迹方程，并说明轨迹是何种曲线．典例2(2)如图，以O1O2的中点O为原点，O1O2所在直线为x轴建立平面直角坐标系．由|O1O2|＝4，得点O1(－2，0)，O2(2，0)．设动圆M的半径为r，则由动圆M与圆O1内切，有|MO1|＝r－1；由动圆M与圆O2外切，有|MO2|＝r＋2.所以|MO2|－|MO1|＝3<|O1O2|＝4.典例3当动点是两动曲线的交点时，常采用交轨法求动点轨迹方程，即引入变量表示两条动曲线的方程，将两曲线方程联立为方程组并消去变量，所得x，y的方程即为动点的轨迹方程． A，B是抛物线y2＝4ax(a>0)上的两动点，且OA⊥OB，OP⊥AB，垂足为点P，求动点P的轨迹．典例4