






还剩26页未读,
继续阅读
成套系列资料,整套一键下载
高中北师大版 (2019)第一章 直线与圆2 圆与圆的方程2.3 直线与圆的位置关系说课ppt课件
展开
这是一份高中北师大版 (2019)第一章 直线与圆2 圆与圆的方程2.3 直线与圆的位置关系说课ppt课件,共34页。PPT课件主要包含了§2圆与圆的方程,必备知识·探新知,知识点,直线与圆的位置关系,关键能力·攻重难,典例1,典例2,典例3,典例4,课堂检测·固双基等内容,欢迎下载使用。
2.3 直线与圆的位置关系
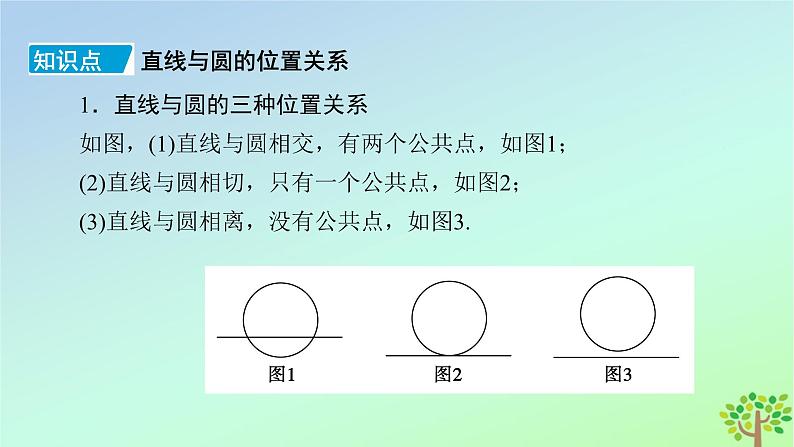
1.直线与圆的三种位置关系如图,(1)直线与圆相交,有两个公共点,如图1;(2)直线与圆相切,只有一个公共点,如图2;(3)直线与圆相离,没有公共点,如图3.
2.判断直线与圆的位置关系的两种方法方法1(代数法):判断直线l的方程与圆C的方程组成的方程组是否有实数解.如果有实数解,那么直线l与圆C有公共点;如果没有实数解,那么直线l与圆C没有公共点.当有两组不同的实数解时,直线l与圆C相交;当只有一组实数解时,直线l与圆C相切;当无实数解时,直线l与圆C相离.
方法2(几何法):判断圆C的圆心到直线l的距离d与圆C的半径r的大小关系.直线l与圆C相交⇔dr.
已知直线l:3x+y-6=0和圆C:x2+y2-2y-4=0,判断直线l与圆C的位置关系.
[规律方法] 1.几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.2.代数法:根据直线方程与圆的方程组成的方程组解的个数来判断.3.直线系法:若直线恒过定点,可通过判断定点与圆的位置关系来判断直线与圆的位置关系.但有一定的局限性,必须是过定点的直线系.
【对点训练】❶ 求实数m的取值范围,使直线x-my+3=0与圆x2+y2-6x+5=0分别满足:①相交;②相切;③相离.
[规律方法] 1.几何法:设出切线方程,利用圆心到直线的距离等于半径,求出未知量,此种方法需要注意斜率不存在的情况,要单独验证,若符合题意,则直接写出切线方程.2.代数法:设出切线方程后与圆的方程联立消元,利用判别式等于零,求出未知量,若消元后的方程为一元一次方程,则说明要求的切线中,有一条切线的斜率不存在,可直接写出切线方程.3.设切点坐标:先利用切线的性质解出切点坐标,再利用直线的两点式写出切线方程.
【对点训练】❷ 若直线l过点P(2,3),且与圆C:(x-1)2+(y+2)2=1相切,求直线l的方程.[分析] 先确定点P在圆C外,再对切线l的斜率是否存在进行分类讨论,利用待定系数法求直线方程.
由b=2x+y,知b表示直线2x+y-b=0在y轴上的截距,如图2所示.
[规律方法] 1.与圆有关的最值问题,可借助几何特征及几何法先确定达到最值的位置,再进行计算.有些与圆有关的最值问题涉及是否过圆心,有时注意考虑表达式中字母的几何意义,如两点间距离公式、斜率公式、在y轴上的截距等.2.对于本题而言,解决的关键是理解m和b的几何意义,同时要借助分界线探求参数的取值范围.
忽略直线斜率是否存在导致漏解已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,则直线l的方程为________________________.
x=-4或4x+3y+25=0
[辨析] 误认为直线斜率一定存在,直接设为k.
1.直线3x+4y-25=0与圆x2+y2=9的位置关系为( )A.相切 B.相交C.相离 D.相离或相切2.对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系一定是( )A.相离 B.相切C.相交但直线不过圆心 D.相交且直线过圆心[解析] 直线y=kx+1恒过定点(0,1),由定点(0,1)在圆x2+y2=2内,知直线y=kx+1与圆x2+y2=2一定相交.又直线y=kx+1不过圆心(0,0),则位置关系是相交但直线不过圆心,故选C.
3.若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是( )A.[-3,-1] B.[-1,3]C.[-3,1] D.(-∞,-3]∪[1,+∞)
4.已知直线l:mx+y-3=0与圆(x-1)2+(y-2)2=4交于A,B两点,过A,B分别做l的垂线与x轴交于C,D两点,若|AB|=4,则|CD|=______.
2.3 直线与圆的位置关系
1.直线与圆的三种位置关系如图,(1)直线与圆相交,有两个公共点,如图1;(2)直线与圆相切,只有一个公共点,如图2;(3)直线与圆相离,没有公共点,如图3.
2.判断直线与圆的位置关系的两种方法方法1(代数法):判断直线l的方程与圆C的方程组成的方程组是否有实数解.如果有实数解,那么直线l与圆C有公共点;如果没有实数解,那么直线l与圆C没有公共点.当有两组不同的实数解时,直线l与圆C相交;当只有一组实数解时,直线l与圆C相切;当无实数解时,直线l与圆C相离.
方法2(几何法):判断圆C的圆心到直线l的距离d与圆C的半径r的大小关系.直线l与圆C相交⇔d
已知直线l:3x+y-6=0和圆C:x2+y2-2y-4=0,判断直线l与圆C的位置关系.
[规律方法] 1.几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.2.代数法:根据直线方程与圆的方程组成的方程组解的个数来判断.3.直线系法:若直线恒过定点,可通过判断定点与圆的位置关系来判断直线与圆的位置关系.但有一定的局限性,必须是过定点的直线系.
【对点训练】❶ 求实数m的取值范围,使直线x-my+3=0与圆x2+y2-6x+5=0分别满足:①相交;②相切;③相离.
[规律方法] 1.几何法:设出切线方程,利用圆心到直线的距离等于半径,求出未知量,此种方法需要注意斜率不存在的情况,要单独验证,若符合题意,则直接写出切线方程.2.代数法:设出切线方程后与圆的方程联立消元,利用判别式等于零,求出未知量,若消元后的方程为一元一次方程,则说明要求的切线中,有一条切线的斜率不存在,可直接写出切线方程.3.设切点坐标:先利用切线的性质解出切点坐标,再利用直线的两点式写出切线方程.
【对点训练】❷ 若直线l过点P(2,3),且与圆C:(x-1)2+(y+2)2=1相切,求直线l的方程.[分析] 先确定点P在圆C外,再对切线l的斜率是否存在进行分类讨论,利用待定系数法求直线方程.
由b=2x+y,知b表示直线2x+y-b=0在y轴上的截距,如图2所示.
[规律方法] 1.与圆有关的最值问题,可借助几何特征及几何法先确定达到最值的位置,再进行计算.有些与圆有关的最值问题涉及是否过圆心,有时注意考虑表达式中字母的几何意义,如两点间距离公式、斜率公式、在y轴上的截距等.2.对于本题而言,解决的关键是理解m和b的几何意义,同时要借助分界线探求参数的取值范围.
忽略直线斜率是否存在导致漏解已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,则直线l的方程为________________________.
x=-4或4x+3y+25=0
[辨析] 误认为直线斜率一定存在,直接设为k.
1.直线3x+4y-25=0与圆x2+y2=9的位置关系为( )A.相切 B.相交C.相离 D.相离或相切2.对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系一定是( )A.相离 B.相切C.相交但直线不过圆心 D.相交且直线过圆心[解析] 直线y=kx+1恒过定点(0,1),由定点(0,1)在圆x2+y2=2内,知直线y=kx+1与圆x2+y2=2一定相交.又直线y=kx+1不过圆心(0,0),则位置关系是相交但直线不过圆心,故选C.
3.若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是( )A.[-3,-1] B.[-1,3]C.[-3,1] D.(-∞,-3]∪[1,+∞)
4.已知直线l:mx+y-3=0与圆(x-1)2+(y-2)2=4交于A,B两点,过A,B分别做l的垂线与x轴交于C,D两点,若|AB|=4,则|CD|=______.













