初中数学苏科版八年级上册2.5 等腰三角形的轴对称性优秀课件ppt

这是一份初中数学苏科版八年级上册2.5 等腰三角形的轴对称性优秀课件ppt，共18页。PPT课件主要包含了等腰三角形的性质，等腰三角形判定定理，课后回顾等内容，欢迎下载使用。

性质1 等腰三角形的两个底角相等（简写成“等边对等角”）
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（可简记为“三线合一”）
性质3 等腰三角形是轴对称图形。
学习目标1、探索等腰三角形判定定理。2、理解等腰三角形的判定定理，并会运用其进行简单的证明。重点等腰三角形的判定定理及应用。难点能运用等腰三角形的判定定理解决实际问题，并能灵活运用。
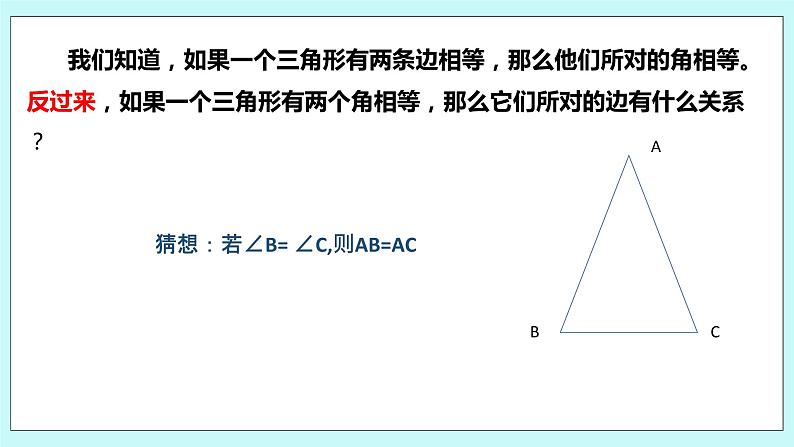
我们知道，如果一个三角形有两条边相等，那么他们所对的角相等。反过来，如果一个三角形有两个角相等，那么它们所对的边有什么关系？
猜想：若∠B= ∠C,则AB=AC
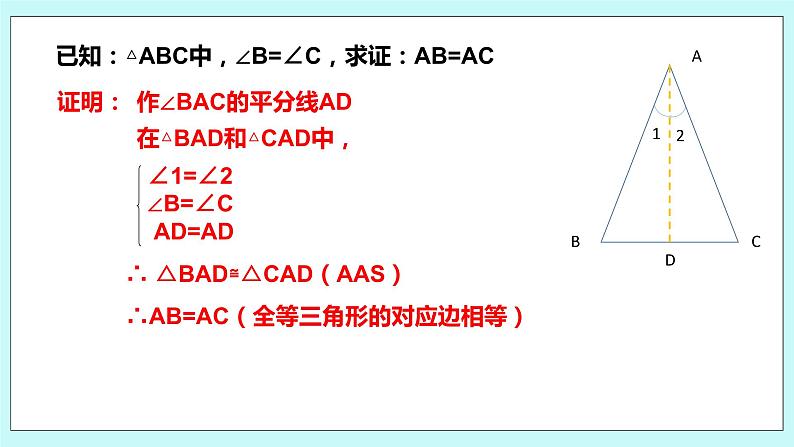
已知：△ABC中，∠B=∠C，求证：AB=AC
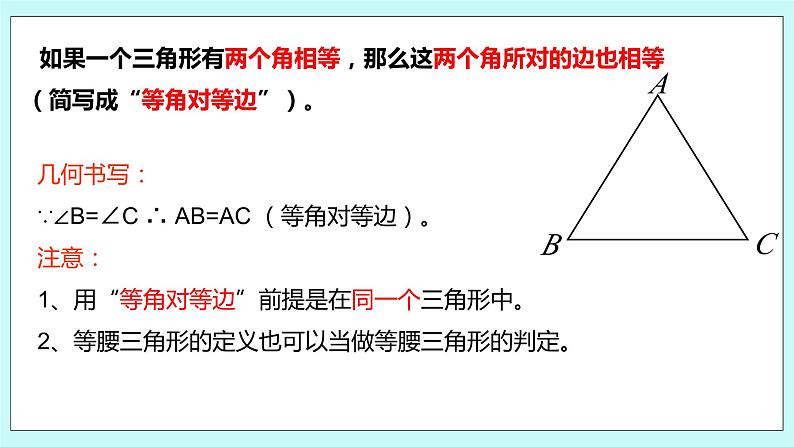
如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）。
几何书写： ∵∠B=∠C ∴ AB=AC （等角对等边）。注意：1、用“等角对等边”前提是在同一个三角形中。2、等腰三角形的定义也可以当做等腰三角形的判定。
等腰三角形的性质定理与判定定理有什么区别?
性质定理：等边对等角。判定定理：等角对等边。
等边 等角
等角 等边
1.求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形。
已知： 如图，∠CAE是△ABC的外角，∠1=∠2，AD∥BC，求证：AB=AC
2.如图，在△ABC和△DCB中，∠A＝∠D＝72°，∠ACB＝∠DBC＝36°，则图中等腰三角形的个数是( ) A．2 B．3 C．4 D．5
【详解】∵∠ACB＝∠DBC＝36°， ∴∠AOB＝∠DOC＝∠ACB＋∠DBC＝72°，∵∠A＝∠D＝72°，∴∠ABD＝∠DCA＝180°−72°−72°＝36°，即∠A＝∠AOB、∠A＝∠ABC、∠OBC＝∠OCB、∠D＝∠DOC、∠D＝∠DCB，∴△ABO、△ABC、△OBC、△DCO、△DBC都是等腰三角形.故答案选：D．
3.已知：如图，AD ∥BC，BD平分∠ABC，求证：AB=AD
证明：∵ AD ∥BC ∴∠ADB=∠DBC∵ BD平分∠ABC∴ ∠ABD=∠DBC∵∠ABD=∠DBC，∠ADB=∠DBC∴∠ABD=∠ADB∴AB=AD（等角对等边）
4.如图，AC和BD相交于点O，且AB∥DC，OA=OB，求证：OC=OD．
1．如图，已知每个小方格的边长为1，A、B两点都在小方格的格点（顶点）上，请在图中找一个格点C，使△ABC是等腰三角形，这样的格点C有________个。
2．如图，在△ABC中， AB=AC， ∠A=36° ，BD、CE分别是∠ABC、∠BCD 的角平分线，则图中的等腰三角形有 （ ）A．5个B．1个C．3个D．2个
3．如图，在△ABC中，∠C＝90°，AC＝BC，AD是∠BAC的平分线，DE⊥AB于E，1）若CD＝1cm，求AC的长；2）求证：AB=AC+CD．
4．如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
4．如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
(2)∵∠COF=∠FCO,∴OF=CF.∵∠BOE=∠OBE,∴OE=BE.∴△AEF的周长=AF+OF+OE+AE=AF+CF+BE+AE=AB+AC=8 cm.∴△ABC的周长=8+4=12(cm).
等腰三角形判定定理的证明
等腰三角形判定定理的应用